Введение
Экспоненциальная линия как класс неоднородных линий передач широко используется во множестве различных устройств СВЧ техники [8]. Также она может найти применение в радиоэлектронных системах как трансформатор импеданса, в цепях согласования, фильтрах и т. д [1,5,6,9]. Эта линия имеет преимущества, когда используется как трансформатор импеданса в широкой полосе частот, а также позволяет проектировать большую полосу заграждения в фильтах.
В статьях [3,4,10] была рассмотрена экспоненциальная линия с равномерными и малыми потерями в проводнике по всей длине. Цель представленной работы – исследование диссипативных характеристик экспоненциальной линии в широкой полосе частот. Рассматриваются два случая, первый – когда проводимость на единицу длины постоянна вдоль длины линии, второй – проводимость на единицу длины изменяется экспоненциально.
Обзор решения методом теории возмущений
Рассматривается неоднородная линия передачи длиной d. Линия присоединена к генератору напряжения E с одного конца, а с другого – к линии с потерями с импедансом Z0, как показано на рис.1.
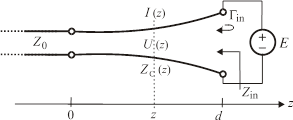
Рисунок 1. Схема неоднородной линии передачи
Для TEM моды, напряжением ![]() , и током
, и током ![]() , распространяющейся вдоль линии, можно определить точное решение следующих дифференциальных уравнений.
, распространяющейся вдоль линии, можно определить точное решение следующих дифференциальных уравнений.
![]() ,
, ![]() (1)
(1)
Импеданс и адмитанс в цепи:
![]()
![]() (2)
(2)
где w – круговая частота, а ![]() ,
, ![]() ,
, ![]() и
и ![]() это сопротивление, индуктивность, проводимость и ёмкость на единицу длины линии, соответственно. Импеданс линии:
это сопротивление, индуктивность, проводимость и ёмкость на единицу длины линии, соответственно. Импеданс линии:
![]() (3)
(3)
Выражения (1) и могут быть преобразованы в выражения второго порядка для напряжений и токов. Дифференциальное выражение для напряжения:
![]() (4)
(4)
где ![]() ,
, ![]() . (5)
. (5)
Выражение (4) решается с граничными условиями: ![]() и
и ![]() (6)
(6)
Если функции![]() и
и ![]() постоянны, то
постоянны, то ![]() и
и ![]() , и уравнение (4) может быть решено аналитически. В этом случае решение записывается:
, и уравнение (4) может быть решено аналитически. В этом случае решение записывается:
![]() (7)
(7)
где ![]() ,
, ![]() ,
, 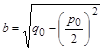 (8)
(8)
Постоянные![]() and
and ![]() можно определить исходя из граничных условий (6):
можно определить исходя из граничных условий (6):
![]() и
и ![]() (9)
(9)
В общем случае, когда линия передачи неоднородна, функции![]() и
и ![]() будут:
будут:
![]() (10)
(10)
и ![]() . (11)
. (11)
Таким образом, запишем (4) в виде: ![]() (12)
(12)
где ![]() (13)
(13)
Решение выражения (12) может быть определено методом вариаций [2] в форме:
![]() (14)
(14)
где 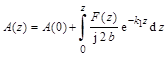 и
и 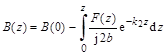 . (15)
. (15)
Постоянные ![]() и
и ![]() могут быть определены исходя из граничных условий (6). Заметим, что для z=0 удовлетворяется следующее условие:
могут быть определены исходя из граничных условий (6). Заметим, что для z=0 удовлетворяется следующее условие:
![]() . (16)
. (16)
Постоянные ![]() и
и ![]() могут быть записаны в аналогично (9):
могут быть записаны в аналогично (9):
![]() и
и ![]() (17)
(17)
где ![]() ,
, ![]() ,
, ![]() (18)
(18)
Наконец, в соответствии с выражением (14), используя выведенные выше выражения, находим напряжение ![]() в требуемых сечениях z.
в требуемых сечениях z.
Метод возмущений может быть использован во многих случаях, когда требуется получить более точное решение выражения (14) для напряжений, также, более точную аппроксимацию для F(z) можно получить, используя выражение (12).
Экспоненциальная линия с постоянным распределением проводимости по длине
Во-первых, рассмотрим потери в экспоненциальной линии передачи. Потерями в проводнике линии передачи можно пренебречь (![]() ), пока проводимость
), пока проводимость ![]() постоянна вдоль линии. В этом случае экспоненциальная линия передачи имеет следующие распределённые параметры:
постоянна вдоль линии. В этом случае экспоненциальная линия передачи имеет следующие распределённые параметры:
![]()
![]() (19)
(19)
где ![]() ,
, ![]() и
и ![]() соответственно индуктивность, ёмкость и импеданс на модуль длины в точке z = 0 линии. Здесь a – это коэффициент конусности
соответственно индуктивность, ёмкость и импеданс на модуль длины в точке z = 0 линии. Здесь a – это коэффициент конусности
![]() , (20)
, (20)
который может быть положительным, нулевым или отрицательным, а ![]() – это значение импеданса в точке
– это значение импеданса в точке ![]()
![]() . В этом случае коэффициенты
. В этом случае коэффициенты ![]() и
и ![]() в выражении (4):
в выражении (4):
![]() и
и ![]() (21)
(21)
где ![]() и
и ![]() (22)
(22)
где ![]() это постоянная
это постоянная ![]() . (23)
. (23)
На первом этапе расчётов возмущениями в линии пренебрегают ![]() в этом случае напряжения вдоль линии вычисляются выражением (7). Следующий шаг – это определить функцию
в этом случае напряжения вдоль линии вычисляются выражением (7). Следующий шаг – это определить функцию ![]() , когда возмущение будет малым. В таком случае выражение (15) будет:
, когда возмущение будет малым. В таком случае выражение (15) будет:
![]() (24)
(24)
где ![]() (25)
(25)
Решение выражения (32) получают через (7), где
![]() и
и ![]() . (26)
. (26)
Это имеет значение для случая, когда применяется метод возмущений. Постоянные ![]() и
и ![]() находим через (17), где
находим через (17), где
![]() и
и ![]() . (27)
. (27)
Когда напряжение известно, токи в линии можно найти через (1)
![]()
![]() (28)
(28)
где ![]() и
и ![]() . (29)
. (29)
Линия передачи с экспоненциальным распределением проводимости по длине
Во втором случае проводимость диэлектрика s будет постоянной, шунтирующая её проводимость металла на единицу длины будет изменяться экспоненциально, а импеданс:
![]() , (30)
, (30)
где e – диэлектрическая проницаемость. В таком случае, адмитанс запишем в форме:
![]() (31)
(31)
коэффициент p(z) находим из (27), а q(z) будет:
![]() (32)
(32)
Далее, дифференциальное выражение для напряжения линии аналогично (24), но с отличной функцией F(z), имеющей форму:
![]() (33)
(33)
В случае диэлектрика с малыми потерями можно принять, что ![]() , выражение (24) может быть решено по аналогии с предыдущим примером расчёта, когда проводимость на единицу длины была постоянна, используя метод возмущений.
, выражение (24) может быть решено по аналогии с предыдущим примером расчёта, когда проводимость на единицу длины была постоянна, используя метод возмущений.
Также, напряжения могут быть найдены из выражения (14), а необходимые выражения, как и в предыдущем случае, для A(z) и B(z) будут отличаться от (26):
![]() ,
, ![]() . (34)
. (34)
Данные расчётов
Рассмотрим случай, когда ![]()
![]()
![]() ,
, ![]() . Примем
. Примем ![]() , а
, а ![]() .
.
Входной импеданс в сечении z = d определяется как:
![]() , (35)
, (35)
коэффициент отражения от входа: ![]() . (36)
. (36)
Коэффициент стоячей волны напряжения (КСВН): ![]() . (37)
. (37)
Относительное распределение импеданса вдоль линии передачи как функция z/l для нескольких значений проводимости на единицу длины G¢ представлена на рис. 2. Полученные результаты показывают, что величина изменения импеданса как функции проводимости на единицу длины тем больше, чем больше величина проводимости.
Рис. 3 показывает зависимость КСВН входа (VSWR) в зависимости от отношения d/l для различных значений величины проводимости G¢. Значение входного импеданса и коэффициента отражения, полученные с помощью метода возмущений для нескольких постоянных значений проводимости G¢, приведены в табл. 1. Расчёты проведены для случая, когда проводимость на единицу длины G¢ изменяется экспоненциально.
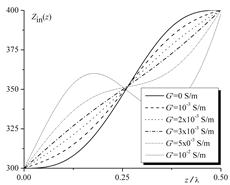
Рисунок 2. Входной импеданс для разных значений проводимости G¢
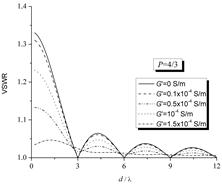
Рисунок 3. КСВН входа в зависимости от значения величины проводимости G¢
Таблица 1. Значения входного импеданса и коэффициента отражения от G¢
|
G’[S/m] |
|
|
G’[S/m] |
|
|
|
10-3 |
400.269+j6.380 |
0.007979 |
3x10-3 |
399.955+j19.150 |
0.023932 |
|
2x10-3 |
400.214+j12.767 |
0.015954 |
5x10-3 |
398.828+j31.866 |
0.039887 |
Зависимость КСВН входа для нескольких значений коэффициента передачи P, где P = Zd/Z0 , показана на рис. 4, для диэлектрика с проводимостью 10-3 S/m.
Как видно из полученных результатов, характеристики трансформатора ухудшаются при увеличении потерь в диэлектрике. Рис. 5 показывает зависимость КСВН от длины волны или частоты, для нескольких значений проводимости диэлектрика. Видно, что характеристики трансформации экспоненциальной линии ухудшаются при увеличении проводимости, что более выражено на низких частотах.
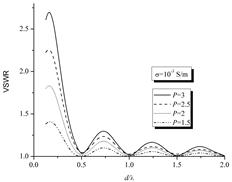
Рисунок 4. КСВН входа в зависимости от значения коэффициента передачи P
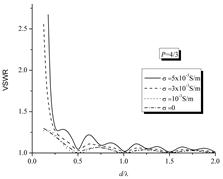
Рисунок 5. КСВН в зависимости от d/l для нескольких значений проводимости s
В таблице 2 приведены результаты входного импеданса и КСВН, полученные методом возмущений [1], сравниваются для нескольких значений длин волн для случая неидеального диэлектрика с проводимостью s = 10-3 S/m.
Таблица 2. Входной импеданс и КСВН в зависимости от длины волны
|
l[m] |
Zul [W] |
VSWR |
l[m] |
Zul [W] |
VSWR |
|
0.5 |
399.989+j1.726 |
1.004325 |
0.875 |
401.741-j4.698 |
1.012576 |
|
0.625 |
398.642-j22.144 |
1.057123 |
1.0 |
399.959+j3.462 |
1.008693 |
|
0.75 |
401.049-j22.493 |
1.057822 |
1.125 |
398.636-j1.198 |
1.004557 |
Заключение
Из полученных данных можно заключить, что передаточные характеристики линии ухудшаются, если значение проводимости диэлектрика, либо проводимость на единицу длины увеличивается. Использование экспоненциальной линии для согласования или преобразования импедансов, в рассмотренном частном случае, ограничено частотным диапазоном и длиной линии передачи. Расчётные данные подтверждают, что экспоненциальная линия передачи с относительно малыми потерями в диэлектрике является хорошим широкополосным трансформатором импедансов. Данную методику расчёта можно использовать при расчёте линии передачи с неоднородным или магнитоэлектрическим заполнением [7] и в дальнейшем применить для расчёта сложных СВЧ устройств.
Работа выполнена в рамках реализации федеральной целевой программы «Научные и научно-педагогические кадры инновационной России» на 2009–2013 годы.
Рецензенты:
Захаров Анатолий Юльевич, д.ф.-м.н., профессор, заведующий секцией кафедры общей и экспериментальной физики Института электронных и информационных систем, г. Великий Новгород.
Корнышев Николай Петрович, д.т.н., доцент, ведущий научный сотрудник НИИ ПТ «РАСТР», г. Великий Новгород.
Библиографическая ссылка
Цветкович З. З., Алексич С. Р., Бажич М. И., Татаренко А. С., Бритин С. Н., Бичурин М. И., Петров Р. В. ЛИНИЯ ПЕРЕДАЧИ С КОНЕЧНЫМИ ПОТЕРЯМИ В ДИЭЛЕКТРИКЕ // Современные проблемы науки и образования. 2012. № 6. ;URL: https://science-education.ru/ru/article/view?id=7720 (дата обращения: 29.01.2026).



