Теория управления объектами с распределенными параметрами стала разрабатываться уже после того, как были получены основные результаты в теории оптимизации для обыкновенных дифференциальных уравнений [1] и в отличие от последней, имеет гораздо менее завершенный характер. Это связано с трудностью исследования уравнений в частных производных, при наличии сложных граничных и начальных условий, а также с усложнением характера дополнительных ограничений, вызванных конкретными практическими постановками задач.
В настоящее время есть много работ, освещающих те или иные проблемы теории оптимального управления объектами, состояние которых описывается дифференциальными уравнениями в частных производных. Среди них: оптимальные задачи, вопросы существования и апроксимации оптимальных решений, управляемость, наблюдаемость и идентификация объектов, необходимые и достаточные условия оптимальности процесса и др.
В данной работе исследуется вопрос о точечной полноте систем уравнений в частных производных гиперболического типа.
Понятие точечной полноты впервые было введено L. Weiss’ом, [3], который использовал его при исследовании управляемости систем с запаздыванием. До сих пор доказана точечная полнота линейных систем без запаздывания, при достаточно малом запаздывании [2] и др.
Пусть состояние объекта с распределенными параметрами описывается следующей системой уравнений в частных производных гиперболического типа:
(1)
где x - n вектор, характеризирующий состояние системы, 
постоянные матрицы, 
Для того, чтобы однозначно определить решение системы, зададим дополнительные условия типа Гурса на характеристиках 
и 
системы:
(2)
и условие согласованности:
Определение: Систему (1) – (2) назовем точечно полной, если для любого n - вектора p, 
¹ 0 и любых 
, 
, 
выполняется:
0
Попробуем найти условия, при которых система (1) – (2) будет точечно полной. Для этого сначала запишем решение системы в более компактном виде. Вводим неизвестную матричную функцию 
размерности 
, для которой предполагаем, что непрерывна по совокупности аргументов вместе с производными по 
и 
. Умножим систему (1) слева на и проинтегрируем в пределах от 0 до t и от 0 до s:
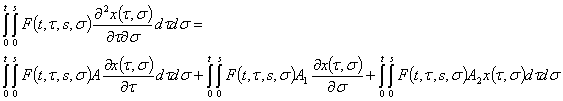
Применяя формулу интегрирования по частям и замены порядка интегрирования, преобразуем все интегралы в левой и правой части последнего равенства, после чего получаем:
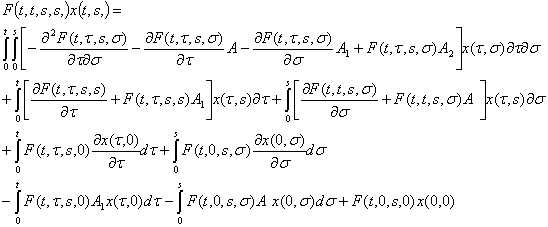
Поскольку функция 
неопределенная, потребуем от нее выполнения следующих условий:
(3)
(4)
, , (5)
где 
единичная матрица.
Сопряженная с системой (1) система (3), вместе с дополнительными условиями (4) на прямых и и условие (5) в точке 
полностью определяют функцию , которую по аналогии с математической физикой можно назвать матричной функцией Римана.
Теперь, учитывая (3) - (5), можем записать решение системы (1) - (2) в следующем компактном виде:
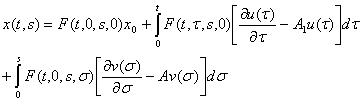(6)
Допустим теперь, что система (1) не является точечно полной. Тогда, согласно определению точечной полноты, существует n – вектор 
, что для любых 
, 
выполняется:
Имея ввиду (6) это условие запишется в виде:
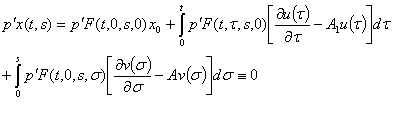(7)
Поскольку функции 
и 
произвольные, для выполнения (7) необходимо и достаточно выполнения следующих условий:
, 
(8)
, 
Обозначим теперь через 
вектор функцию:
Из формул (3) и (8) следует, что 
удовлетворяет следующему дифференциальному уравнению:
(9)
с дополнительными условиями на прямых 
и 
:
Поскольку (9) - однородное относительно функции 
, а начальные условия - нулевые, то следует, что:
для и (10)
Таким образом показали, что система (1) - (2) будет точечно неполной тогда и только тогда, когда существует n – вектор p, , что выполняется условие (10).
Допустим, что система (1) - (2) точечно неполная. Тогда существует вектор p, ,что выполняется в 
. Вычислим в точке , . Поскольку имеет место (10), то:
,
С другой стороны, согласно (5) имеем:
Выполнение последних двух равенств возможно лишь при условии, что 
. Это противоречит допущению, что . Таким образом доказали следующую теорему:
Теорема:
Система (1) - (2) точечно полная.
СПИСОК ЛИТЕРАТУРЫ:
1. Габасов Р., Ф.Кириллова. Качественная теория оптимальных процессов. Москва, „Наука”, 1971.
2. Зверкин А.М. О точечной полноте систем с запаздыванием. // Дифференциальные уравнения. 1973, том IX, №3
3. Weiss, L. On the Controllability of Delay-Differential Systems,. SIAM, J. Control,. vol. 5, No. 4, 1967, PP. 575-587.
Библиографическая ссылка
Василева М.В. О ТОЧЕЧНОЙ ПОЛНОТЕ СИСТЕМ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ ГИПЕРБОЛИЧЕСКОГО ТИПА // Современные проблемы науки и образования. – 2008. – № 3. ;URL: https://science-education.ru/ru/article/view?id=768 (дата обращения: 11.12.2023).