Фильтрация жидкости в упругодеформируемом анизотропном пласте представляет собой сложную многофазную систему, макроскопическое поведение которой под действием нагрузок в зависимости определяется протеканием многих параллельно идущих процессов различной механической природы. Задача определения напряженно-деформируемого состояние массива с учетом фильтрации в ней жидкости представляется достаточно сложной. Для ее постановки и решения требуются рациональная схематизация основных процессов, протекающих в пласте.
Аналогические задачи имеют практическую и, в частности экономическую важность при гидрогеологических и инженерно-геологических исследованиях. При этом возникает необходимость рассмотрения массива горных пород и фильтрующихся в нем жидкостей как единой механической системы, что приводит к комплексному подходу, базирующемся на методах, как механики деформируемого твердого тела, так и теории фильтрации.
Для описания фильтрационных течений в анизотропных пористых средах жидкости постулируется обобщенный закон Дарси. В общем случае линейная зависимость вектора скорости фильтрации и градиента фильтрационного давления приведен в работе [1].
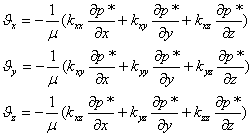(1)
где 
- компонент вектора скорости фильтрации,
- компоненты вектора градиента приведенного давления,
- компоненты симметричной матрицы, коэффициентов проницаемости.
Разновидности матрицы коэффициентов проницаемости определяет фильтрационные свойства пласта. Например,
1) 
- предназначен для изотропной пористой среды;
2) 
- задает фильтрационное свойства слоистых, т.е. трансверсально-изотропных сред;
3) 
- для ортотропных пористых сред;
4) 
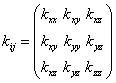- для анизотропные пористых, трещиноватых сред
Проницаемость пористой среды, называется величина, определяемая по формуле
, (2)
где 
- единичный вектор, задающий направление в пористой среде вдоль которого определяется направленная праницаемость;
- cкалярное произведение вектора скорости фильтрации и единичного вектора;
- модель градиента фильтрационного давления.
Подставляя (1) к формуле (2) имеем
.
Общий случай определения направления проницаемости имеет вид:
где 
- углы, которые образуют единичный вектор 
с координатными осями x,y,z.
В частности для трансверсально-изотропной среды направления проницаемости определяется как
.
Поэтому для трансверсально-изотропных сред фильтрационные свойст-ва задаются диагональными тензорами проницаемости с двумя разными коэффициентами соответственно.
В реальных коллекторах возможн-ость априорного определения главных направлений тензорами проницаемости является достаточно редкой.
В связи с изучением фильтра-ционных свойств пород в [2] рассмотрена типизация гидрогеологических условий. По результатам этих работ анизотропность горных пород оказывает существенное влияние на данные откачек и результаты расчета коэффициентов фильтрации пород.
Изучения геомеханических парамет-ров горных пород проводится лабора-торными и полевыми методами [3]. Поэтому коэффициенты фильтрации опре-деляются по данным фильтрационных ис-следований, в которых область возмуще-ний может достигать существенных раз-меров. В этом случая в результате расче-тов получаются значения параметров, усредненно характеризующие всю область опытного возмущение.
С позиции современной геологи-ческой науки поставленная задача явля-ется типичной задачей изучения и моде-лирования геологической неоднородности, неоднородности горных пород, вляющии на коэффициент фильтрации [4].
Аналогичным образом вектор фильтрации вводится в работе [5] при вы-воде уравнения фильтрации жидкости в анизотропной среде. Другой подход про-цедуры осреднения проиллюстрируем на изотропных средах с функции прони-цаемости вида
,
при наличии трещин, т.е. при x, y, z = const, которые моделируется бесконечно тонкими слоями, бесконечно большой для трещин и бесконечно малой для завес проницаемости [6]. Здесь 
- произвольные интегрируемые функции. Если в грунте с непроницаемыми блоками имеет место 
систем трещин, то из выведенных функций проницаемости следуют функции для эффективнойпроницаемости чисто трещиноватых сред.
Объемная деформация пористой среды равна изменению объема порового пространства, заполненной жидкостью. Поэтому в работе [7] выводится уравнение сплошности потока жидкости
, (3)
где n – пористость;
p – поровое давление жидкости;
K – модуль объемной сжимаемости жидкости;
- объемная деформация.
При этом напряжение массива горных пород имеет вид
,
здесь 
- эффективное напряжение, 
- символ Кронекера.
Из закона Гука для изотропной линейно-упругой пористой среды, связывающего эффективного напряжения и деформацию 
следует
. (4)
Уравнения (3), (4) определяет напряженно-деформируемое состояние скелета и нестационарное распределение порового давления.
Базовое уравнение связи напряжений и деформаций в твердой матрице с поровым давлением флюида для малых деформаций линейных и изотропных упругих сред при изотермических условиях было впервые выведено в [8]
,
где следующие коэффициенты Ляме выражается через коэффициент Пуассона 
и модуль Юнга 
, 
.
Тогда уравнение связи напряжений и деформаций имеет следующий вид [9]
,
где 
.
Используя закон Гука для пороупругой среды деформацию можно определить, как [10]
,
где 
- сумма главных напряжений, 
, 
.
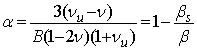Из недренированных пластов условий отношение между суммой главных напряжений и поровым давлением 
[11]
,
где 
-коэффициент Скемптона [12];
здесь 
-сжимаемость твердой фазы, скелета;
-сжимаемость порового флюида;
m-пористость;
получаем:
.
Дренированная сжимаемость скелета 
оценивается по формуле
.
Уравнение с учетом эффекта сжимаемости твердой и жидкой фазы, имеет вид [13]
.
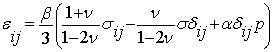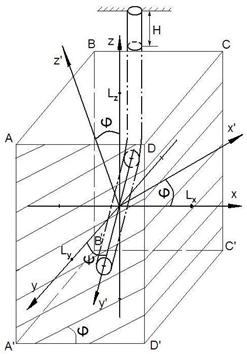
Рис. 1. Статическое состояние горизонтальной скважины, продольная ось которой составляет произвольный угол с линией простирания плоскости изотропии породного массива
Обобщение уравнений механики насыщенной упругой пористой среды [14-15] на случай среды с двойной пористости привен в работе [16]. Получен уравнения вектора перемещения пористой среды и давлений в блоках и трещинах.
В основу модели предложенный Ю.А.Буревичым [17] закладывается [18]: а) извесное в теории упругости формула для раскрытия эллипсоидальной полости под действием внутренного давления; б) кубическая зависимость расхода жидкости через плоскую щель от величины ее раскрытия; в) описание среднего тензора проницаемости ансамбля трещин через функцию распределения их по ориентацием.
Моделирование процесса фильтрации с учетом упругого деформирование пласта при отборе жидкости через горизонтальную скважину можно представить с помощью уравнений (1), где коэффициент фильтрации определяется из (2).
Пусть в расчетной области выполняется условия равновесия.
В данное время нерассмотрены вопросы изучение пространственнего фильтационного движение жидкости в изотропных, трансверсально-изотропных и анизотропных упругодеформируемых пористых средах со сложной геометрией. Появляется необходимость исследовании напряженно-деформируемого состояние как вертикальных или горизонтальных скважин, так и групп скважин, отбирающий жидкость в упругом трансверсально-изотропных пластах с наклонной плоскостью изотропии, т.е. в наклонных слоистых пористых средах.
Введем прямоугольную декартовую систему координат Оxyz таким образом, что ось Оz направлена вертикально вверх, горизонтальные оси Оx и Оy совпадают с линиями соответственно вкрест и вдоль простирания плоскости изотропии.
Упругое состояние трансверсально-изотропного массива описывается уравнением обобщенного закона Гука в системе координат Ox’y’z’, полученной путем поворота Оxyz на угол 
вокруг вертикальной оси Oz [19].
При этом полное напряжение [7] трансверсально-изотропного пласта может быть выражено через эффективного напряжения и давления, полученные при соответствующих решениях задачтеории фильтрации и упругости в виде
Характерной особенностью модели является предположение о том, что пористая матрица деформируется совершенно свободно до некоторого жесткого предела 
.
Таким образом фильтрация жидкости в деформируемой неоднородной (трансверсально-изотропной) пористой среде могут быть моделировании из совместных уравнений теории фильтрации и теории упругости.
СПИСОК ЛИТЕРАТУРЫ:
1. Басниев К.С., Дмитриев Н.М., Розенберг Г.Д. Нефтегазовая гидромеханика.– М.-Ижевск: Институт компьютерных исследований, 2005. – 544с.
2. Бабушкин В.Д., Плотников И.И., Чуйко В.М. Методы изучения фильтрационных свойств неоднородных пород. М.:Недра, 1974.-208с.
3. Шестаков В.М. Гидрогеомеханика. – М.: Изд-во МГУ. 1998. -72с.
4. Стасенко В.В., Климушин И.М., Бреев В.А. Методы изучение геологических неоднородности нефтяных пластов. М. :Недре, 1972. -134c.
5. Прусов И.А., Веремук И.А. Вывод оснавных уравнений фильтрации жидкости в анизотропной среде // Вести АН БелССР, №1, 1974. –с.109-112.
6. Холодовский С.Е. О фильтрации в пластах с кольцевыми неоднородными анизотропными зонами, трещинами и завесами // Докл. АН СССР. 1991, т.317. №3. с.606-608.
7. Фадеев А.Б. Метод конечных элементов в геомеханике. М.:Недра, 1987.-221с.
8. Biot M.A. General theory of three-dimensional consolidation // J. Appl. Phys. 1941. - V. 12. - P. 155-164.
9. Rice J.R., Cleary M.P. Some basic stress-diffusion solutions for fluid saturated elastic porous media with compressible constituents //Rev. Geophys. Space Phys. 1976. - V. 14. - P. 227-241.
10. Kumpel H.-J. Poroelasticity: parameters reviewed // Geophys. J. Int. 1991. - V. 105. - P. 783–799.
11. Skempton A.W. The pore-pressure coefficients A and B // Geotechnique. 1954.- V. 4. - P. 143-147.
12. Rojstaczer S., Agnew D.S. The influence of formation material properties on the response of water levels in wells to Earth tides and atmospheric loading. // J. Geophys. Res. 1989. - V. 94. - P. 12403-12411.
13. Копылова Г.Н., Болдина С.В. Оценка пороупругих параметров резервуаров подземных вод по данным уровнемерных наблюдений // Комплексные сейсмологические и геофизические исследования Камчатки. Петропавловск-Камчатский, 2004. С. 405 – 421.
14. Biot M.A. Mechanics of deformation and propagation in porous media. // Applied Phisics, 1962, v.33, v.4.-p.1482-1498.
15. Николаевский В.Н. Геомеханика и флюдодинамика. – М.:Недра, 1996. – 447с.
16. Wilson R.K., Aifantis E.C. On the theory of consolidation with double porosity// Int. Engng. Sci., 1982, v.20, №9. –p1009-1035.
17. Буевич Ю.А. Структурные-механические свойства и фильтрация в упругом трещинавато-пористом пласте // Инженерно-физический журнал, 1984, т.4. №4. –с.593-600.
18. Дияшев И.Р., Костерин А.В., Скворцов Э.В. Фильтрация жидкости в деформируемых нефтяных пластах.- Изд-во Казанского матем.общества, 1999.-238с.
19. Масанов Ж.К., Омаров А.Д., Махметова Н.М. Статическое и сейсмонапряженное состояние транспортных подземных сооружений в анизотропном геометрически нелинейном массиве. – Алматы: Бастау, 2002.-244с.
Библиографическая ссылка
Ажиханов Н.Т. НЕКОТОРЫЕ ВОПРОСЫ ИССЛЕДОВАНИЯ ФИЛЬТРАЦИИ ЖИДКОСТИ В АНИЗОТРОПНОЙ ПОРИСТОЙ СРЕДЕ // Современные проблемы науки и образования. 2008. № 3. ;URL: https://science-education.ru/ru/article/view?id=767 (дата обращения: 04.04.2025).