Для решения задач виброзащиты при проектировании и эксплуатации технологических машин и оборудования лесного комплекса существенным является построение математических моделей, отражающих зависимости параметров вибрации конструкций. В [4] рассматривается моделирование вибрации механической системы на примере массы фундамента, совершающей поступательные и поворотные перемещения в одной плоскости под воздействием установленного на ней однороторного машинного агрегата (рис. 1).
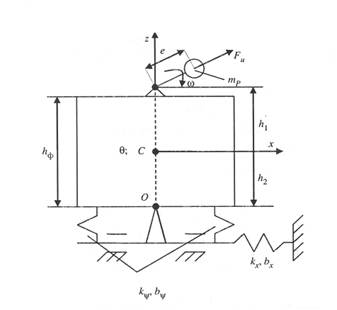
Рис. 1.
Система дифференциальных уравнений колебаний массы фундамента имеет вид:
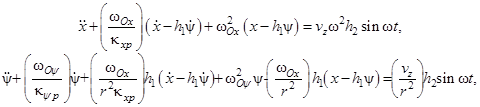(1)
здесь 
– частота вращения ротора, 
– горизонтальное перемещение центра массы, 
– поворотное перемещение массы, 
– расстояние по вертикали от центра масс установки до оси вращения ротора, 
– расстояние по вертикали от центра масс до центра тяжести опоры, 
– радиус инерции массы фундамента, 
– коэффициент, характеризующий меру уровня возбуждающих колебания сил инерции неуравновешенных масс ротора, 
– собственные частоты парциальных колебаний фундамента: горизонтальных и поворотных, 
– коэффициенты, соответствующие резонансу.
При разработке средств виброзащиты технологических машин одной из проблем математического моделирования является определение характера сил, воздействующих на фундамент при работе ротора, по измерениям наблюдаемых 
а также их скоростей 
Упомянутые силы зависят от характеристики грунтов, влажности и, в конечном счете, от времени. В связи с этим возникает задача определения сил неупругих сопротивлений, зависящих от 
и возникающих при взаимосвязи фундамента с грунтом. В цитируемой выше работе предполагалось, что указанные силы входят в систему линейно, что позволяло находить решение полученных уравнений в явном виде.
В работах [3; 5] А.В. Кряжимским и Ю.С. Осиповым был предложен метод динамической регуляризации, позволяющий в режиме реального времени моделировать приближение 
неизвестного воздействия 
в системе, описываемой обыкновенными дифференциальными уравнениями:
(2)
по результатам неточных измерений 
состояний системы: 
Здесь 
– евклидова норма, 
– узлы разбиения временного промежутка 
– вектор-функция и 
– матрица-функция, отображающие 
в 
и в пространство матриц размерности 
соответственно, – функция, обладающая минимальной нормой в L2[a,b] среди всех v(t), порождающих движение x(t). Считается известным, что 
– измеримая функция, со значениями из выпуклого компакта 
отображения 
и 
удовлетворяют условию Липшица по совокупности переменных.
Упрощенная схема упомянутого алгоритма, а также его модификация и получение соответствующего ей асимптотического порядка точности в случае постоянства подпространства собственных векторов матрицы 
рассматривались в [1]. Коротко остановимся на ее описании:
а) до начала работы алгоритма задаются положительные числа h, α=α(h), Δ=Δ(h), 
б) выбираются узлы ti (
ti+1 - ti = ∆) разбиения промежутка 
;
в) на каждом шаге алгоритма (на временном промежутке [ti, ti+1)) выполняются следующие действия:
1) в момент ti проводят измерение xh(ti) состояния системы x(ti) так, что |xh(ti) - x(ti) | ≤ h;
2) определяется состояние в моменты ti системы – модели с начальным условием w(t0)=xh(t0), функционирующей на [ti, ti+1) по правилу
где vi – проекция на Q вектора
Таким образом, результатом работы алгоритма является построение приближения воздействия в виде кусочно-постоянной функции v(t)=vi при 
Если вычисление vi требует выполнения конечного числа арифметических операций, то при достаточном быстродействии вычислительного устройства формирование приближения v(t) может быть осуществлено в темпе реального времени. Поэтому рассматриваемый метод получил название конечношагового динамического алгоритма (к.д.а).
В работе [1] было показано, что при выборе Δ=h, 
и достаточно большом значении 
найдется положительная константа C такая, что 
(
– норма в пространстве L1[a,b]).
Для практических целей зачастую более удобной является возможность получения оценки на неограниченном временном промежутке в равномерной метрике. Такая возможность для рассматриваемого метода была доказана в работе [2].
Отметим, что замена 
, 
приводит (1) к системе вида
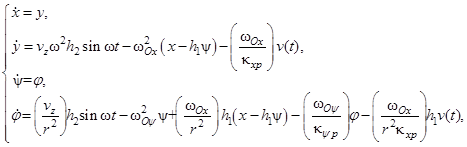(3)
которая, очевидно, является частным случаем (2). Метод динамической регуляризации, примененный к (3), позволяет по измерениям 
и 
восстановить характер неупругой силы – . Ниже для модельного примера на рисунке 2(а) продемонстрирована зависимость восстановленного с помощью описанного выше метода воздействия 
от времени 
, на рисунке 2(б) – зависимость от 
:
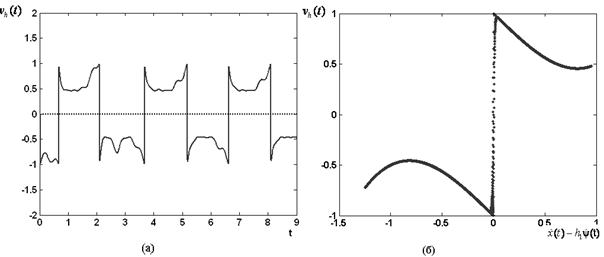
Рис. 2.
Результаты моделирования процесса показывают, что воздействующие силы носят существенно нелинейный характер в отличие от того, как это предполагалось первоначально. Таким образом, метод динамической регуляризации позволяет уточнять рассматриваемые математические модели, что позволяет более адекватно описывать изучаемые процессы.
Рецензенты:
Старжинский В.Н., д.т.н., профессор, заведующий кафедрой ФГБОУ ВПО «Уральский государственный университет», г. Екатеринбург.
Часовских В.П., д.т.н., профессор, декан факультета экономики и управления ФГБОУ ВПО «Уральский государственный университет», г. Екатеринбург.
Библиографическая ссылка
Вдовин А.Ю., Куцубина Н.В., Рублева С.С., Санников А.А. К ВОПРОСУ ОБ УТОЧНЕНИИ МАТЕМАТИЧЕСКОЙ МОДЕЛИ МЕХАНИЧЕСКОЙ СИСТЕМЫ МЕТОДОМ ДИНАМИЧЕСКОЙ РЕГУЛЯРИЗАЦИИ // Современные проблемы науки и образования. 2013. № 1. ;URL: https://science-education.ru/ru/article/view?id=7652 (дата обращения: 11.05.2025).