Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы

Королев Л.В., Таршис М.Ю.

В работе предлагается математическая модель процесса смешивания сыпучих фракций, сильно различающихся по размеру частиц, в открытом ленточном устройстве барабанного типа с прямой подачей мелкой фракции в установившийся поток обрушения на свободной поверхности крупной фракции. Определен оптимальный режим дозирования и распределения мелкой фракции вдоль поверхности обрушения. Полученные значения коэффициента неоднородности смеси на разных этапах процесса согласуются с экспериментальными данными.

Статья в формате PDF

186 KB

Технологии создания высокоплотных сыпучих смесей имеют большое значение для производства различных композиционных материалов, например, асфальто- и цементобетонов, обладающих высокими прочностными характеристиками при сравнительно низком расходе дорогостоящего связующего. В соответствии с результатами теоретических исследований [6] и рекомендациями нормативных документов [3], высокоплотные смеси должны иметь прерывистые зерновые составы, в которых присутствуют фракции, не менее чем на порядок различающиеся по размеру, а промежуточные фракции исключены. Такие смеси, как известно, имеют сильную склонность к сегрегации [1, 7], что существенно усложняет процесс их приготовления. Одним из возможных способов получения этих смесей является гравитационно-пересыпное смешивание в открытом ленточном устройстве барабанного типа [8] с прямой подачей мелкой фракции на свободную поверхность установившегося потока обрушения крупной фракции [9]. Такой способ смешивания позволяет за счет выбора оптимального режима дозирования мелкой фракции получить смесь необходимого качества до появления эффектов сегрегации [5]. В настоящей работе предлагается математическая модель этого процесса.

Рассмотрим работу ленточного смесителя, изображенного на Рис. 1 [8]. Если загрузка компонентов смеси в рабочий объем происходит до начала движения ленты, то процесс смешивания в рассматриваемом устройстве принципиально не отличается от процесса смешивания в гладком цилиндрическом барабане [2, 5, 7]. При движении гибкой ленты, огибающей валы и прижимные диски, ограничивающие рабочий объем, сыпучий материал поднимается вверх с постоянной угловой скоростью  по цилиндрической поверхности ленты радиуса . По достижении свободной поверхностью сыпучего материала некоторого угла наклона к горизонту (угла обрушения), частицы ссыпаются по этой поверхности вниз. Таким образом, при работе смесителя образуются две зоны движения сыпучего материала: транспортирующая зона, в которой частицы двигаются синхронно с лентой по линиям тока постоянного радиуса (на Рис. 1 показана линия тока ), и приповерхностный поток обрушения , в котором имеет место хаотическое движение частиц и происходит их перераспределение по линиям тока. При равенстве насыпных плотностей смешиваемых фракций характер этого перераспределения определяется отношением размеров частиц. Если частицы смешиваемых компонентов одинаковы по размеру, то в нижней части зоны обрушения они с одинаковой вероятностью попадают в любую линию тока, в результате чего за время порядка нескольких  происходит полное перемешивание первоначально разделенных фракций. Если же имеет место существенное различие смешиваемых фракций по размеру, то мелкие частицы, способные проникать в промежутки между крупными, имеют значительно большую вероятность попадания в ближайшую линию тока, в результате чего они группируются в центральной части занятого сыпучей массой сегмента (в окрестности точки О на Рис. 1), а крупные – на периферии. Как показывают эксперименты [5], если диаметры частиц различаются на порядок, то практически полная сегрегация однородной смеси происходит за время, не превышающее . Такая интенсивная сегрегация снижает эффективность использования обычных барабанных смесителей для приготовления высокоплотных смесей [1, 7].

Смеситель с открытым рабочим объемом позволяет применить другой, более эффективный в случае сильно сегрегирующих фракций режим смешивания [9]. Перед пуском смесителя в него загружается только крупная фракция, объем которой близок к объему всей смеси. За время порядка  после начала движения ленты на поверхности сыпучего материала устанавливается поток обрушения. В нижний участок установившегося потока через дозатор Д (Рис. 1) начинают подаваться частицы мелкой фракции, которые, заполняя промежутки между крупными частицами, попадают на линии тока, ближайшие к точке падения. Дозирование при этом осуществляется с таким расчетом, чтобы нормальная к поверхности составляющая плотности потока падающих частиц в окрестности любой точки поверхности  была пропорциональна длине линии тока , исходящей из этой точки. Время дозирования должно быть близким к , но не превышать его, так как процесс должен завершиться до начала сегрегации при вторичном попадании частиц в поток обрушения. В момент окончания подачи мелкой фракции лента останавливается, а готовая смесь выгружается из рабочего объема, например, с помощью реверса ленты.

Рассмотрим математическую модель описанного процесса смешивания [2, 4, 5]. Будем характеризовать состояние смеси функцией , определяющей объемную долю мелкой фракции в каждой точке  поперечного сечения рабочего объема в момент времени . Направим ось  вдоль линии обрушения, выбрав начало отсчета О в середине хорды, ограничивающей занятый материалом сегмент (Рис. 1). Длину хорды, определяемую объемом загрузки, положим равной . В нулевом приближении по толщине слоя обрушения функция , вообще говоря, терпит разрыв вдоль линии обрушения. Поэтому целесообразно рассматривать отдельно функцию , определяющую долю мелкой фракции в поверхностном потоке, и , определяющую долю мелкой фракции в транспортирующей зоне. Эволюция распределения  задается обычным транспортным уравнением

                                            (1)

где  - поле скоростей движения частиц в транспортирующей зоне, а  - оператор градиента. В свою очередь, функция  должна определяться исходя из условия сохранения объема мелкой фракции при переходе частиц из транспортирующей зоны в поток обрушения и обратно с учетом падающего потока:

                                (2)

где  –плотность полного поверхностного потока сыпучего материала,  - нормальная к поверхности составляющая плотности потока падающих частиц, а  – нормальная к линии обрушения составляющая скорости в транспортирующей зоне.

Поверхностный поток  можно легко определить, если принять во внимание, что в рассматриваемом процессе при добавлении мелкой фракции общий объем смеси практически не изменяется, поскольку фракционный состав для высокоплотных смесей подбирается таким образом [3, 6], чтобы мелкие частицы заполняли пустоты между крупными частицами, не раздвигая их. В этом предположении объемные концентрации крупных частиц в транспортирующей зоне  и в потоке обрушения  также связаны между собой уравнением (2) с тем различием, что последнее слагаемое  должно браться с отрицательным знаком, что отвечает уменьшению объема пустот, который входит в объемную долю крупной фракции. Складывая это уравнение с уравнением (2) и учитывая, что , получаем для плотности полного поверхностного потока уравнение , которое с граничным условием  дает [2]:

                                                 (3)

Уравнение (1) позволяет вычислить долю мелкой фракции в любой точке рабочего объема , в том числе и на поверхности при , если задано начальное распределение  и известны значения  при  и . Функцию  можно найти, решая дифференциальное уравнение (2) для  с учетом (3) при , если известны граничное условие , связь между  и , а также задана плотность падающего потока .

Граничное условие для  при  можно найти, интегрируя обе части уравнения (2) по  в пределах от  до . Предполагая, что внешний поток при  отсутствует, получаем [2]:

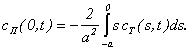                                               (4)

Для установления связи между функциями  и  рассмотрим микрообъем сыпучего материала  в окрестности точки  на линии обрушения. Пусть  - вероятность перехода одной частицы мелкой фракции из потока обрушения в транспортирующую зону в данной точке, а  - та же вероятность для частицы крупной фракции. Тогда в транспортирующей зоне в окрестности точки  объем мелкой фракции составит , объем крупной - , а объемная доля мелкой фракции в транспортирующей зоне будет равна [4]:

                   (5)

где  – отношение вероятностей попадания на линию тока в окрестности точки  частиц мелкой и крупной фракций, которое определяет характер распределения частиц по линиям тока при входе в транспортирующую зону. Как показывает анализ численных и натурных экспериментов, удовлетворительное количественное описание процесса смешивания в рамках предлагаемой модели достигается, если принять вероятность перехода частицы из потока обрушения в транспортирующую зону равной , где  - размер частицы,  - средний размер частиц в данной области потока обрушения,  - числовой коэффициент. Тогда функция  запишется в виде:

                               (6)

где  - отношение диаметров частиц мелкой и крупной фракции.

Плотность потока мелкой фракции, подаваемой из дозатора,  должна рассчитываться исходя из требования наиболее равномерного распределения мелких частиц по объему смеси во время подачи и предотвращения вторичного попадания мелких частиц в поток обрушения, приводящего к сегрегации смеси. Наиболее просто величина  вычисляется, если объем загрузки сыпучего материала, отнесенный к ширине ленты, близок к , и, соответственно, . В этом случае все линии тока имеют одинаковый угловой размер , что позволяет для всех значений  установить одинаковое время начала подачи  и продолжительность подачи . Зависимость плотности потока от  можно установить, приняв во внимание, что в течение времени подачи поток обрушения при  не содержит мелкой фракции, и, согласно (4), , а в нижней части зоны обрушения падающие из дозатора мелкие частицы незначительно увлекаются потоком крупной фракции, попадая в транспортирующую зону недалеко от места падения. В этом предположении левую часть уравнения (2) можно считать равной нулю, а  в правой части положить равной требуемой объемной доле мелкой фракции в смеси . Тогда из (2), с учетом найденного времени начала и продолжительности подачи, следует:

                    (7)

где  при  и  при . Если объем загрузки меньше  и , то выражение для  сохраняет свой вид, если положить , , где  - угловой размер линии тока. Зависимость времени начала подачи от  выбирается с таким расчетом, чтобы частицы мелкой фракции, двигающиеся по любой линии тока, одновременно достигли линии обрушения в момент прекращения подачи через дозатор, что обеспечивает равномерное распределение мелких частиц по объему смеси.

Таким образом, предлагаемая математическая модель позволяет описать процесс приготовления смеси сыпучих фракций, сильно различающихся по размеру частиц, в ленточном устройстве гравитационно-пересыпного действия с дозируемой подачей мелкой фракции в поток обрушения (Рис. 1). Объемная доля мелкой фракции в любой точке рабочего объема  находится путем решения дифференциального уравнения в частных производных (1) с начальным условием , определяемым первоначальной загрузкой материала в смеситель, и с граничным условием на нижней части линии обрушения  при . Функция , в свою очередь, находится в каждый момент времени  путем решения обыкновенного дифференциального уравнения (2) с граничным условием (4) с учетом соотношений (3), (5), (6). При этом нормальная к поверхности обрушения составляющая плотности падающего из дозатора потока  задается выражением (7). По известному распределению мелкой фракции  можно на любой стадии смешивания определить коэффициент неоднородности , который характеризует качество получаемой смеси [1, 7]:

                                      (8)

где  обозначает усреднение по объему смеси.

На Рис. 2 представлены результаты вычисления коэффициента неоднородности  (8) по предлагаемой модели, сопоставленные с экспериментальными данными для установки Рис. 1 [8] с погонной загрузкой песчаной смеси , долей мелкой фракции , размерами частиц крупной и мелкой фракции соответственно  и . Оптимальное качество смеси достигается в момент окончания подачи мелкой фракции . При дальнейшем движении ленты начинается процесс сегрегации смеси и ее качество ухудшается. Удовлетворительное согласие расчетных и экспериментальных данных позволяет сделать вывод о правомерности использования предложенной модели процесса смешивания.

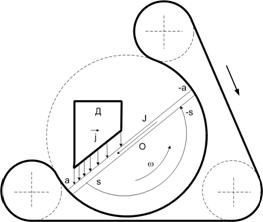
Рис. 1. Схема смесительного устройства [8]

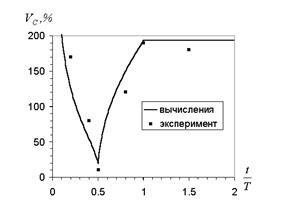
Рис. 2. Изменение коэффициента неоднородности в процессе смешивания с прямой подачей в поток обрушения

СПИСОК ЛИТЕРАТУРЫ:

1.  Fan L.T., Yi-Ming C., Lai F.S. // Powder Technology, 1990, v. 61, p. 255-287.

2.  Prigozhin L., Kalman H. // Phys.Rev. E. 1998. v 57 (2) p. 2074-2080.

3.  ГОСТ 9128-97. Смеси асфальтобетонные дорожные, аэродромные и асфальтобетон. Технические условия. – М., Госстандарт, 1999 – 16 с.

4.  Зайцев И.А., Королев Л.В., Таршис М.Ю. // Транспортная модель процесса смешивания сыпучих материалов, Международная научная конференция «Основы создания новых высокоэффективных химико-технологических процессов и оборудования», Сборник трудов, Иваново, 2001, с. 251-253

5.  Королев Л.В., Таршис М.Ю. // Изв. ВУЗов. Химия и химическая технология. 2002. т. 45, вып. 7, с91-93.

6.  Королев Л.В. и др. // Современные проблемы науки и образования, 2007. №6, с. 105-108.

7.  Макаров Ю.И. Аппараты для смешения сыпучих материалов М.: Машиностроение, 1973, 216 с.

8.  Патент RU 2191622 C1 7 B 01 F 3/18. Смеситель // Таршис М. Ю. и др. (Ярославский государственный технический университет).

9.  Патент RU 2254907 C1 B 01 F 3/18. Способ приготовления смеси сыпучих материалов // Таршис М.Ю. и др. (Ярославский государственный технический университет).

Библиографическая ссылка