Диагностика играет в медицине важнейшую роль, и постановка диагноза требует от врача большого мастерства, знаний и интуиции. Точность диагноза и быстрота, с которой его можно поставить, зависят, разумеется, от очень многих факторов: от состояния больного, от имеющихся данных о симптомах и признаках заболевания и результатах лабораторных анализов, от общего объема медицинской информации о наблюдении таких симптомов при самых различных заболеваниях и, наконец, от квалификации самого врача. Своевременно поставленный точный диагноз часто облегчает выбор метода лечения и значительно повышает вероятность выздоровления больного. Исходя из всех этих соображений, вполне естественно попытаться определить условия, при которых диагноз может быть поставлен максимально быстро и точно. В течение многих веков врачи с переменным успехом предпринимали попытки решить эту задачу. Однако в последние годы благодаря применению современных методов лечения и диагностики, основанных на новейших достижениях науки и техники, возможности получения успешных результатов значительно возросли. Поэтому важно найти точные методы описания, исследования, оценки и контроля процесса постановки диагноза. Нейронные сети – мощный метод для решения задач распознавания образов в ситуациях, когда в экспериментальных данных отсутствуют значительные фрагменты информации, а имеющаяся информация предельно зашумлена [3].
Также в медицинской диагностике распространен дискриминантный анализ. При его использовании главным показателем является точность классификации.
Нейронные сети представляют собой нелинейные системы, позволяющие гораздо лучше классифицировать данные, чем обычно используемые линейные методы. В приложении к медицинской диагностике они дают возможность значительно повысить специфичность метода, не снижая его чувствительности.
В отличие от традиционных средств обработки информации, программирование нейронных сетей осуществляется неявно в процессе обучения. Обучение строится следующим образом: существует так называемый задачник, то есть набор примеров с заданными ответами. Эти примеры предъявляются системе. Нейроны получают условия примеров и преобразуют их. Далее нейроны несколько раз обмениваются преобразованными сигналами и, наконец, выдают ответ в виде набора сигналов. Отклонение от правильного ответа штрафуется. Обучение заключается в минимизации штрафа как неявной функции связей.
Важнейшее свойство нейронных сетей, свидетельствующее об их огромном потенциале и широких прикладных возможностях, состоит в параллельной обработке информации одновременно всеми нейронами. Благодаря этой способности при большом количестве межнейронных связей достигается значительное ускорение процесса обработки информации. Очень большое количество межнейронных соединений приводит к тому, что сеть становится нечувствительной к ошибкам, возникающим в отдельных контактах. Функции поврежденных соединений принимают на себя другие элементы, в результате в деятельности сети не наблюдаются заметные нарушения [5]. Другое не менее важное свойство нейронной сети состоит в способности к обучению и к обобщению полученных знаний [1].
Дискриминантный анализ – это раздел математической статистики, содержанием которого является разработка методов решения задач различения (дискриминации) объектов наблюдения по определенным признакам. При использовании метода дискриминантного анализа главным показателем является точность классификации, и этот показатель можно легко определить, оценив долю правильно классифицированных при помощи прогностического уравнения наблюдений. Если исследователь работает с достаточно большой выборкой, применяется следующий подход: выполняется анализ по части данных, а затем прогностическое уравнение применяется для классификации наблюдений во второй половине данных. Точность прогноза оценивается, т.е. происходит перекрестная верификация. В дискриминантном анализе существуют методы пошагового отбора переменных, помогающие осуществить выбор предсказывающих переменных [2].
Рассмотрим возможности использования нейросетевых технологий и дискриминантного анализа в задачах медицинской диагностики на примере задачи дифференциальной диагностики бронхиальной астмы.
Имеется выборка X из m объектов (пациентов с различными формами бронхиальной астмы), характеризующихся n переменными (показатели бронхолегочной системы)
X=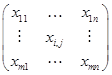 ,(1)
,(1)
где i – номер объекта (пациента); j – номер переменной (признака).
Вектор Y={y1,…,yi,…,yk}, где yi – один из возможных диагнозов (различные формы бронхиальной астмы); k – количество диагностируемых классов (возможных диагнозов).
Таким образом, задача заключается в построении модели дифференциальной диагностики бронхиальной астмы, т.е. построение решающего правила для отнесения i-го объекта (i=1…m) (пациента) с определенным набором признаков j (j=1...n) к одному из имеющихся классов yi (i=1...k) (диагнозов), т.е. решение задачи классификации.
Задача классификации представляет собой задачу отнесения образца к одному из нескольких попарно не пересекающихся множеств. При решении задач классификации необходимо отнести имеющиеся статические образцы (характеристики ситуации на рынке, данные медосмотра, информация о клиенте) к определенным классам. Возможно несколько способов представления данных. Наиболее распространенным является способ, при котором образец представляется вектором. Компоненты этого вектора представляют собой различные характеристики образца, которые влияют на принятие решения о том, к какому классу можно отнести данный образец. В нашем случае в качестве компонентов этого вектора будут данные из медицинской карты больного. Таким образом, на основании некоторой информации о примере необходимо определить, к какому классу его можно отнести. Классификатор, таким образом, относит объект к одному из классов в соответствии с определенным разбиением N-мерного пространства, которое называется пространством входов, и размерность этого пространства является количеством компонент вектора.
Персептрон представляет собой сеть, состоящую из нескольких последовательно соединенных слоев формальных нейронов МакКаллока и Питтса. На низшем уровне иерархии находится входной слой, состоящий из сенсорных элементов, задачей которого является только прием и распространение по сети входной информации. Далее имеются один скрытый слой. Каждый нейрон на скрытом слое имеет несколько входов, соединенных с выходами нейронов предыдущего слоя или непосредственно со входными сенсорами X1...Xn, и один выход. Нейрон характеризуется уникальным вектором весовых коэффициентов W. Веса всех нейронов слоя формируют матрицу, которую мы будем обозначать V. Функция нейрона состоит в вычислении взвешенной суммы его входов с дальнейшим нелинейным преобразованием ее в выходной сигнал: ![]()
(2)
Выходы нейронов последнего, выходного, слоя описывают результат классификации Y=Y(X). Матрицу весовых коэффициентов от входов к скрытому слою обозначим W, а матрицу весов, соединяющих скрытый и выходной слой – как V. Для индексов примем следующие обозначения: входы будем нумеровать только индексом i, элементы скрытого слоя – индексом j, а выходы, соответственно, индексом k.
Пусть сеть обучается на выборке (Xa,Ya), α=1…p. Активности нейронов будем обозначать малыми буквами y с соответствующим индексом, а суммарные взвешенные входы нейронов – малыми буквами x. Начальные значения весов всех нейронов всех слоев V(t=0) и W(t=0) полагаются случайными числами. Сети предъявляется входной образ Xa, в результате формируется выходной образ Ya. При этом нейроны последовательно от слоя к слою функционируют по следующим формулам:
скрытый слой:
![]()
![]()
выходной слой:
![]()
![]()
Здесь f(x) – сигмоидальная функция, определяемая по формуле (2).
Функционал квадратичной ошибки сети для данного входного образа имеет вид:
![]()
Таким образом, необходимо найти матрицу весов V, которая даст минимальную ошибку обучения нейронной сети.
Альтернативными способами решения задач классификации являются методы дискриминантного анализа, в котором реализованы методы классической статистики. В теории анализа многомерных данных всесторонне разработаны процедуры построения линейных дискриминантных функций (ЛДФ), обеспечивающих при определенных предположениях минимум критерия средней вероятности ошибочной классификации. Так, для случая двух классов ![]() и
и ![]() методы построения ЛДФ опираются на два предположения [4].
методы построения ЛДФ опираются на два предположения [4].
Первое состоит в том, что области ![]() и
и ![]() , в которых концентрируются объекты из двух классов, могут быть разделены (p-1)-мерной гиперплоскостью:
, в которых концентрируются объекты из двух классов, могут быть разделены (p-1)-мерной гиперплоскостью:
![]()
Коэффициенты ![]() в данном случае интерпретируются как параметры, характеризующие наклон гиперплоскости к координатным осям, а
в данном случае интерпретируются как параметры, характеризующие наклон гиперплоскости к координатным осям, а ![]() называются порогом и соответствует расстоянию от гиперплоскости до начала координат. Второе предположение касается критерия качества разделения областей
называются порогом и соответствует расстоянию от гиперплоскости до начала координат. Второе предположение касается критерия качества разделения областей ![]() и
и ![]() гиперплоскостью
гиперплоскостью ![]() . Вектор оптимальных весовых коэффициентов w определяется следующим образом:
. Вектор оптимальных весовых коэффициентов w определяется следующим образом:
![]() ,
,
где ![]() – вектор средних значений признаков для класса
– вектор средних значений признаков для класса ![]() .
.
Если объекты каждого класса имеют многомерное нормальное распределение с одинаковой ковариационной матрицей S и векторами средних значений ![]() , то пороговое значение
, то пороговое значение ![]() , минимизирующее критерий средней вероятности ошибки, будет:
, минимизирующее критерий средней вероятности ошибки, будет:![]() .
.
В качестве исходной информации использовались данные клиники, в которой зарегистрированы результаты исследования 83 человек с установленным диагнозом бронхиальной астмы. 23 человека – первая группа – бронхиальная астма психогенно-индуцированная; 19 человек – вторая группа – бронхиальная астма сомато-психогенная; 29 человек – третья группа – бронхиальная астма непсихогенная, 12 человек – четвертая группа – психогенная одышка (не болеют бронхиальной астмой). Для каждого человека имеются результаты анализов: физиологические показания дыхания (минутный объем дыхания, жизненная емкость легких, форсированная емкость легких, объем форсированного выдоха за 1 с и т.д.), психологические показания (депрессия по Беку, депрессия по Цунгу, тревога реактивная, тревожность личностная, тревога по Шихану, степень вентиляционной недостаточности и т.д.), индексированные значения физиологических показаний – динамика показателей функции легких. В общем 173 различных показания, по которым можно наиболее точно определить болеет ли человек бронхиальной астмой, и если да, то ее тип.
Нейрон представляет собой единицу обработки информации в нейронной сети. На рис. 1 приведена модель нейрона, лежащая в основе искусственных нейронных сетей.
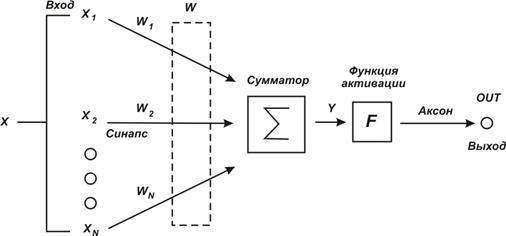
Рис. 1. Модель искусственного нейрона.
В этой модели нейрона можно выделить три основных элемента:
- синапсы, каждый из которых характеризуется своим весом или силой. Осуществляют связь между нейронами, умножают входной сигнал ![]() на весовой коэффициент синапса
на весовой коэффициент синапса ![]() , характеризующий силу синаптической связи;
, характеризующий силу синаптической связи;
- сумматор, аналог тела клетки нейрона. Выполняет сложение внешних входных сигналов или сигналов, поступающих по синаптическим связям от других нейронов. Определяет уровень возбуждения нейрона;
- функцию активации, определяющую окончательный выходной уровень нейрона, с которым сигнал возбуждения (торможения) поступает на синапсы следующих нейронов.
Модель нейрона имитирует в первом приближении свойства биологического нейрона. На вход искусственного нейрона поступает некоторое множество сигналов, каждый из которых является выходом другого нейрона. Каждый вход умножается на соответствующий вес, пропорциональный синаптической силе, и все произведения суммируются, определяя уровень активации нейрона.
Для построения модели дифференциальной диагностики бронхиальной астмы будем использовать многослойный персептрон.
На практике чаще всего используют двухслойный персептрон. Рассмотрим схему двухслойного персептрона, представленную на рисунке 2.
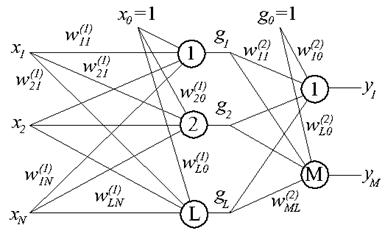
Рис. 2. Структурная схема двухслойного персептрона.
Здесь gl, l=1, 2, ..., L – выходные сигналы первого слоя нейронов. Верхние индексы в скобках (m), m=1, 2, означают номер слоя нейрона.
Для исключения коллизий следует отметить, что понятие «слой» часто применяют по отношению к сигналам ИНС (а не к нейронам). В таком смысле представленная на рисунке сеть – трехслойная: входные сигналы сети x1,x2,… xN составляют входной слой, выходные сигналы первого нейронного слоя g1,g2,… gL образуют первый скрытый слой, а выходные сигналы y1,y2,… yM – слой выходной. Для обозначения структуры сети используется кодировка в виде «N-L-M».
Выходные сигналы нейронных слоев легко рассчитываются по следующим формулам:
![]()
![]()
Необходимо подчеркнуть, что функции активации абсолютно всех нейронов сети абсолютно идентичны. Цель обучения многослойного нейрона заключается в подборе таких значений всех весовых коэффициентов сети w(1)li и w(2)li, которые обеспечивают максимальное совпадение выходного вектора Yk и эталонного вектора ожидаемых значений Dk при предъявлении входного вектора Xk.
В случае единичной обучающей выборки целевая функция задается в виде:
![]()
![]()
В случае нескольких обучающих пар целевая функция превращается в сумму по всем парам:
![]()
Для компьютерной реализации диагностической модели с помощью многослойного персептрона была выбрана система Matlab, для реализации модели с помощью дискриминантных функций выбрали систему StatGraphics. В результате была построена модель дифференциальной диагностики бронхиальной астмы, которая с определенной точностью может отнести индивида к определенной группе из представленных четырех.
После исследования модели в двух разных программах получили следующие результаты.
1. Модель, построенная с помощью многослойного персептрона, не во всех случаях является надежной. Обучив и протестировав полученную модель, можно сделать вывод, что для построения нейросети нужно больше примеров – показателей больных бронхиальной астмой. При физиологических показаниях мы получили неудовлетворительные результаты. Такая модель является ненадежной. При моделировании с психологическими показаниями и индексами физиологических и психологических показаний мы получили хорошие результаты – совпадение свыше 80%, что говорит о надежности полученной модели.
2. Модель, построенная с помощью дискриминантного анализа, дала наилучшие результаты в случае использования физиологических показателей больных – точность диагностики больных первой группы составляет 95,65%, второй группы – 94,74% и третьей группы 93,10%. Это довольно точные результаты, которые могут в какой-то мере содействовать окончательному заключению специалиста. Вместе с тем констатация отсутствия бронхиальной астмы (группа 4) осуществляется со 100%-ной надежностью. При использовании психологических показателей качество распознавания построенной модели не превышало 50%. При индексах физиологических и психологических показателей мы получили следующие результаты: качество распознавания на контрольной выборке составило 82%, что является достаточно хорошим результатом для задач медицинской диагностики.
Полученная диагностическая модель будет использована в системе поддержки принятия решения диагностики и лечения бронхолегочных заболеваний.
Выводы
В медицине важно найти точные методы описания, исследования, оценки и контроля процесса постановки диагноза. Наилучший путь к точности и логике рассуждений при решении любой задачи – это математический подход. В принципе этот подход можно выбирать независимо от того, насколько труден и сложен рассматриваемый вопрос. Если мы имеем дело с большим числом взаимозависимых факторов, обнаруживающих значительную естественную изменчивость, то для достаточно эффективного описания сложной схемы их влияния существует лишь один способ – использование соответствующего статистического метода. Если число факторов или число категорий данных очень велико, то желательно, или даже необходимо, использовать компьютер, чтобы искомые результаты можно было получить за достаточно короткое время. Такой подход ни в коей мере не умаляет диагностических способностей врача. Напротив, он открывает еще больший простор для проявления этих качеств, освобождая врача от необходимости заниматься такими проблемами, которые можно сформулировать в численной и логической форме и, следовательно, решать математическими методами и с помощью вычислительной техники.
Имеющиеся в настоящее время данные свидетельствуют о том, что вычислительные машины, несомненно, могут играть важную роль при постановке диагноза; оценке точности диагнозов, которые ставят врачи, с целью повышения общего уровня диагностики; создании учебных пособий для студентов, а также для сбора, обобщения и обработки клинических данных для квалифицированного использования их врачами при постановке диагноза.
Работа выполнена при финансовой поддержке РГНФ, проект 12-06-12057 «Создание системы алгоритмических и программных средств обработки, представления и анализа экспериментальных данных в социальных и медицинских исследованиях».
Рецензенты:
Иванкина Любовь Ивановна, д.ф.н., профессор, Национальный исследовательский Томский политехнический университет, г. Томск.
Коваль Тамара Васильевна, д.ф.-м.н., профессор, Национальный исследовательский Томский политехнический университет, г. Томск.
Библиографическая ссылка
Семерякова Е.Г., Берестнева О.Г., Макарова Л.С. МАТЕМАТИЧЕСКИЕ МЕТОДЫ В ЗАДАЧАХ МЕДИЦИНСКОЙ ДИАГНОСТИКИ // Современные проблемы науки и образования. 2012. № 6. ;URL: https://science-education.ru/ru/article/view?id=7472 (дата обращения: 29.01.2026).



