Введение
Для численного решения жестких систем обыкновенных дифференциальных уравнений обычно применяются L-устойчивые методы [6]. При реализации таких численных схем на каждом шаге несколько раз решается линейная система алгебраических уравнений с применением LU-разложения матрицы Якоби. Решение осуществляется с выбором главного элемента по строке или столбцу, а иногда и по всей матрице. При большой размерности исходной задачи общие вычислительные затраты фактически полностью определяются временем декомпозиции данной матрицы. Сокращения вычислительных затрат достигают за счет применения одной матрицы на нескольких шагах [3; 4; 6]. Наиболее естественно это осуществляется в итерационных методах, где данная матрица только определяет скорость сходимости итерационного процесса [6]. Для безытерационных методов типа Розенброка [7] и их модификаций [5; 6] вопрос о замораживании матрицы Якоби более сложный. В таких методах эта матрица включена в численную схему, и поэтому ее аппроксимация приводит к потере порядка точности численной формулы. Максимальный порядок методов типа Розенброка с замораживанием матрицы Якоби равен двум [3]. Безытерационные методы просты с точки зрения реализации и, как следствие, привлекательны для вычислителей. В [5] предложен новый класс одношаговых численных схем, которые были названы (m,k)-методами. Они столь же просты при реализации, как и методы типа Розенброка, но обладают более хорошими свойствами точности и устойчивости. Более существенно, они достаточно просто реализуются с замораживанием матрицы Якоби.
Здесь разработан L-устойчивый (3,2)-метод третьего порядка для решения жестких задач. На основе оценки глобальной ошибки построено неравенство для контроля точности вычислений. Оценка осуществляется через ранее вычисленные стадии. Сформулирован параллельный алгоритм для вычислительных систем кластерной архитектуры.
1. Класс (m, k) -методов решения жестких задач
Рассмотрим задачу Коши для системы дифференциальных уравнений вида
, 
, 
,(1)
где y и f − вещественные N-мерные вектор-функции, t − независимая переменная. Пусть Z − множество целых чисел, и заданы числа m, kÎZ, k≤m. Обозначим через Mm множество чисел {iÎZ, 1≤i≤m}, а через Mk и Ji, 1<i≤m, подмножества из Mm вида
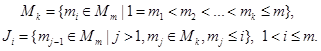
Тогда класс (m,k)-методов записывается следующим образом:
, 
,
, 
, (2)
, 
,
где ki, 1≤i≤m, − стадии метода, a, pi, βij, αij и cij − постоянные коэффициенты, h − шаг интегрирования, E − единичная матрица, f′n=∂f(yn)/∂y − матрица Якоби системы (1), k − количество вычислений функции f на шаге, m − число стадий. На каждом шаге интегрирования осуществляются одно вычисление матрицы Якоби и одна декомпозиция матрицы Dn. Так как k и m полностью определяют затраты на шаг, а набор чисел m1,…, mk из множества Mk только распределяет их внутри шага, то методы типа (2) названы (m,k)-методами. При k=m и αij=cij=0 схемы (2) совпадают с методами типа Розенброка [7].
2. Исследование (3, 2)-метода
Рассмотрим численную формулу вида
(3)
Разлагая стадии ki, 1≤i≤3, в ряды Тейлора и подставляя в первую формулу (3), получим ряд Тейлора для приближенного решения yn+1. Полагая yn=y(tn) и сравнивая ряды для точного и приближенного решений, получим условия третьего порядка точности схемы (3), то есть:
, 
,
, 
.
Положим a, β31 и β32 свободными и исследуем эту систему на совместность. Получим:
,
, (4)
, 
,
где β=β31+β32. Исследуем устойчивость схемы (3) на линейном скалярном уравнении y¢=λy, где смысл комплексного числа λ, Re(λ)<0, – некоторое собственное число матрицы Якоби задачи (1). Применяя (3) для решения этого уравнения, получим yn+1=Q(z)yn, где z=hλ, а функция устойчивости Q(z) записывается следующим образом:
.
Из вида Q(z) следует, что для L-устойчивости схемы (3) необходимо выполнение соотношения a2–a(p1+p3)+β31p3=0. Подставляя сюда коэффициенты (4), получим уравнение a3–3a2+1.5a–1/6=0. Далее, сравнивая представление приближенного и точного решений до членов с h4 включительно, видим, что слагаемые с элементарными дифференциалами f′′′f 3 и f′′f′f 2 в главном члене локальной ошибки будут отсутствовать, если
, 
.
Теперь отсюда и (4) получим набор коэффициентов
, 
, 
,
, 
, 
,
при которых локальная ошибка δn,3 схемы (3) имеет вид
,
где значение a определяется из условия L-устойчивости a3–3a2+1.5a–1/6=0. Это уравнение имеет три вещественных корня. Согласно [1] требование A-устойчивости схемы (3) имеет вид 1/3≤a≤1/0685790, поэтому выбираем корень a=0.435866521508459 .
В жестких задачах поведение ошибки определяется элементарным дифференциалом f′3f [4]. Поэтому при построении оценки аналога глобальной ошибки будем учитывать только первое слагаемое в локальной ошибке. Для контроля точности вычислений и автоматического выбора величины шага интегрирования используем идею вложенных методов. Для этого рассмотрим двухстадийный метод (2) вида
, 
, 
, (5)
где yn вычислено по формуле (3). В численной формуле (5) применяются стадии метода (3), и поэтому она практически не приводит к увеличению вычислительных затрат. Нетрудно видеть, что при коэффициентах b1=0.5(4a–1)/a и b2=0.5(1–2a)/a схема (5) имеет второй порядок точности, а ее локальная ошибка имеет вид δn,2=(6a2−6a+1)h3 f′2f/6+O(h4). Тогда в неравенстве для контроля точности можно применять оценку ошибки εn(jn) вида [4]
. (6)
где c=4·|6a2–6a+1|/|1–12a+36a2–24a3|≈3. При jn=1 оценка εn(jn) будет A-устойчивой, а при jn=2 − L-устойчивой. Теперь неравенство для контроля точности имеет вид
, 
, (7)
где ε − требуемая точность интегрирования, а параметр jn выбирается наименьшим, при котором выполняется неравенство (7). Норма ||ξ|| в (7) вычисляется по формуле
.
В случае выполнения неравенства |yni|<v по i-й компоненте решения контролируется абсолютная ошибка vε, в противном случае контролируется относительная ошибка ε.
3. Последовательный и параллельный алгоритмы интегрирования
Запишем схему (3) в покомпонентной форме, имеем
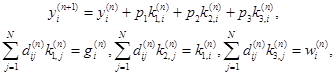(8)
где 
, элементы 
, 
и 
есть компоненты векторов приращений 
, 
и 
, значения 
, 
, 
и 
есть элементы матрицы 
и векторов 
, 
и 
, 
, 
, 
, причем 
при 
и 
при 
. Здесь 
− элементы матрицы Якоби 
задачи (1), вычисленные на решении 
, 
− элементы вектора правой части f(y)
. Применение LU-разложения [2] приводит к системам уравнений для нахождения стадий , и , то есть
, 
, ,
, 
,, (9)
, 
,,
где 
при 
и 
при 
.
В приводимом ниже алгоритме интегрирования используются обозначения программ 
для декомпозиции матрицы и 
для вычисления вектора приращения. С применением обозначения элементов обратной матрицы 
через 
, нормы ошибок 
и 
вычисляются по формулам
, (10)
. (11)
Пусть приближение yn к решению y(tn) задачи (1) вычислено в точке tn с шагом hn. Тогда учитывая, что имеет место εn(jn)=O(hn3), 1≤jn≤2, последовательный алгоритм интегрирования формулируется следующим образом.
Шаг 1. Вычислить матрицу Якоби .
Шаг 2. Сформировать матрицу 
.
Шаг 3. Выполнить декомпозицию матрицы 
.
Шаг 4. Вычислить 
.
Шаг 5. Вычислить 
.
Шаг 6. Вычислить 
.
Шаг 7. Вычислить .
Шаг 8. Вычислить 
.
Шаг 9. Вычислить норму ошибки ||εn(1)|| по формуле (10).
Шаг 10. Вычислить величину q1 по формуле 
||εn(1)||=cε.
Шаг 11. Если q1<1, то есть требуемая точность не достигнута, то вычисляется ||εn(2)|| по формуле (11). В противном случае εn(2) полагается равным εn(1).
Шаг 12. Вычислить значение параметра q2 по формуле 
||εn(2)||=cε.
Шаг 13. Если q2<1, то hn полагается равным q2hn, и происходит повторное вычисление решения – возврат на шаг 2.
Шаг 14. Вычислить приближение к решению в точке tn+1 по формуле (8), то есть
.
Шаг 15. Вычислить значение параметра hn+1 по формуле hn+1=min(q1, q2)hn.
Шаг 16. Выполнить следующий шаг интегрирования.
Для LU-разложения матрицы используется алгоритм с замещением, что дает возможность применять один массив на шаге интегрирования. Далее предположим, что размерность N системы (1) связана с размером p вычислительной системы соотношением N=s·p. Для выберем блочно-строчную схему хранения, dij(n)
proc(j), 
, 
. В результате на каждом процессоре будет размещено s строк матрицы и s элементов вектора y(n). Тогда параллельный аналог (3,2)-метода (3) запишется в виде
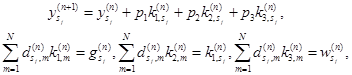(12)
где 
, 
. Параллельные аналоги (9) имеют вид
, 
,
, 
, (13)
, 
,
где , . Сформулируем параллельный алгоритм интегрирования. Для этого введем функции 
и 
, реализующие декомпозицию матрицы и нахождение векторов 
, 
и 
. Для контроля точности (12) используем процессор proc(1). Пусть известно приближение y(n) в точке tn с шагом hn. Тогда для вычисления y(n+1) в точке tn+1 справедлив параллельный алгоритм, в котором на каждом процессоре proc(j) формируется своя j-я часть 
вектора решения.
Шаг 1. В каждом proc(j), , 
: а) выполнить recv
; б) вычислить 
; в) вычислить матрицу Якоби.
Шаг 2. Сформировать матрицу .
Шаг 4. Разложить матрицу .
Шаг 5. Вычислить .
Шаг 6. Вычислить .
Шаг 7. В каждом proc(j), , :
а) выполнить recv
; б) вычислить 
;
в) выполнить send 
.
Шаг 8. В каждом proc(j), , :
а) выполнить recv 
; б) сформировать 
;
в) вычислить 
; г) вычислить 
.
Шаг 9. Вычислить 
.
Шаг 10. В каждом proc(j), , :
а) вычислить 
;
б) вычислить 
;
в) вычислить 
;
г) вычислить 
;
д) выполнить send 
.
Шаг 11. В proc(1): а) выполнить recv 
;
б) определить 
; в) определить 
;
г) вычислить 
; д) если q1<1, то есть требуемая точность не достигнута, то переход на пункт е), иначе εn(2) полагается равным εn(1) и переход на е);
е) вычислить 
; ж) если q2<1, то hn полагается равным q2 hn;
з) выполнить send (hn, rp; 1, …, p). При rp=1 происходит повторное вычисление решения − возврат на шаг 2, при rp=0 − переход на шаг 12.
Шаг 12. В каждом proc (j), , : а) выполнить recv (hn, rp;1);
б) вычислить 
; б) выполнить send 
.
Шаг 13. Выполнить следующий шаг интегрирования.
Необходимость решения жестких задач возникает во многих приложениях. Часто методом прямых уравнения математической физики в частных производных сводятся к жестким системам. Основные тенденции при построении численных методов связаны с расширением их возможностей для решения систем большой размерности. Здесь предложен параллельный алгоритм для вычислительных систем кластерной архитектуры.
Работа выполнена при финансовой поддержке РФФИ (проект 11-01-00106).
Рецензенты:
Богульский Игорь Олегович, д.ф.-м.н., профессор кафедры сопротивления материалов и теоретической механики Института управления инженерными системами Красноярского государственного аграрного университета, г. Красноярск.
Нужин Яков Нифантьевич, д.ф.-м.н., профессор кафедры математического обеспечения дискретных устройств и систем Института фундаментальной подготовки Сибирского федерального университета, г. Красноярск.
Библиографическая ссылка
Новиков Е.А., Ващенко Г.В. ПАРАЛЛЕЛЬНЫЙ (3,2)-МЕТОД РАСЧЕТА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ // Современные проблемы науки и образования. – 2012. – № 6. ;URL: https://science-education.ru/ru/article/view?id=7448 (дата обращения: 20.04.2024).