Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

В рамках реформирования современного российского высшего образования [1; 4; 7; 8] единый государственный экзамен (ЕГЭ) предлагается в качестве одного из критериев, по которым будет оцениваться деятельность высших учебных заведений [6]. Результаты ЕГЭ рассматриваются как критерий оценки качества работы средней школы и качества набора абитуриентов в высшую школу [3; 5; 9]. При реорганизации сети вузов РФ предполагается сокращение их числа и изменение механизма перераспределения средств в государственном секторе образования таким образом, что финансирование вуза будет зависеть от качества сформированного им контингента студентов, то есть от рейтинга вуза по среднему баллу ЕГЭ (mЕ). Такой рейтинг [2], показывающий уровень знаний абитуриентов 2012 г., поступивших на бюджетные места в 491 государственный вуз страны, возглавляют 10 вузов, среди которых 5 социально-экономических (СЭВ), 2 классических (КВ), по одному техническому (ТВ), гуманитарному (ГВ), медицинскому (МВ) и ни одного педагогического (ПВ), архитектурно-строительного (АСВ), аграрного (АВ).

В данной работе проведен многомерный статистический (дисперсионный, корреляционный и кластерный) анализ профильного высшего образования на основе не только рейтинга вузов по среднему баллу ЕГЭ, но и целой системы показателей вступительных испытаний (ПВИ) 2012 г. Статистический анализ проведен в системе Statistica [10].

На основании ПВИ 2012 г. [2] были рассчитаны средние для профильных групп вузов по каждому ПВИ (табл. 1), среди которых, кроме mЕ , приведено также долевое количество абитуриентов (в % от общего количества бюджетных мест), принятых по конкурсу баллов ЕГЭ (NЕ), по олимпиадам (NО), по льготам (NЛ) и по целевому набору (NЦ). Заметим, что подсистема долевых показателей является избыточной, так как NЕ+NЦ+NО+NЛ =100%, что позволяет исключить из рассмотрения одну долевую ПВИ, например NЛ.

Таблица 1 – Профильно-групповые средние ПВИ 2012 г.

В результате проверки ПВИ на корреляционную зависимость выделена наиболее высокозначимая отрицательная корреляция между NЕ и NЦ (коэффициент парной корреляции Пирсона r ≈ -0,921, а ранговый Спирмена R ≈ -0,849). Наличие сильной корреляционной связи между NЕ и NЦ позволяет уменьшить количество долевых ПВИ еще на одну, например, NЦ, связанной с NЕ уравнением линейной регрессии NЦ = 80,525-0,84*NE, и провести дальнейший анализ в трехмерной системе ПВИ: {mЕ, NЕ, NО}.

Согласно λ-критерию Уилкса восемь профильных групп вузов высокозначимо (на уровне значимости р < 0,0005) различаются по совокупности показателей {mЕ, NЕ, NО}. В рамках однофакторного дисперсионного анализа можно оценить их однородность по каждому показателю. Заметим, что в рассматриваемом случае параметрический F-критерий подтверждает выводы рангового критерия Краскела–Уоллиса и медианного теста о высокозначимом (на уровне p < 0,0005) различии между профильными группами для каждого показателя, а использование параметрического апостериорного критерия наименьших значений разности приводит к большему количеству малочисленных объединений профильных однородных групп. При этом можно выделить для каждого показателя однородные (различающиеся незначимо, то есть на уровне значимости р > 0,10) объединения профильных групп, расположенные в порядке убывания групповых средних:

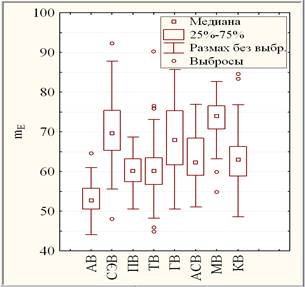
Ø      mЕ (рис. 1): {МВ}, {СЭВ, ГВ}, {АСВ, КВ}, {АСВ, ТВ, ПВ}, {АВ}. Имеется одна пара пересекающихся объединений профильных групп.

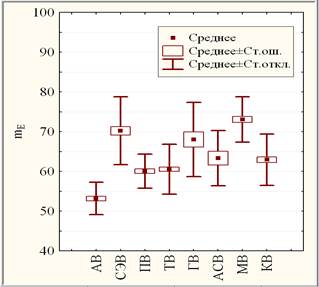
Рис. 1. Непараметрическая (слева) и параметрическая (справа) диаграммы размаха профильных групп вузов по 100-балльной шкале mЕ .

Ø      NЕ: {АСВ, ГВ, КВ, ПВ}, {КВ, ПВ, ТВ}, {ТВ, СЭВ, АВ}, {МВ}. Имеются две последовательные пары пересекающихся объединений профильных групп.

Ø      NО: {СЭВ, ТВ}, {ТВ, КВ, ГВ}, {ГВ, МВ, АСВ, ПВ, АВ}. Имеются две последовательные пары пересекающихся объединений профильных групп.

В связи с тем что неоднородность групп вузов оценивалась как с помощью параметрического F-критерия, так и с помощью рангового критерия Краскела–Уоллиса, наряду с параметрическими (рис. 1, справа) числовыми характеристиками (среднее и стандартное отклонение) приводятся и непараметрические (рис. 1, слева) их аналоги (медиана и квартили) для профильных групп вузов по mЕ.

Наличие однородных объединений профильных групп вузов по каждому показателю mЕ, NЕ, NО допускает проведение их кластеризации в трехмерной системе ПВИ: {mЕ, NЕ, NО}. В качестве меры близости выбрано расстояние городских кварталов, а в качестве правила объединения двух кластеров использован метод Уорда. Методом иерархической кластеризации построена дендрограмма (рис. 2, слева). В зависимости от выбора расстояния объединения можно получить соответствующее число кластеров. Так, например, расстоянию объединения, равному 1,2 (красная пунктирная вертикальная прямая), соответствуют 5 кластеров: 1 составной (АСВ+КВ+ПВ+ТВ) и 4 монокластера (ГВ), (АВ), (СЭВ), (МВ), а расстоянию объединения, равного 2, соответствуют 4 кластера за счет объединения (АСВ+КВ+ПВ+ТВ) с (ГВ). Наряду с методом древовидной кластеризации применен также метод K-средних, проводящий классификацию объектов (профильных групп вузов) по заданному количеству кластеров. Предлагается 5-кластерная модель профильных групп вузов, согласно λ-критерию Уилкса высокозначимо (на уровне значимости р < 0,000005) различающая 5 кластеров профильных групп вузов по совокупности {mЕ, NЕ, NО}. Кластерные графики средних профильных групп вузов изображены на рис. 2 справа.

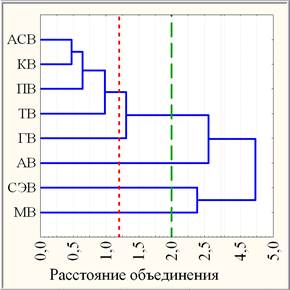
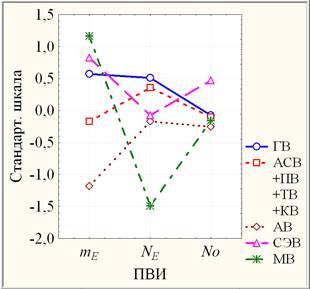
Рис. 2. Дендрограмма (слева) и кластерные графики (справа) средних профильных групп вузов по стандартизированной шкале {mЕ, NЕ, NО}.

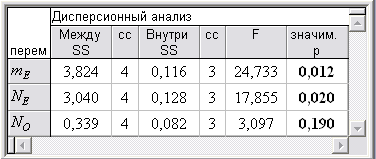
Алгоритм метода K-средних перемещает объекты в разные кластеры с целью минимизации изменчивости внутри кластеров и максимизации изменчивости между кластерами, оценивая качество кластеризации профильных групп вузов по каждому ПВИ посредством параметрического дисперсионного анализа (табл. 2) как статистически значимое (на уровне значимости 0,01 < р < 0,05) для mЕ и NЕ.

Таблица 2 – Результаты дисперсионного анализа кластеризации профильных групп вузов по каждому ПВИ

На основании рис. 2 в трехмерной системе ПВИ: {mЕ, NЕ, NО} можно провести качественную классификацию профильных групп вузов в номинальной шкале измерений (табл. 3), полагая в качестве уровня «Средний» – стандартизированный интервал (–0,3; +0,3) для показателей. Аномально высокие значения (> +1,0) определяют уровень «Лидер», а аномально низкие значения (< -1,0) определяют уровень «Аутсайдер». Промежуточные значения между средними и аномальными определяют уровень «Выше среднего» и «Ниже среднего» соответственно. Таким образом, выделяются 5 объединений профильных групп.

Таблица 3 – Качественная классификация профильных групп вузов

Результаты качественной классификации профильных групп вузов представлены на рис. 3 в виде образной формы «птицы потенциального профильного высшего образования», обладающей «гуманитарной» головкой с повышенным уровнем mЕ и NЕ, правым «медико-целевым» крылом, лидирующим по mЕ и NЦ, левым «социально-экономическим» крылом с повышенным уровнем mЕ и NО, разнопрофильным туловищем (АСВ+ПВ+ТВ+КВ) среднего уровня по всем показателям и «аграрным» хвостом с сильно пониженным уровнем mЕ.

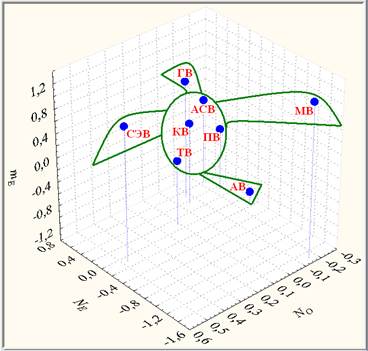
Рис. 3. Диаграмма рассеяния профильно-групповых средних в системе {mЕ, NЕ, NО} ПВИ 2012 г.

На основании ПВИ [2] в трехмерной системе {mЕ, NЕ, NО} можно оценить тренд динамики профильно-групповых средних и его значимость (рис. 4).

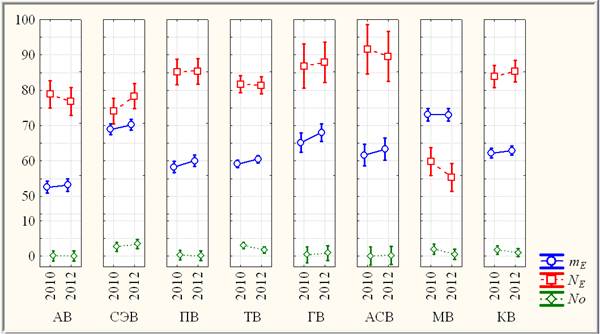
Рис. 4. Диаграмма рассеяния профильно-групповых средних 2010 и 2012гг. с 95% доверительными интервалами в трехмерной системе ПВИ {mЕ, NЕ, NО}.

К сожалению, ограниченность базы данных 2011 г. (включены вузы, принявшие не менее 200 человек по результатам ЕГЭ) уменьшает общее количество охваченных исследованием вузов более чем на 100 по сравнению с 2010 и 2012 гг., а по некоторым профильным группам вузов (СЭВ и МВ) уменьшает их число в 2 раза, что делает их сравнение некорректным. Поэтому далее профильно-групповые средние в трехмерной системе ПВИ {mЕ, NЕ, NО} сравниваются по 2010 и 2012 гг.

Для каждого показателя оценим тренд динамики профильно-групповых средних и его значимость на основании параметрического t-критерия (уровень значимости рt) и непараметрического U-критерия Манна-Уитни (уровень значимости рМ-У) для двух независимых групп:

v        mЕ: положительная динамика у всех профильных групп, кроме МВ. Однако значимой в разной степени оценивается положительная динамика почти на 2 балла у ПВ (уровень статистической значимости 0,01< рt ≈0,03< 0,05 и 0,01<рМ-У ≈0,04< 0,05) и почти на 1,5 балла у ТВ (уровень слабой значимости 0,01< рt ≈0,07< 0,05 и уровень статистической значимости 0,01<рМ-У ≈0,03< 0,05). Остальные случаи оценивается как не значимые (рt > 0,1; рМ-У > 0,1), в том числе наибольшая положительная динамика у ГВ (увеличение группового среднего почти на 3 балла).

v        NЕ: положительная не значимая (рt > 0,1; рМ-У > 0,1) динамика у СЭВ (наибольшая почти на 4%), ПВ, ГВ, КВ и отрицательная не значимая (рt > 0,1; рМ-У > 0,1) динамика у МВ (наибольшая почти на 4,5%), АСВ, ТВ, АВ.

v        NО: положительная не значимая (рt > 0,1; рМ-У > 0,1) динамика у СЭВ (наибольшая почти на 1%), ГВ, АСВ и отрицательная не значимая (рt > 0,1; рМ-У > 0,1) динамика у остальных , в том числе у МВ и ТВ (> 1%).

Выводы

1. Выявлена высокозначимая отрицательная корреляция между долевыми количествами абитуриентов, принятых по конкурсу баллов ЕГЭ и по целевому набору.
2. В трехмерной системе ПВИ 2012 г. (средний балл ЕГЭ, долевые количества абитуриентов, принятых по конкурсу баллов ЕГЭ и по олимпиадам) сделан вывод о высокозначимом различии восьми профильных групп вузов по совокупности показателей, оценена их однородность по каждому показателю в рамках дисперсионного анализа.
3. Дисперсионный анализ восьми профильных групп вузов по совокупности трех показателей позволил выделить пять однородных объединений и представить результаты в виде образной формы «птицы потенциального профильного высшего образования», обладающей «гуманитарной» головкой, правым (целевым) «медицинским» крылом, левым (олимпиадным) «социально-экономическим» крылом, «аграрным» хвостом и разнопрофильным туловищем из оставшихся четырех профильных групп вузов.
4. Для каждого показателя оценен тренд динамики профильно-групповых средних и его значимость. Статистически значимой оценена только положительная динамика по среднему баллу ЕГЭ почти на 2 балла у ПВ и почти на 1,5 балла у ТВ.
5. Результаты подобной кластеризации вузов могут быть учтены в рамках проходящей реформы высшего образования, например при принятии решений об оптимизации сети вузов и их финансировании.

Работа выполнена в рамках государственного задания «Наука» № 1.604.2011 и поддержана ФЦП «Научные и научно-педагогические кадры инновационной России» по контрактам П691.

Рецензенты

Трифонов Андрей Юрьевич, д.ф.-м.н., профессор кафедры высшей математики и математической физики, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет», г. Томск.

Арефьев Константин Петрович, д.ф.-м.н., профессор кафедры высшей математики, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет», г. Томск.