В современных условиях особое значение приобретает повышение эффективности применения всего комплекса средств аэродромно-технического обеспечения (АТО) полётов, сокращение материальных и трудовых затрат на подготовку ВС к полётам, их обслуживание, хранение и сбережение, что существенно влияет на боевую готовность. Обеспечение безопасности полётов неразрывно связано с состоянием, техническими характеристиками и возможностями средств АТО полётов, в частности, средств эвакуации и буксировки ВС. Роль этих средств при ведении боевых действий возрастает в ещё большей степени [5].
В то же время существующий в настоящее время методический аппарат не позволяет в полной мере проводить адекватную оценку эффективности использования разрабатываемых средств наземного транспортирования воздушных судов, что указывает на необходимость его модификации [3].
Конструкция обеспечивает эффективную всесезонную и всепогодную эксплуатацию буксировщика, представлена на рис. 1. Аэродромная буксировочная система с автоматически изменяемым сцепным весом, в зависимости от силы сопротивления качению ВС [1,2], содержит тягово-сцепное устройство, обеспечивает догрузку тягача в зоне опорного периметра, что способствует более равномерному её распределению по ведущим мостам.

Рис.1. Автоматическое тягово-сцепное догружающее устройство
Проведенные экспериментальные исследования и полученные тяговые характеристики агрегата на различных аэродромных покрытиях показали более высокие результаты. При догрузке тягача в зоне опорного периметра весом самолета, приходящимся на его переднюю стойку величиной 30 кН, тяговая мощность агрегата увеличивается в среднем на 56 %.
При этом коэффициент буксования на режиме максимальной тяговой мощности уменьшается на всех покрытиях в среднем на 55,2 %, а удельный эффективный расход топлива уменьшается в среднем на 34,7 %.
Буксировочная система, состоящая из аэродромного тягача и ВС, оборудованная автоматическим увеличителем сцепного веса, является сложной механической системой. Для ее аналитических исследований создана двухмассовая математическую модель, отражающая взаимодействие элементов структурной схемы между собой и поведение системы в целом (рис.2).
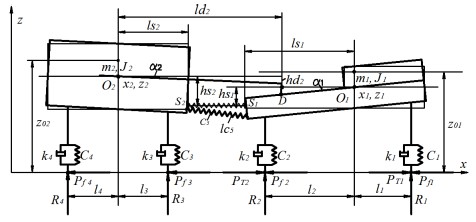
Рисунок 2. Расчетная схема двухмассовой буксировочноой системы
С учетом продольной симметрии комплекса принимается плоская расчетная схема. Положение тягача описывается координатами x1, z1 его центра масс O1 и углом наклона α1 продольной оси к горизонту. Аналогично для летательного аппарата используются координаты x2, z2, α2. Инерционность элементов буксировочной системы учитывается массами тягача m1 и летательного аппрата m2, а также их моментами инерции относительно центров масс J1, J2.
Оба объекта опираются на горизонтальное основание аэродрома через упруго-диссипативные элементы Ci, ki (i = 1...4), представляющие колеса и подвески тягача и летательного аппарата. Недеформированному состоянию упругих элементов Ci соответствуют высоты центров масс z01, z02 и нулевые значения углов наклона рассматриваемых объектов (α1=α2=0). Взаимодействие тягача и ВС с опорной поверхностью учитывается нормальными реакциями RZi, силами сопротивления качению Pfi и силами тяги ведущих мостов тягача PТi. Зависимость сил сопротивления качению от норамальных реакций учитывается соотношениями Pfi = RZi ×fi , где fi - коэффициенты сопротивления качению колес ВС и тягача.
Тягач и ВС взаимодействуют между собой через буксировочное и догружающее устройства.
Буксирующая сцепка представлена на схеме упругим элементом С5, шарнирно соединенным с тягачем и буксиром. Точки шарнирного крепления буксирной сцепки к тягачу и воздушному судну обозначены через S1 и S2 соответственно. Сцепка не накладывает геометрических ограничений на перемещения и поэтому число степеней свободы системы не снижает.
Догружающее устройство, жестко скрепленное с прицепом (ВС), рассматривается на схеме как часть летательного аппарата, оно контактирует с тягачом в точке D. Этот контакт в процессе буксировки не нарушается, что определяет геометрические ограничения на взаимные перемещения тягача и прицепа. Таким образом, догружающее устройство уменьшает число степеней свободы системы.
Для описания динамики буксировочной системы используются уравнения равновесия тягача и прицепа. Поскольку система оказывается статически неопределимой, то уравнения равновесия дополняются геометрическими взаимосвязями между ее частями и физическими условиями, вытекающими из свойств упругих и диссипативных элементов (рис. 3,4).
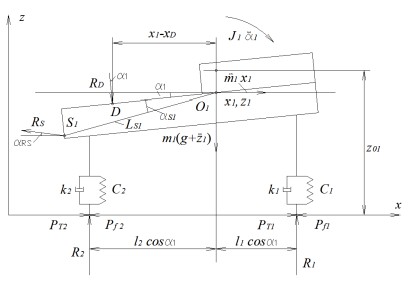
Рисунок 3. Схема сил, приложенных к тягачу
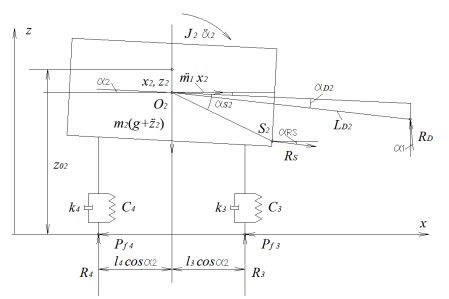
Рисунок 4. Схема сил, приложенных к ВС
Уравнения равновесия тягача, записанные методом кинетостатики, представлены соотношениями (1) - (3) (рис. 3), а ВС - соотношениями (4) - (6) (рис. 4)
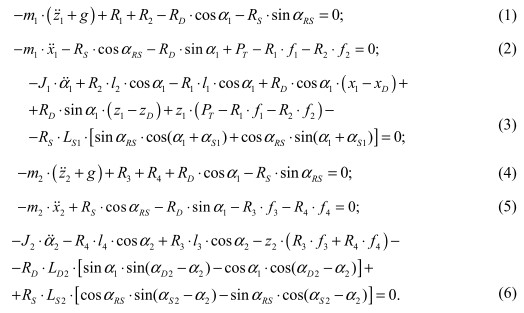
где RS, RD - реакции на тягач со стороны буксирующего и догружающего устройств соответственно; XD - горизонтальное расстояние от центра масс до точки приложения догружающего усилия; РТ = РТ1+РТ2 - суммарная сила тяги переднего (РТ1) и заднего (РТ2) мостов тягача.
В качестве физических условий используются данные о жесткости и диссипативных свойствах колес и подвесок тягача и ВС. С учетом этих свойств соотношения между вертикальными реакциями и деформацией упругих элементов выражаются формулами
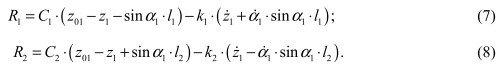
Помимо этого учитывается взаимосвязь между деформацией сцепного устройства и силой RS
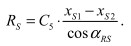 (9)
(9)
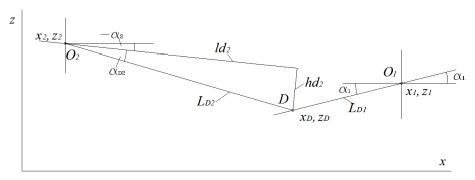
Рисунок 5. Взаимосвязь между положением тягача и прицепа
Соотношение между координатами α1, и α2, обусловленная наличием догружающего устройства, определяется из геометрических соображений (рис. 5)
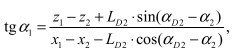 (10)
(10)
где 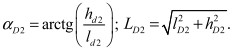
С учетом малости α1 и α2 последнее соотношение приводится к виду
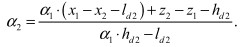 (11)
(11)
Анализ динамики буксировочной системы заключается в решении системы уравнений (1) - (11) на характерных режимах работы по транспортировке ВС. Такими характерными режимами являются трогание с места, разгон и торможение. Равномерное движение специально не рассматривается, так как его параметры совпадают с параметрами конца разгона.
Во время трогания с места величина суммарной силы тяги определяется воздействием водителя тягача на педали газа и сцепления. Характер этого воздействия может быть весьма разнообразным, но в целом он приводит к росту РТ , который с приемлемым приближением можно считать линейной функцией времени. То есть на этапе трогания с места за начальные условия принимаются нулевые значения перемещений, скоростей и ускорений, а РТ описывается уравнением вида
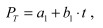 ,
,
где a1 - константа равная силе сопротивления качению всех колес буксировочной системы в статическом положении; b1 - константа, характеризующая интенсивность роста крутящего момента на ведущих колесах тягача.
Трогание с места заканчивается при выходе двигателя тягача на его внешнюю характеристику.
Считается, что разгон происходит при полной подаче топлива, то есть на внешней скоростной т характеристике двигателя. Если эту харавтеристку аппроксимировать линейной функцией, то РТ на этапе разгона примет вид
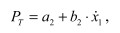 ,
,
где a2, b2 - константы, определяемые параметрами внешней скоростной характеристики двигателя тягача.
За начальные условия разгона принимаются конечные параметры этапа трогания. Этап разгона считается завершенным, если продольное ускорение упадет ниже некоторого заданного уровня.
Наибольший интерес представляет экстренное торможение, интенсивность которого определяется условиями сцепления колес с опорой, это позволяет сделать допущение о постоянстве тормозной силы на этом этапе.
PТ = а3.
где a3 - константа, определяемая состоянием поверхности аэродрома.
Начальные условия торможения совпадают с конечными параметрами разгона, а признаком окончания процесса является нулевая скорость движения.
Решение системы уравнений (1) - (11) для тягачей и ВС с различными параметрами позволит правильно определить конструкцию буксировочной системы и определить границы ее эффективного применения.
Рецезенты:
Федюнин П. А., доктор технических наук, профессор, нач. кафедры управления воинскими частями С и РТО Военного Учебно-научного центра Военно-воздушных сил (Военно-воздушная академия им. проф. Н. Е. Жуковского и Ю. А. Гагарина), г. Воронеж.
Спиридонов Е. Г., доктор технических наук, доц., профессор кафедры криогенной техники, систем кондиционирования и метрологического обеспечения экологии Военного Учебно-научного центра Военно-воздушных сил (Военно-воздушная академия им. проф. Н. Е. Жуковского и Ю. А. Гагарина), г. Воронеж.
Библиографическая ссылка
Великанов А.В. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДВУХМАССОВОЙ АЭРОДРОМНОЙ БУКСИРОВОЧНОЙ СИСТЕМЫ С ИСПОЛЬЗОВАНИЕМ УРАВНЕНИЙ КИНЕТОСТАТИКИ // Современные проблемы науки и образования. 2012. № 5. ;URL: https://science-education.ru/ru/article/view?id=7333 (дата обращения: 06.03.2026).



