Введение
В авиации актуальной является проблема обеспечения безопасности полетов, а именно прогнозирования и предотвращения авиационных происшествий, приводящих как к человеческим жертвам, так и к материальным потерям. Одним из основных факторов опасности, которые приводят к авиационным происшествиям, является фактор, отвечающий различным отказам и неисправностям функциональных систем планера. Исходя из данных российской статистики, доля авиационных происшествий по причинам отказа авиатехники составляет около 20% (для авиационных инцидентов эта доля – около 70%) [1; 5]. При этом около 60% инцидентов, вызванных неисправностями авиатехники, приходится на отказы двигателей. Это свидетельствует о необходимости внедрения эффективных и оптимальных управленческих решений в целях обеспечения безопасности полетов. Настоящая работа посвящена описанию имитационной модели (представленной в терминах систем массового обслуживания – СМО) системы принятия управляющих решений для обеспечения оптимального уровня безопасности полётов воздушных судов с учётом платы за управление и потерь, отвечающих повреждениям и отказам газотурбинных двигателей (ГТД).
Постановка задачи
В работе рассматривается модель, описывающая возникновение отказов (неисправностей) в авиационных ГТД. При этом принято допущение о том, что интенсивность возникновения отказов и неисправностей снижается для каждого из двигателей линейно в зависимости от уровня затрат на управляющее воздействие. Коэффициент пропорциональности в этой линейной зависимости определяется экспертно.
Неисправности двигателя могут быть как диагностируемые, так и недиагностируемые. В представленной модели во введённых терминах выявление неисправностей (во время плановой диагностики или во время эксплуатации двигателя) рассматривается как обслуживание. Но также с положительной вероятностью на каждом ненулевом интервале времени могут возникнуть невыявленные за это время неисправности. Поэтому такие неисправности могут приводить к поломке и повреждениям других элементов двигателя, т.е. появлению новых дефектов и возникновению новых отказов. В результате чего образуется очередь из отказов (неисправностей).
Приведём формальную математическую постановку рассматриваемой проблемы в форме задачи об оптимальном управлении. Для этого в терминологии СМО запишем:
![]() – поток возникновения
новых отказов, который включает: входной поток заявок, «размножение»
неисправностей, управляющее воздействие на интенсивность возникновения заявок;
– поток возникновения
новых отказов, который включает: входной поток заявок, «размножение»
неисправностей, управляющее воздействие на интенсивность возникновения заявок;
![]() – поток заявок, обслуженных
к моменту времени t
неисправностей (т.е. здесь число выявленных неисправностей в ходе эксплуатации
или диагностики ГТД);
– поток заявок, обслуженных
к моменту времени t
неисправностей (т.е. здесь число выявленных неисправностей в ходе эксплуатации
или диагностики ГТД);
![]() – процесс управления
размножением заявок в очереди;
– процесс управления
размножением заявок в очереди;
![]() – очередь заявок (число
ещё не выявленных неисправностей).
– очередь заявок (число
ещё не выявленных неисправностей).
Взаимосвязь этих процессов
представлена в виде СМО, в которой роль заявок играют неисправности ГТД. Таким
образом, в работе рассматривается СМО с длиной очереди – процессом ![]() , входным поток заявок –
, входным поток заявок – ![]() и выходным (обслуживанием) –
и выходным (обслуживанием) – ![]() при
при ![]() (рис.
1).
(рис.
1).
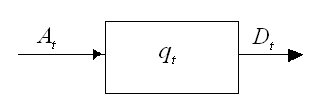
Рис. 1. Общая схема СМО.
Справедливо следующее балансовое соотношение:
![]() , (1)
, (1)
с
начальными значениями ![]() и
и ![]() .
.
Данные процессы рассматриваются на стохастическом базисе ![]() , где вероятностное пространство
, где вероятностное пространство ![]() , снабженное неубывающим потоком
, снабженное неубывающим потоком ![]() -алгебр
-алгебр ![]() ,
,
![]() , при
, при ![]() ,
являющимся непрерывным справа, т.е.
,
являющимся непрерывным справа, т.е. ![]() , где
, где ![]() . Для представленной системы
предполагается, что входной поток не является стандартным пуассоновским.
Считающий процесс числа поступающих заявок
. Для представленной системы
предполагается, что входной поток не является стандартным пуассоновским.
Считающий процесс числа поступающих заявок ![]() является
управляемым точечным. Процесс обслуживания
является
управляемым точечным. Процесс обслуживания ![]() –
предполагается точечным с интенсивностью, отвечающей СМО с бесконечным числом
приборов [2].
–
предполагается точечным с интенсивностью, отвечающей СМО с бесконечным числом
приборов [2].
Рассматривается задача оптимального
управления входным потоком в предположениях, что данная модель отвечает
ситуации, при которой «выгодно» уменьшение средней длины очереди (в результате
увеличения управляющего воздействия), в условиях пропорциональной платы за
управление. Эта задача допускает формальное математическое представление с
соответствующим функционалом потерь в так называемых семимартингальных
терминах. В этих терминах (называемых также траекторными) рассматриваемый
процесс – ![]() , является специальным
семимартингалом и допускает разложение
, является специальным
семимартингалом и допускает разложение ![]() ,
где
,
где ![]() – локальный мартингал, а
– локальный мартингал, а ![]() – непрерывный процесс конечной
вариации с
– непрерывный процесс конечной
вариации с
![]() (2)
(2)
Здесь в соответствии с соотношением (1), ![]() и
и ![]() –
компенсаторы в соответствующих разложениях Дуба-Мейера, см. например [3],
точечных процессов
–
компенсаторы в соответствующих разложениях Дуба-Мейера, см. например [3],
точечных процессов ![]() и
и ![]() :
:
![]() ,
(3)
,
(3)
![]() ,
(4)
,
(4)
где
![]() и
и ![]() –
неубывающие непрерывные процессы,
–
неубывающие непрерывные процессы, ![]() и
и ![]() – мартингалы.
– мартингалы.
Обслуживание каждой заявки отдельно
происходит с постоянной интенсивностью, и поэтому общая его интенсивность
пропорциональна числу заявок в очереди с некоторым коэффициентом ![]() :
:
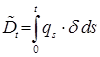 ,
(5)
,
(5)
здесь коэффициент ![]() играет роль
интенсивности каждого из обслуживающих приборов, которые предполагаются в
рассматриваемом приближении эквивалентными и превосходящими количественно
возможную максимальную длину очереди заявок, что и соответствует предположению
о бесконечном их числе [4; 6].
играет роль
интенсивности каждого из обслуживающих приборов, которые предполагаются в
рассматриваемом приближении эквивалентными и превосходящими количественно
возможную максимальную длину очереди заявок, что и соответствует предположению
о бесконечном их числе [4; 6].
Тогда для представленных процессов справедлива следующая интегральная запись:
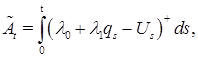 (6)
(6)
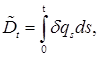 (7)
(7)
![]() (8)
(8)
где ![]() – интенсивность входного потока
заявок (неисправностей),
– интенсивность входного потока
заявок (неисправностей), ![]() – интенсивность
размножения заявок (неисправностей) внутри очереди,
– интенсивность
размножения заявок (неисправностей) внутри очереди, ![]() –
интенсивность обслуживания заявок,
–
интенсивность обслуживания заявок, ![]() – управляющий
элемент входным потоком заявок, положительная часть числа
– управляющий
элемент входным потоком заявок, положительная часть числа ![]() , если
, если ![]() и
и
![]() , если
, если ![]() .
.
При рассмотрении задачи об оптимальном управлении определим функционал потерь:
![]() ,
(9)
,
(9)
где ![]() – это стоимость единичного
управляющего воздействия, производимого за единицу времени t и обеспечивающего снижение
интенсивности возникновения новых неисправностей на величину
– это стоимость единичного
управляющего воздействия, производимого за единицу времени t и обеспечивающего снижение
интенсивности возникновения новых неисправностей на величину ![]() ,
, ![]() –
управляющее воздействие (символ
–
управляющее воздействие (символ ![]() означает
математическое ожидание). Коэффициент
означает
математическое ожидание). Коэффициент ![]() ,
являясь эмпирическим, первоначально определяется экспертно.
,
являясь эмпирическим, первоначально определяется экспертно.
В представленной модели вероятность того, что в двигателе
существуют невыявленные неисправности или дефекты, с которыми он может
эксплуатироваться, строго положительна при заданных ограничениях для параметров
![]() ,
, ![]() ,
,
![]() . Это может вызвать более
многочисленные повреждения ГТД, вследствие чего может даже наступить отказ и
остановка двигателя, и в результате ремонт и замена деталей двигателя будут
более дорогостоящими, что определяется слагаемым
. Это может вызвать более
многочисленные повреждения ГТД, вследствие чего может даже наступить отказ и
остановка двигателя, и в результате ремонт и замена деталей двигателя будут
более дорогостоящими, что определяется слагаемым ![]() в
правой части формулы (6) как показатель размножения заявок в очереди
в
правой части формулы (6) как показатель размножения заявок в очереди ![]() с интенсивностью
с интенсивностью ![]() для каждой заявки.
для каждой заявки.
В задаче необходимо определить некоторое управляющее
воздействие ![]() , которое снижает интенсивность
поступления новых заявок (неисправностей) на величину
, которое снижает интенсивность
поступления новых заявок (неисправностей) на величину ![]() ,
при установленном коэффициенте
,
при установленном коэффициенте ![]() и соответствующей
плате за управление. Таким образом, необходимо решить задачу оптимального
управления в форме
и соответствующей
плате за управление. Таким образом, необходимо решить задачу оптимального
управления в форме
![]() ,
(10)
,
(10)
где
функционал потерь ![]() определён в (9).
определён в (9).
В результате решения задачи (10) устанавливается уровень управляющего воздействия, позволяющий минимизировать затраты на обслуживание и ремонт ГТД при сохранении максимальной его работоспособности.
В стационарном состоянии математическое ожидание правой части
выражения (1) должно быть постоянным. Это означает, что при ![]() и оптимальном управлении
производная математических ожиданий правой части стремится к нулю. То есть,
выполняется соотношение:
и оптимальном управлении
производная математических ожиданий правой части стремится к нулю. То есть,
выполняется соотношение:
![]() (11)
(11)
где ![]() – средняя длина очереди в
стационарном состоянии
– средняя длина очереди в
стационарном состоянии
![]() (12)
(12)
Из выражения (11) получаем, что
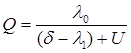 (13)
(13)
Подставляя ![]() в функционал потерь
(9) с учетом (12), определяется такое значение
в функционал потерь
(9) с учетом (12), определяется такое значение ![]() ,
которое при заданном коэффициенте
,
которое при заданном коэффициенте ![]() , определяющем
стоимость единичного управляющего воздействия, производимого за единицу времени
t, на
временном интервале
, определяющем
стоимость единичного управляющего воздействия, производимого за единицу времени
t, на
временном интервале ![]() , минимизирует средние
затраты
, минимизирует средние
затраты ![]() . Для этого найдём минимум
полученной теоретической функции, сделав необходимые преобразования:
. Для этого найдём минимум
полученной теоретической функции, сделав необходимые преобразования:
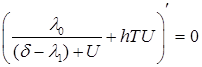 ,
(14)
,
(14)
откуда получаем:
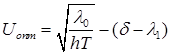 . (15)
. (15)
Полученное аналитически значение оптимального уровня
управляющих воздействий ![]() (с их
стоимостью
(с их
стоимостью ![]() ), вообще говоря, является
оптимальным лишь асимптотически. На переходных режимах (при отсутствии
стационарности интенсивности входных потоков и потоков обслуживания)
применяется метод стохастического имитационного моделирования, который
позволяет скорректировать значение уровня
), вообще говоря, является
оптимальным лишь асимптотически. На переходных режимах (при отсутствии
стационарности интенсивности входных потоков и потоков обслуживания)
применяется метод стохастического имитационного моделирования, который
позволяет скорректировать значение уровня ![]() .
.
Ниже приведён иллюстративный пример для демонстрации сопоставления аналитического и имитационного (корректирующего на переходных режимах) методов определения оптимального управляющего воздействия.
На рисунках 2, 3 с целью иллюстрации процедуры управления в
СМО приведены значения процесса ![]() в зависимости
от выбора параметра
в зависимости
от выбора параметра ![]() (
(![]() =0,
=0,
![]() =1 и
=1 и ![]() =5
соответственно) при фиксированных значения параметров
=5
соответственно) при фиксированных значения параметров ![]() 10,
10,
![]() 5,
5, ![]() 1;
1;
![]() 2.
2.
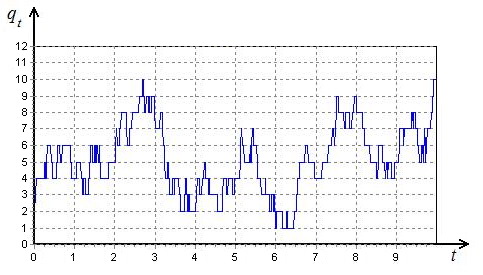
Рис. 2. Длина
очереди ![]() при нулевом управлении (
при нулевом управлении (![]() =0).
=0).
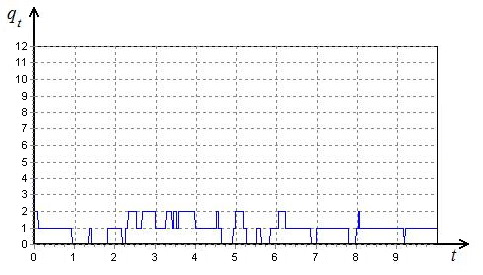
Рис. 3. Длина
очереди ![]() при
при ![]() =5.
=5.
Как видно из графиков, изображенных на рисунках 3–4, с
увеличением управляющего воздействия происходит уменьшение средней длины
очереди ![]() .
.
Далее приводится нахождение оптимального уровня управляющих
воздействий. При построении компьютерной модели было взято 10000 очередей
(процессов) ![]() , подсчитано их среднее (за
временной интервал равный 10), которое подставили в функционал потерь
, подсчитано их среднее (за
временной интервал равный 10), которое подставили в функционал потерь ![]() . На рисунке 5 представлен график
зависимости значения функционала потерь от управляющего воздействия.
. На рисунке 5 представлен график
зависимости значения функционала потерь от управляющего воздействия.
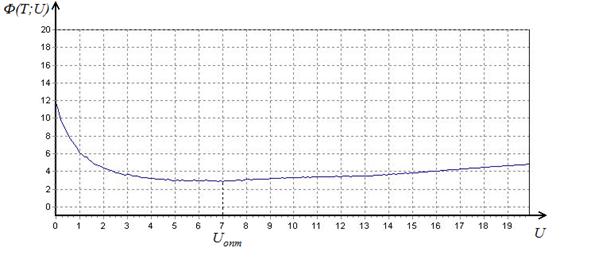
Рис. 4. График функционала потерь, полученного в результате имитационного моделирования.
По результатам имитационного моделирования получено
оптимальное значение параметра ![]() :
: ![]() 7, достигаемое при
7, достигаемое при ![]() 10,
10, ![]() 12,
12,
![]() 1,
1, ![]() 2,
2,
![]() 0,02. Для аналогичных параметров
было вычислено теоретическое оптимальное значение согласно формуле (15):
0,02. Для аналогичных параметров
было вычислено теоретическое оптимальное значение согласно формуле (15): ![]() 6,74. Значение параметра
6,74. Значение параметра ![]() , полученное в результате
компьютерного моделирования, отличается от теоретического
, полученное в результате
компьютерного моделирования, отличается от теоретического ![]() на величину, равную 0,26, что
показывает адекватность имитационной модели.
на величину, равную 0,26, что
показывает адекватность имитационной модели.
Заключение
Таким образом, была рассмотрена модель системы принятия
управляющих решений для обеспечения (или поддержания) оптимального уровня
безопасности полётов воздушных судов с учётом платы за управление и потерь,
отвечающих повреждениям и отказам ГТД. Но данную модель с введённым
функционалом потерь без дополнительных изменений можно перенести на уменьшение
отказов других функциональных
систем планера. При этом изменятся лишь экспертно и статистически
определяемые значения параметров h и интенсивностей ![]() ,
,
![]() ,
, ![]() .
.
Работа выполнена в рамках федеральной целевой программы «Научные и научно-педагогические кадры инновационной России» на 2009-2013, а также при поддержке Министерства образования и науки РФ в рамках постановления правительства РФ № 218.
Рецензенты
Андреев А.С., д.ф.-м.н., профессор, зав. кафедрой информационной безопасности и теории управления, декан факультета математики и информационных технологий, ФГБОУ ВПО «Ульяновский государственный университет», г. Ульяновск.
Кемер А.Р., д.ф.-м.н., профессор кафедры прикладной математики, ФГБОУ ВПО «Ульяновский государственный университет», г. Ульяновск.
Библиографическая ссылка
Логинов В.Р., Бутов А.А., Волков М.А., Шаров В.Д. СИСТЕМА ПРИНЯТИЯ УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ ДЛЯ ОБЕСПЕЧЕНИЯ ОПТИМАЛЬНОГО УРОВНЯ БЕЗОПАСНОСТИ ПОЛЁТОВ ВС // Современные проблемы науки и образования. 2012. № 5. ;URL: https://science-education.ru/ru/article/view?id=7326 (дата обращения: 01.01.2026).



