Проблемой размещения элементов на кристалле так же, как и проблемой соединения между собой этих элементов, занимается такое направление в компьютерной науке, как проектирование СБИС (VLSI Design). Задача проектирования СБИС является актуальной, т.к. в настоящее время перед производителями компьютерных комплектующих стоят задачи увеличения производительности компьютеров. Этапы проектирования СБИС представлены в [11]. В данной статье рассматриваются второй и третий этапы проектирования.
Целью работы является решение задачи планирования и разработка эффективного алгоритма для решения задачи трассировки СБИС с применением процедур генетического алгоритма.
1. Методы решения задач при проектировании СБИС
Известны разнообразные схемы эволюционных вычислений для решения задачи планирования СБИС [2]. В работе [3] отмечено, что ГА являются затратными в плане используемой памяти. В [10] для решения задачи планирования СБИС используется меметический алгоритм. В [9] для решения задачи планирования СБИС применяют дифференциальную эволюцию (ДЭ). В [4] задачу планирования СБИС решают с помощью муравьиного алгоритма.
В настоящее время из-за высокого уровня сложности современных микросхем (особенно БИС и СБИС) к автоматизированному проектированию СБИС, продукты компании Mentor Graphics и Cadence позволяют решать сколь угодно сложные задачи. Однако смещение акцента с последовательной бесконфликтной прокладки проводников на сначала стопроцентную разводку с конфликтами, затем оптимизирующуюся для уменьшения количества конфликтов, перевело алгоритмы, лежащие в основе пакетов проектирования, из класса последовательных в класс оптимизационных, что, как выяснилось, оказывает колоссальное влияние на качество разводки [8]. Качественная разводка проводников зависит также от качественного размещения элементов на кристалле.
Следовательно, задачи планирования и автоматической трассировки на сегодняшний день не решены полностью, так как эти задачи NP-трудные, оптимизационные, и построить универсальный алгоритм невозможно.
2. Постановка задачи проектирования СБИС
Задача проектирования СБИС сводится к квадратичной задаче о назначениях [5]. Эта задача NP-трудная.
Рассматривается задача размещения функциональных элементов (модулей) на кристалле. Имеется структурная схема, на которой показаны взаимное расположение модулей и соединения между ними. Заданы возможные позиции (комнаты) для размещения модулей. Известны трассы между позициями для прокладки проводников. Необходимо разместить функциональные элементы (модули) по одному в каждую позицию таким образом, чтобы:
1. связи прокладывались по установленным трассам;
2. суммарная длина связей была минимальной;
3. площадь кристалла была минимальной при заданных технологических ограничениях.
При этом G (V,E) - граф связей, который является интерпретацией структурной схемы, где V - число вершин графа, E - число ребер. Вершинами в графе G являются модули, ребрами - соединения между модулями; К= {1,...,n} - возможные позиции (комнаты) для размещения модулей.
В данной статье для решения задачи проектирования СБИС используется подход, предложенный C. Zhuang, K. Sakanushi, L. Jin, Y. Kajitani (Япония) [11].
Дано: M={1,...,n} - множество прямоугольников (модулей); K={1,...,n} - возможные позиции (комнаты) для размещения прямоугольников (модулей).
Найти размещение прямоугольников по комнатам плана на кристалле, при котором площадь кристалла была бы минимальной при требуемых технологических ограничениях (1)-(3).
Дано: кристалл с размещенными на нём прямоугольниками (модулями); структурная схема S, на которой заданы взаимное расположение модулей и соединения между ними.
Требуется: соединить модули на кристалле таким образом, чтобы площадь кристалла была минимальной при заданных технологических ограничениях (4)-(6).
Конструкторско-технологические ограничения [6]:
1. Ребра всех прямоугольников параллельны осям координат;
2. Каждый прямоугольник не пересекается с любым другим прямоугольником;
3. Каждый прямоугольник не пересекается с осями координат;
4.Соединения не должны пересекаться и накладываться друг на друга;
5. Допустимое расстояние между проводниками: 3-4 мкм;
6. Минимально допустимая длина проводника 4 мкм.
3. Планирование
Под планированием понимается разбиение чипа на n прямоугольников (комнат), каждая из которых содержит по одному модулю. Совокупность комнат, полученных при разбиении, назовем планом (floorplan) (план не включает размещаемые модули).
Задачей планирования является получение такого размещения модулей, при котором площадь полученного чипа была бы минимальна. В данной работе эта задача решена с помощью метода локального спуска [11].
3.1. Q-последовательность
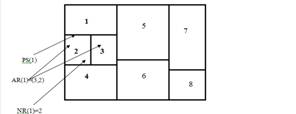
QS [11] представляет из себя последовательность, состоящую из набора индексов комнат плана и позиционных символов (Positional Symbols - R и B), описывающих расположение комнаты относительно других комнат. На рис. 1 представлен план.
|
Рис. 1. План с n=8 комнатами |
Кодирование Q-последовательности Q из плана P осуществляется по алгоритму, описанному в [11]:
Рассмотрим пример формирования QS по заданному плану (рис. 1):
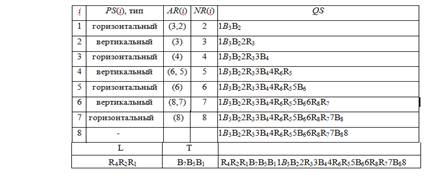
3.2. QS-декодер
Декодер - специализированная процедура, осуществляющая получение упаковки на основе исходных данных задачи и закодированного представления решения.
Для декодирования Q-последовательности Q в план P используется алгоритм, представленный в [11]:
Рассмотрим пример получения плана, из заданной QS:
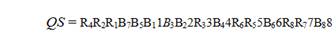
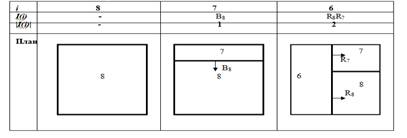
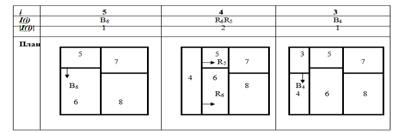
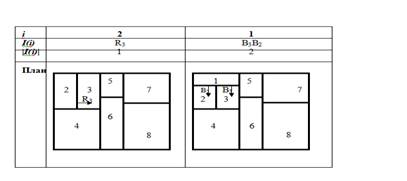
Задача планирования решена с помощью метода локального спуска [11].
3.3 Структурная схема метода локального спуска

3.4. Численные эксперименты
Таблица 1. Результаты численных экспериментов
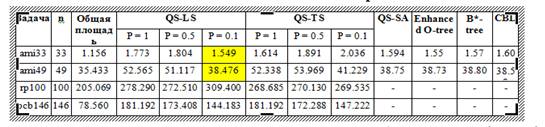
Как видно из результатов тестов (таблица 1), при размерности n=33, n=49 и P=0,1 алгоритм QS-LS показывает лучшие результаты.
4. Общая схема алгоритма для решения задачи трассировки на кристалле
Вход: план P с размещёнными по «комнатам» модулями (прямоугольниками), полученный на базе алгоритма локального спуска; структурная схема соединений модулей в виде графа, заданного списком смежности.
Выход: план P', удовлетворяющий ограничениям (1-6) с соединенными проводниками модулями в соответствии со структурной схемой.
Шаг 1. Соединение модулей плана проводниками в соответствии со структурной схемой.
Шаг 2. Построение графа G = (V,E), соответствующего схеме, в котором вершины V - это модули, а ребра E - проводники, соединяющие модули.
Шаг 3. Если имеются пересечения проводников, то применяем алгоритм проверки планарности графа на базе процедур генетического алгоритма [1], который строит базис циклов Bp и формирует приоритетный список ребер.
Шаг 4. Выполняем процедуру «декодер», осуществляющую размещение модулей по полученному приоритетному списку и их соединение с учётом условий 1-6.
Шаг 5. Конец алгоритма трассировки.
Пример работы алгоритма (шаг 1 - шаг 3) приведен в [7].
Рассмотрим подробнее шаг 4 на примере работы алгоритма декодера.
4.1. Пример работы алгоритма декодера
Шаг 1. Формирование плана размещения (рис. 2).
PL9 ={1(1,2), 6(2,3), 2(3,1); 5(1,8), 7(8,2); 8(3,6), 4(6,1); 13(6,5), 3(5,1); 15(5,8); 9(8,3); 16(6,7), 14(7,5); 10(6,4), 11(4,7); 12(8,4)}

Рис. 2. Формирование плана размещения
Шаг 2. Размещение модулей по комнатам плана.
Шаг 3. Соединение модулей (рис. 4) согласно структурной схеме (рис. 3).
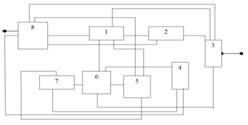
Рис. 3. Структурная схема
Расчет точек соединения производится с учетом условий 1-6 (стр. 3), т.е. соединения должны быть ортогональны, удовлетворять технологическим ограничениям и быть минимальной длины.
PL9 ={1(1,2), 6(2,3), 2(3,1); 5(1,8), 7(8,2); 8(3,6), 4(6,1); 13(6,5), 3(5,1); 15(5,8); 9(8,3); 16(6,7), 14(7,5); 10(6,4), 11(4,7); 12(8,4)}
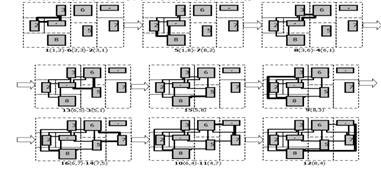
Рис. 4. Соединение модулей согласно структурной схеме (рис. 4).
Шаг 4. Упаковка полученного размещения (рис. 5).
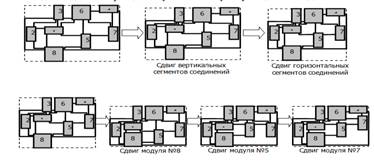
Рис. 5. Упаковка полученного размещения
Данный алгоритм был реализован на языке Delphi. Рассмотрим пример (рис. 6 - рис. 8).
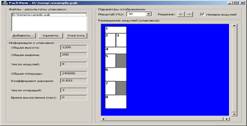
Рис. 6. План P, полученный на базе алгоритма «локального спуска» [11].
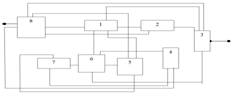
Рис. 7. Структурная схема
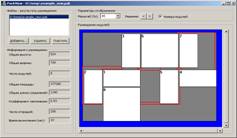
Рис. 8. План P', удовлетворяющий ограничениям 1-6, с соединенными проводниками модулями в соответствии со структурной схемой (рис. 7)
Заключение
Основные результаты работы заключаются в следующем: адаптирован метод локального спуска для решения задачи планирования, адаптирован алгоритм проверки планарности графа на базе процедур генетического алгоритма к задаче трассировки; разработан декодер, осуществляющий размещение модулей по комнатам плана и их соединение с учетом конструкторско-технологических ограничений; разработано программное обеспечение, реализующее метод локального спуска, алгоритм проверки планарности графа на базе процедур генетического алгоритма и алгоритм декодера.
Разработанный алгоритм для решения задачи проектирования СБИС позволяет, в отличие от известных подходов, легко восстановить расположение модулей на кристалле таким образом, чтобы проводники, соединяющие модули, не пересекались, с учетом конструкторско-технологических ограничений.
Рецензенты:
Юсупова Нафиса Исламовна, д.т.н., профессор, декан ФИРТ, зав. кафедрой ВМиК, ФГБОУ ВПО УГАТУ, г. Уфа.
Куликов Геннадий Григорьевич, д.т.н., профессор, зав. кафедрой АСУ, ФГБОУ ВПО УГАТУ, г. Уфа.
Библиографическая ссылка
Рихтер М.Р. РАЗРАБОТКА ДЕКОДЕРА ДЛЯ РЕШЕНИЯ ЗАДАЧИ РАЗМЕЩЕНИЯ И ТРАССИРОВКИ СБИС // Современные проблемы науки и образования. 2012. № 5. ;URL: https://science-education.ru/ru/article/view?id=7315 (дата обращения: 02.01.2026).



