В настоящее время математическое моделирование является мощным инструментом для построения адаптивных систем управления химико-технологических процессов [2]. Целью настоящей работы является реализация программно-информационной надстройки к автоматизированной системе управления технологическим процессом для обеспечения возможности прогнозирования выходных параметров (результатов проведения) процесса нормализации экстрактов «Норман-3». Возможность прогнозирования позволила реализовать систему управления, которая привнесет существенный положительный экономический эффект, при соблюдении регламентированных качественных показателей конечного продукта.
На рисунке 1 представлена схема проведения экстракционного процесса [3] нормализации экстрактов. Раствор извлеченных веществ в экстрагенте называют экстрактом, а раствор, из которого удалены экстрагируемые компоненты, - рафинатом. Исходный раствор (фаза Фx + М) и экстрагент (фаза Фу) подают в экстракционный аппарат - экстрактор, в котором происходит перенос вещества М из фазы Фх в фазу Фу. В результате получают экстракт (фаза Фу + М) и рафинат (фаза Фх). Далее проводят регенерацию экстрагента из экстракта и экстрагента из рафината. Очищенный экстрагент вновь подается на экстракцию.
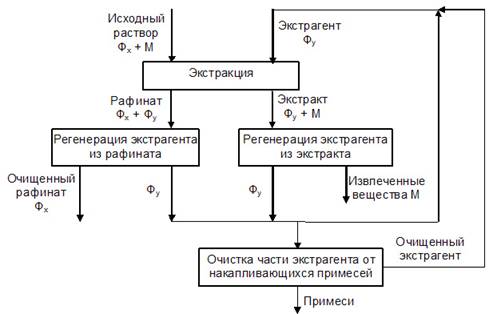
Рис. 1. Принципиальная схема получения нормализированных экстрактов «Норман-3»: Фx - фаза исходного раствора смеси экстрактов; Фу - фаза экстрагента-растворителя диметилсульфоксида (ДМСО); М - извлекаемые примеси (ФНЭТ).
Из вышеописанного технологического процесса можно сделать вывод, что наиболее важным узлом с точки зрения обеспечения регламентированного качества производимой продукции («Норман-3») является экстракционная колонна. Адаптивное управление колонной наиболее весомо скажется на качественно-экономических аспектах процесса.
Определим три группы контролируемых параметров [1], определяющие режим работы экстракционной колонны:
- расходы растворителя и очищаемого потока смеси экстрактов на вводе в колонну;
- температура растворителя и очищаемого потока смеси экстрактов на вводе в колонну;
- содержание (массовая доля) тяжелой фракции нефтяных экстрактов (ФНЭТ) в очищаемом потоке смеси экстрактов на вводе в колонну.
Значения таких параметров, как температура растворителя и очищаемого потока смеси экстрактов на вводе в колонну стабилизированы в соответствии с регламентом с использованием самостоятельных контуров регулирования. Таким образом, можно условиться, что температурные показатели проведения технологического процесса практически неизменны по времени.
В качестве основного возмущающего воздействия выступает содержание ФНЭТ в очищаемом потоке смеси экстрактов на вводе в колонну. Технологический параметр не регулируется и не может быть исключен, но оказывает прямое влияние на содержание ФНЭТ в нормализированных экстрактах «Норман-3». При завышенном содержании ФНЭТ в сырье без наличия должных контрдействий показатели конечного продукта становятся регламентационно неприемлемыми и партия забраковывается. В условиях многотоннажного производства размеры такой партии могут превышать 50 тонн, что, естественно, негативно сказывается на экономике предприятия.
С учетом малой инерциальности контура регулирования подачи расхода ДМСО, а также высокой чувствительности режима работы экстрактора при изменении подачи экстрагента видится целесообразным использование его как основное управляющее воздействие. Следует заметить, что чрезмерный расход ДМСО приводит к повышению энергоресурсов, необходимых для его регенерации, и также негативно влияет на регламентационный состав конечной продукции. Все вышеописанное формирует потребность в однозначном прогнозировании состава нормализированных экстрактов (рафината) на выходе из колонны.
Установлено, что экстракционная колонна, как объект управления, по каналу возмущения обладает большим транспортным запаздыванием, что делает невозможным использование обратной связи - напрашивается решение сложившейся проблемы путем синтеза прогнозо-компенсационной адаптивной системы управления технологическим процессом нормализации экстрактов.
Для возможности прогнозирования основного показателя качества нормализированных экстрактов (содержание ФНЭТ в очищаемом потоке на выходе из колонны) требуется составление математической модели экстрактора, которая является важнейшим элементом реализации прогнозо-компенсационной адаптивной системы управления.
Основным кинетическим уравнением массообменных процессов является уравнение массопередачи [3]:
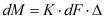 , (1)
, (1)
где dM - количество массы, переданное из одной фазы в другую, кг;
K - коэффициент массопередачи, показывающий, какое количество распределяемого вещества переходит из фазы в фазу в единицу времени через единицу поверхности контакта фаз при движущей силе, равной единице, 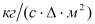 ;
;
dF - поверхность контакта фаз, м2;
Δ - движущая сила массообменного процесса.
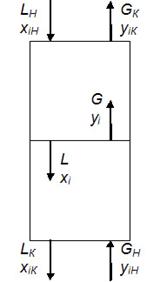
Рис. 2. К составлению материального баланса при непрерывном контакте фаз в условиях противотока: L - расход очищаемого потока (кг/ч); G - расход растворителя (кг/ч); x - концентрация экстрагируемого компонента (примесей) в очищаемом потоке;
y - концентрация экстрагируемого компонента (примесей) в растворителе.
Помимо основного уравнения массопередачи, для составления математической модели потребуется уравнение материального баланса при непрерывном противотоке.
При непрерывном противотоке, наиболее часто используемом в технике (рис. 2), материальный баланс для произвольного сечения аппарата при бесконечно малом пути выражается следующими соотношениями [3]: по всему потоку 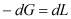 , по i-му компоненту:
, по i-му компоненту:
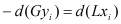 , (2)
, (2)
где L - расход очищаемого потока, кг/ч; G - расход растворителя, кг/ч; x - концентрация экстрагируемого компонента (примесей) в очищаемом потоке; y - концентрация экстрагируемого компонента (примесей) в растворителе.
Интегрирование в пределах от начальных значений входящих в это соотношение величин до их значений в произвольном сечении дает:
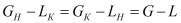 , (3)
, (3)
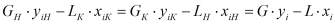 . (4)
. (4)
При малом изменении величин G и L по высоте аппарата:
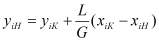 . (5)
. (5)
Уравнение массопередачи (1) для исходного раствора смеси экстрактов и потока экстрагента (растворителя):
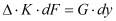 , (6)
, (6)
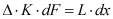 , (7)
, (7)
Процесс массопереноса протекает самопроизвольно при наличии разности между рабочими и равновесными концентрациями (при данных условиях температуры и давления) - движущей силе массообменных процессов.
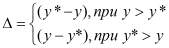 (8)
(8)
Поверхность контакта фаз зависит от высоты экстрактора [4]:
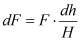 . (9)
. (9)
Учитывая выражения для движущей силы массообменного процесса (8) и поверхности контакта фаз (9), дифференциальные уравнения процесса массопередачи для каждого из потоков (6, 7) можно записать следующим образом:
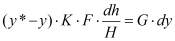 , (10)
, (10)
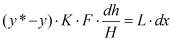 . (11)
. (11)
Введя объемный коэффициент массопередачи и дополнив дифференциальные уравнения массопередачи уравнением рабочей линии в общем виде, начальными и граничными условиями, получим математическую модель экстракционной колонны:
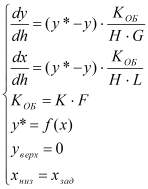 . (12)
. (12)
Оценка с использованием критерия Фишера показала адекватность математической модели.
Численной решение математической модели для определения концентрации ФНЭТ в потоках по всей высоте экстрактора представлено на рисунке 3.
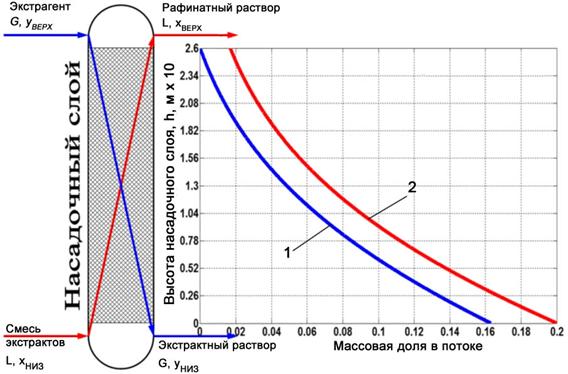
Рис. 3. Определение концентрации ФНЭТ в потоках по всей высоте колонны
с помощью математической модели при массовой доле ФНЭТ
в смеси экстрактов (исходном сырье) - 0,2.
Благодаря использованию математической модели сформировалась возможность прогнозирования концентрации ФНЭТ в рафинатном растворе на выходе из колонны, что является важнейшей частью формирования управляющего воздействия для обеспечения заданного режима работы экстрактора. Данные о массовой доле примесей в смеси экстрактов (очищаемом потоке) с промышленного рефрактометра поступают в микропроцессорный контроллер. При текущем содержании ФНЭТ в смеси экстрактов, для множества значений расхода растворителя (основное управляющее воздействие) из рабочего диапазона с помощью моделирующего алгоритма рассчитывается множество соответствующих значений содержания примесей в очищаемом потоке на выходе из колонны. Исходя из заданного режима работы при помощи математической модели, численных методов оптимизации [5] и решения дифференциальных уравнений однозначно определяется требуемое управляющее воздействие и передаётся в автономный контур регулирования расхода растворителя на вводе в колонну. По данной последовательности разработано программное обеспечение на базе программно-технического комплекса управления технологическим процессом Siemens Simatic. Программная составляющая системы управления включает два уровня (рис. 4): нижний уровень (программа микропроцессорного контроллера) и верхний уровень (исполняемый модуль среды визуализации).
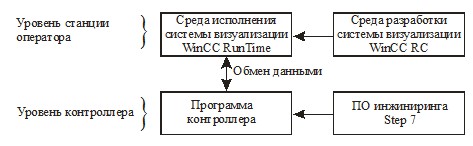
Рис. 4. Структура программного обеспечения.
Каждый уровень программного обеспечения включает среду разработки и исполняемую часть. Исполняемые части уровней контроллера и станции оператора обмениваются между собой данными.
Программное обеспечение резервированного контроллера Siemens Simatic S7-414H разрабатывается в среде программирования Step 7. Step 7 позволяет пройти последовательно все стадии, начиная от проектирования аппаратной конфигурации контроллера и написания пользовательского программного обеспечения и заканчивая программным тестом и архивацией проекта. Программа контроллера написана на языке программирования низкого S7-LAD. Представляющий собой аналог релейно-контактных схем, он служит для описания технологических задач различной сложности при высоком быстродействии.
Исполняемая часть программного обеспечения нижнего уровня имеет функционально-блочную структуру. Функциональный блок ввода аналоговых сигналов осуществляет сбор и первичную обработку информации от промышленного рефрактометра посредством аналогово-цифрового преобразователя модуля ввода.
Данные о содержании передаются по настроенному коммуникационному соединению в исполняемую среду верхнего уровня - SCADA-систему WinCC, которая является 32-битным приложением и работает в операционной системе Windows 7 на промышленных станциях оператора.
Ядро среды разработки WinCC образует нейтральная по отношению к отраслям промышленности и технологиям базовая система, которая оснащена всеми важнейшими функциями визуализации и обслуживания.
На интегрированном в среду исполнения WinCC языке Visual Basic for Application разработан макрос, выполняющий расчеты требуемого значения управляющего воздействия по запросу оператора-технолога. Далее это значение расхода экстрагента передается по коммуникационному каналу в исполняемую часть программного обеспечения контроллера в качестве задания типовому функциональному блоку регулятору. Разработанная надстройка среды визуализации в составе программного обеспечения оператора-технолога представлена на рисунке 5.
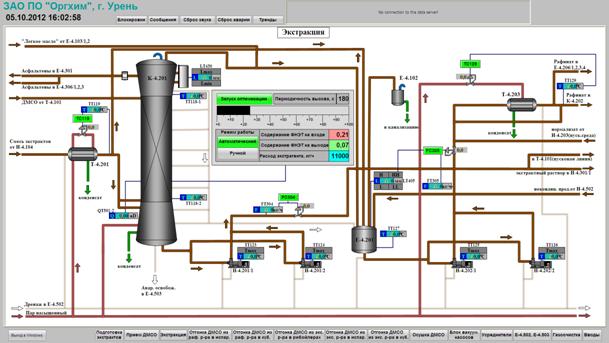
Рис. 5. Окно видеокадра расчета управляющего воздействия с использованием математической модели.
Созданный программно-технический комплекс позволил повысить эффективность производства нормализированных экстрактов «Норман-3» путем уменьшения экономических затрат при однозначном соблюдении регламентационных показателей качества.
Рецензенты
Сидягин Андрей Ананьевич, доктор технических наук, профессор, Дзержинский политехнический институт филиал Нижегородского государственного технического университета имени Р.Е. Алексеева, г. Дзержинск.
Сажин Сергей Григорьевич, доктор технических наук, профессор, академик РАЕ, генеральный директор ООО «НТЦ «АСТ», г. Дзержинск.
Библиографическая ссылка
Липин И.А., Луконин В.П. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ КАК ОСНОВА ПРОГНОЗО-КОМПЕНСАЦИОННОЙ АДАПТИВНОЙ СИСТЕМЫ УПРАВЛЕНИЯ ТЕХНОЛОГИЧЕСКИМ ПРОЦЕССОМ ЖИДКОСТНОЙ ЭКСТРАКЦИИ // Современные проблемы науки и образования. 2012. № 5. ;URL: https://science-education.ru/ru/article/view?id=7313 (дата обращения: 18.11.2025).



