Детали несоосных винтовых механизмов (НВМ) имеют несущие винтовые поверхности специального профиля, к которым предъявляются высокие требования по геометрической точности. В современном машиностроении существует группа изделий, требующих для обеспечения необходимой долговечности, значительной глубины упрочнения несущей поверхности. К таким изделиям относятся детали стрелочных переводов, крупные валы, ножи и зубья строительно-дорожных машин. Характерным примером такого рода изделий являются несоосные винтовые механизмы (НВМ), в том числе роликовые винтовые передачи (РВП) [1], к которым предъявляются высокие требования геометрической точности, контактной жесткости, усталостной прочности и долговечности.
Одной из актуальных проблем современного машиностроения является проблема повышения долговечности элементов машин по критериям прочности при одновременном снижении их металлоемкости. Непрерывное увеличение мощностей, скоростей, грузоподъемности и других параметров машин и связанный с этим рост напряженности элементов приводят к тому, что указанную проблему можно решить лишь при использовании в процессе конструирования и расчета новейших достижений науки о прочности. По мере развития методов расчета на прочность при одновременном снижении запасов прочности и материалоемкости деталей машин и конструкций традиционные инженерные расчеты по напряжениям (преимущественно номинальным) необходимо дополнять или заменять расчетами по энергетическим критериям прочности.
Известно, что расчет основных конструктивных размеров НВМ необходимо назначать исходя из расчетов деталей на нагрузочную способность, определяемую для НВМ прочностью по критериям контактной, в том числе глубинной, и изгибной выносливости, износостойкости. Существующие методики расчета заимствованы из теории зубчатых передач и подшипников качения, что не позволяет учесть важные особенности контактного взаимодействия сопрягаемых деталей НВМ, имеющего фрикционный характер.
Методы расчета основных конструктивных размеров НВМ разрабатывались в работах Д. В. Бушенина, Д. Н. Решетова, Л. В. Марголина, В. В. Козырева и др. В отличие от передач винт-гайка скольжения в несоосной винтовой паре, при постоянной осевой нагрузке на винт, составляющие ее переменные зависят от характеристик трения в контакте и опорах ведомого звена. Это приводит не только к изменению нагружения опор и других элементов в механизме, но и к изменению его кинематических характеристик. Реальный контакт в несоосной винтовой паре представляет собой пятно, форма и размеры которого определяются соотношением геометрических параметров сопрягаемых резьб, характеристиками их материалов и величиной приложенной нагрузки.
Все винтовые механизмы обычно подразделяют на кинематические, используемые в малонагруженных приводах приборов и систем управления, и силовые, работающие при значительных нагрузках на ходовой винт. К кинематическим передачам винт-гайка предъявляются высокие требования по точности, а к силовым - по прочности и износостойкости.
Развитие современной техники потребовало создания таких винтовых механизмов, которые удовлетворяют всему комплексу требований, предъявляемых как к кинематическим, так и к силовым механизмам. Детали несоосных винтовых механизмов в процессе эксплуатации подвергаются нестационарному повторно-переменному нагружению и выходят из строя в результате усталостного разрушения. С целью повышения долговечности сопрягаемые детали НВМ подвергают упрочняющей обработке. Для технологического обеспечения долговечности и качества передачи необходима информация о напряженном состоянии деталей, формирующемся в процессе эксплуатации НВМ.
Благодаря высокой жесткости и грузоподъемности НВМ находят применение в станках, измерительных машинах и промышленных роботах, все большее распространение получают в горной промышленности, воздушном и космическом транспорте, военной технике, что объясняется малой массой и нечувствительностью к обледенению и загрязнению винтовых поверхностей. Несоосные передачи являются дальнейшим развитием передач винт-гайка и в то же время наиболее общим видом винтовых механизмов, предназначенных для преобразования вращательного движения в поступательное, включающим в себя большое число как схемных, так и конструктивных разновидностей [1]. В то же время они построены на базе двух основных конструктивных решений - внутреннего сопряжения винта с резьбой кольцевой гайки или внешнего сопротивления с резьбой одного или нескольких роликов.
Отличительной особенностью несоосных винтовых механизмов, по сравнению с другими типами винтовых механизмов, является фрикционных характер передачи движения. Детали НВМ в процессе эксплуатации подвергаются нестационарному повторно-переменному нагружению и выходят из строя в результате усталостного или контактно-усталостного разрушения.
Расчет и методика определения экстремальных напряжений
Данная работа посвящена комплексному решению задачи по определению экстремальных и расчетных напряжений в любой точке детали НВМ при эксплуатации [2].
Напряженное состояние ходового винта формируется в результате взаимодействия сопрягаемых поверхностей винта и гайки (для простого НВМ) или винта и роликов (для РВП). В связи с фрикционным характером передачи движения, при рассмотрении силового взаимодействия контактирующих поверхностей необходимо учитывать суммарное влияние сил давления и трения [3].
Целесообразно при определении экстремальных напряжений выделить внутри детали три области:
- первая ограничена внутренним диаметром резьбы;
- вторая заключена между внутренним диаметром резьбы и диаметром приложения нагрузки;
- третья расположена между диаметром приложения нагрузки и наружным диаметром резьбы.
В каждой области результирующие напряжения являются некоторой суммой нормальных и касательных напряжений от всех рассматриваемых видов деформаций (деформаций тела винта, витка и контактных деформаций). Зная нормальные и касательные составляющие напряжений по граням элементарного объема, легко определить экстремальные и расчетные напряжения для любой точки вышерассмотренных областей.
При расчете напряженного состояния в большинстве случаев решается плоская задача, не позволяющая учесть пространственную геометрию сопрягаемых профилей. Во всех случаях принимается во внимании только одна точка контакта, хотя заранее известно, что нагрузка в НВМ распределена по многочисленным точкам контакта, имеющим взаимное пространственное угловое и линейное относительное смещение. Вследствие фрикционного характера передачи движения в НВМ недопустимо пренебрежение силами трения в контакте сопрягаемых звеньев. При определении напряженного состояния в точке тела необходимо в окрестности этой точки выделить элемент объема в виде прямоугольного параллелепипеда. По граням выделенного элемента действуют составляющие напряжений в соответствующих координатных плоскостях [4].
В каждой области результирующие напряжения являются некоторой суммой нормальных и касательных напряжений от всех рассматриваемых видов деформаций (деформаций тела винта, витка и контактных деформаций). Зная нормальные и касательные составляющие напряжений по граням элементарного объема легко определить экстремальные и расчетные напряжения для любой точки вышерассмотренных областей.
Задача определения напряженного состояния сводится к расчету главных (экстремальных) напряжений от всех действующих силовых факторов в любой точке детали в произвольный момент времени [6]. Данные о значениях экстремальных напряжений в локальной области несущей детали НВМ в тот или иной момент времени являются основой расчета параметров спектра нагружения и глубины наиболее нагруженного несущего слоя. Сведения о спектре нагружения несущей поверхности дают возможность прогнозировать ее долговечность. Знание глубины несущего слоя позволяет предъявить научно обоснованные требования к величине, знаку и градиенту изменения технологических остаточных напряжений. Это создает предпосылки выбора рационального технологического маршрута и режимов обработки несущей поверхности [2].
При расчете деталей несоосных винтовых механизмов наибольший интерес вызывает напряженное состояние наиболее ответственной детали передачи - ходового винта. В случае равномерного распределения рабочей нагрузки между роликами передачи поля напряжений, сформированные в винте под действием сил от каждого из роликов, компенсируют друг друга, а величины главных напряжений зависят только от величины осевой составляющей нагрузки Fa и диаметра винта d. Однако в реальной передаче вследствие погрешностей сборки и изготовления отдельных звеньев нагрузка между роликами распределяется неравномерно. В работе предпринята попытка оценить степень влияния неравномерности распределения нагрузки по роликам в РВП на величину главных напряжений в ходовом винте.
При расчете главных напряжений ходовой винт допустимо моделировать брусом круглого сечения с закрепленными в опорах концами. Известно, что подавляющая доля нагрузки воспринимается первыми витками резьбы, находящимися в контакте с сопрягаемой деталью. Так как расстояние между соседними витками резьбы винта, воспринимающими нагрузку, составляет 0,4...2,5 мм, что много меньше длины винта, силы, действующие на виток резьбы, считаются лежащими в одном поперечном сечении. Таким образом, при проведении расчетов вся нагрузка считается сосредоточенной в одном поперечном сечении, отстоящем на расстоянии z (переменная величина) от левого торца винта. Рассматривается плоское напряженное состояние винта. Определяются главные напряжения, формирующиеся в результате взаимодействия полей напряжений изгиба, кручения, растяжения, сжатия и сдвига.
Расчет главных напряжений невозможен без предварительного силового расчета. В связи с фрикционным характером передачи движения в РВП, при рассмотрении силового взаимодействия контактирующих поверхностей необходимо учитывать суммарное влияние сил давления и трения. В несоосной винтовой паре при постоянной осевой нагрузке на винт составляющие ее переменны. Радиальная Fr и тангенциальная Ft составляющие нагрузки могут быть выражены через осевую Fa составляющую векторной суммы сил давления и трения: 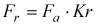 ,
, 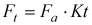 . Проведенные исследования показали, что Kr и Kt принимают значения в диапазонах:
. Проведенные исследования показали, что Kr и Kt принимают значения в диапазонах: 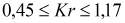 ;
; 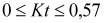 , причем наибольшим значениям Kr соответствуют средние и малые значения Kt, а наибольшим Kt - средние и малые Kr [3.7]. Наибольшая величина главных напряжений соответствует максимальным значениям Kr и Kt, поэтому для расчетов целесообразно принять
, причем наибольшим значениям Kr соответствуют средние и малые значения Kt, а наибольшим Kt - средние и малые Kr [3.7]. Наибольшая величина главных напряжений соответствует максимальным значениям Kr и Kt, поэтому для расчетов целесообразно принять 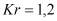 и
и 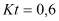 .
.
Исходя из вышеизложенного, для определения экстремальных значений напряжений на поверхности и на глубине винта несоосного винтового механизма с целью облегчения расчетов может быть предложена инженерная формула вида:
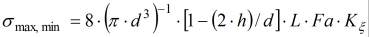
где 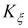 - коэффициент, характеризующий неравномерность распределения нагрузки по роликам в РВП.
- коэффициент, характеризующий неравномерность распределения нагрузки по роликам в РВП.
Необходимость экспериментального определения деформаций и напряжений в деталях машин возникает при проверке точности выполнения расчетов. Для измерения деформаций применяются различные методы и приборы в зависимости от задач исследования [7].
Экспериментальное определение напряжений
Наиболее распространенный метод экспериментального исследования распределения деформаций заключается в измерении деформаций на поверхности детали с помощью механических, оптических или электрических тензометров. Большим преимуществом электрических тензометров, среди которых наибольшее распространение получили проволочные датчики сопротивления, является возможность измерения с их помощью динамических деформаций и деформаций в труднодоступных точках деталей. По замеренным деформациям можно рассчитывать и величины напряжений в соответствующих точках.
Экспериментальное определение напряжений в теле винта проводили на машине типа ДМЗОМ [4]. Для проведения исследований датчики подключались к регистрирующему устройству, в качестве которого использовался цифровой омметр. Для более точного определения напряжений нагрузку прикладывали ступенями через 50 Н. При этом фиксировали по прибору значения сопротивления датчиков R. Использовались проволочные датчики из тонкой константановой проволоки диаметром 0,02 мм, с базой 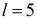 мм. Проволочный датчик наклеивался на исследуемую деталь и деформировался вместе с ней [8].
мм. Проволочный датчик наклеивался на исследуемую деталь и деформировался вместе с ней [8].
Для определения деформаций в данном экспериментальном исследовании применяется стандартная прямоугольная розетка датчиков, состоящая из трех одинаковых датчиков, наклеенных под разными углами к оси винта. Для перехода от компонент тензора деформаций, полученных с помощью этих розеток, к соответствующим компонентам напряженного состояния в упругой области воспользовались законом Гука.
Испытанию подвергались образцы, которые имитировали ходовой винт НВМ. Проведена серия испытаний образцов для определения напряжений в конкретных точках детали.
Заключение
В результате аналитического решения задачи методами сопротивления материалов получены выражения для определения главных напряжений в любой точке винта. Установлена степень влияния неравномерности распределения нагрузки по роликам, погрешности положения роликов, конструктивных параметров винта на величину главных напряжений. Предложена инженерная формула для расчета максимальных напряжений, возникающих в теле винта при эксплуатации [5].
Предлагаемые зависимости при знании закона изменения во времени координат точки приложения нагрузки позволяют оценить динамику изменения экстремальных напряжений в процессе эксплуатации, определить параметры спектра нагружения, произвести расчет винта на долговечность. Разработана также обобщенная математическая модель напряженного состояния сопрягаемых деталей НВМ, охватывающая все известные способы закрепления многоступенчатых деталей НВМ.
Полученные незначительные расхождения между экспериментальными и теоретическими значениями главных и расчетных напряжений на поверхности винта позволяют считать разработанную автором методику достаточно точной и рекомендовать ее для расчета напряженного состояния ходовых винтов.
Рецензенты:
Жизняков А. Л., д.т.н., профессор, первый заместитель директора МИ ВлГУ, Муромский институт (филиал) ФГБОУ ВПО «Владимирский государственный имени Александра Григорьевича и Николая Григорьевича Столетовых, г. Муром.
Лазуткин А. Г., д.т.н., профессор, Муромский институт (филиал) ФГБОУ ВПО «Владимирский государственный имени Александра Григорьевича и Николая Григорьевича Столетовых», г. Муром.
Библиографическая ссылка
Лодыгина Н.Д. ВЛИЯНИЕ НЕРАВНОМЕРНОСТИ РАСПРЕДЕЛЕНИЯ НАГРУЗКИ НА ВЕЛИЧИНУ ЭКСТРЕМАЛЬНЫХ НАПРЯЖЕНИЙ В СЕЧЕНИЯХ ДЕТАЛЕЙ ВИНТОВЫХ МЕХАНИЗМОВ // Современные проблемы науки и образования. 2012. № 5. ;URL: https://science-education.ru/ru/article/view?id=7295 (дата обращения: 16.02.2026).



