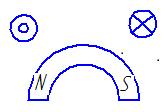
Известные конструкции ЭМПЭ колебательного движения [1; 5] представляют собой ЭМПЭ, воспринимающие колебания только в одном направлении, что приводит к потерям полезной механической энергии от колебаний в других направлениях, а, следовательно, является причиной низкого КПД. Кроме того, однонаправленность воспринимаемых ЭМПЭ колебаний ограничивает их применение на практике узкоспециальными техническими устройствами. Для устранения данных недостатков авторами предлагается оригинальное техническое решение [2] трехкоординатного колебательного ЭМПЭ (ТКЭП) (рис. 1).
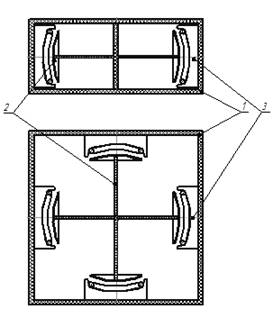
Рис. 1. Конструкция предлагаемого ТКЭП.
Предложенное техническое решение содержит корпус 1, на котором закреплена подвижная часть 2, представляющая собой постоянные магниты, намагниченные в радиальном направлении, жестко закрепленные на упругих стержнях, выполненные, например, из пружинной стали. По периметру корпуса 1 расположены катушки 3.
Постоянные магниты на упругих стержнях представляют собой механическую колебательную систему с малым трением. При этом жесткость стержней достаточна, чтобы не допустить «провисания» постоянных магнитов относительно катушек. При возникновении внешних возмущений любого направления (например, удар, толчок, вибрации), происходит отклонение постоянных магнитов от точки равновесия, т.е. в механической системе возникают свободные или вынужденные колебания, направление и амплитуда которых зависит от внешнего возмущающего воздействия. В катушках наводится ЭДС, которая через выпрямитель заряжает конденсатор (на рисунке не показан), обеспечивающий питание электрической схемы.
Таким образом, предложенное техническое решение позволяет увеличить КПД ЭМПЭ колебательного движения в 2-3 раза.
В связи с изложенными выше преимуществами предлагаемой конструкции актуальной научно технической задачей и целью работы является разработка математического описания и практических рекомендаций конструктивного исполнения ТКЭП.
Для выполнения поставленной цели решены следующие задачи:
- разработана математическая модель, отражающаая взаимосвязанную зависимость между электрическими, магнитными и механическими параметрами оригинальной конструкции ТКЭП;
- определены конструкции ТКЭП с наибольшим значением магнитной индукции в воздушном зазоре;
- определены конструкции ТКЭП с наибольшей величиной вырабатываемой ЭДС.
Разработка математической модели, отражающей взаимосвязанную зависимость между электрическими, магнитными и механическими параметрами оригинальной конструкции ТКЭП, осуществлялась по расчетной схеме, содержащей колебательный контур со сферическим постоянным магнитом и кольцевой обмоткой, рисунок 2.
Ввиду сложности расчетов используются стандартные для данного типа задач допущения:
- возмущающие воздействия имеют импульсный характер, т.е. колебания в колебательном контуре затухающие;
- магнитная проницаемость немагнитного рабочего зазора ЭМПЭ равна проницаемости вакуума μ0, магнитная проницаемость постоянных магнитов 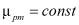 ;
;
- потоки рассеяния не учитываются;
- предполагается, что постоянный магнит при колебаниях не выходит за пределы обмотки;
- тангенциальная составляющая магнитного поля не учитывается ввиду того, что она практически не участвует в преобразовании механической энергии в электрическую.
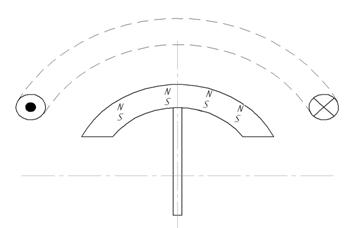
Рис. 2. Расчетная схема ЭМПЭ.
Координата α крутильных затухающих колебаний [4] постоянного магнита принимается в виде:
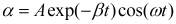 , (1)
, (1)
где 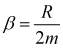 - коэффициент затухания; R - коэффициент, характеризующий силу сопротивления, которая принимается в виде
- коэффициент затухания; R - коэффициент, характеризующий силу сопротивления, которая принимается в виде 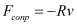 ;
; 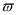 - угловая скорость постоянного магнита; A - амплитуда колебаний.
- угловая скорость постоянного магнита; A - амплитуда колебаний.
Угловая скорость:
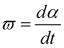 , (2)
, (2)
Дифференцирование (2) с учетом (1), определяет выражение угловой скорости подвижного элемента:
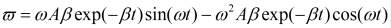 . (3)
. (3)
Отношение линейной скорости к угловой:
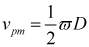 . (4)
. (4)
ЭДС ТКЭП определяется по известной формуле:
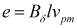 . (5)
. (5)
С учетом того, что катушка рассматриваемой конструкции имеет кольцевую форму, тогда:
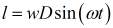 , (6)
, (6)
где D - диаметр кольцевой обмотки; w - число витков обмотки.
С учетом (6):
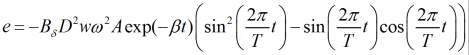 . (7)
. (7)
Период затухающих колебаний:
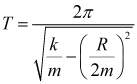 , (8)
, (8)
где k - коэффициент жесткости стержня.
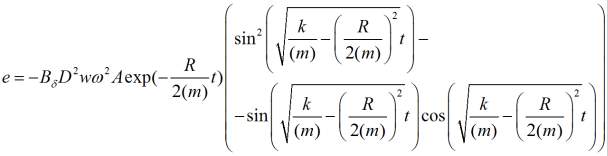 (9)
(9)
Так как при движении постоянного магнита индукция в зазоре ТКЭП не постоянна, то важно определить ее усредненое значение.
Радиальная составляющая напряженности магнитного поля сферического постоянного магнита [3] принимается в виде:
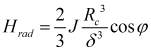 , (10)
, (10)
где 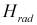 - радиальная составляющая напряженности магнитного поля;
- радиальная составляющая напряженности магнитного поля; 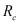 - радиус сферы;
- радиус сферы; 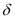 - воздушный зазор.
- воздушный зазор.
С учетом того, что:
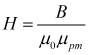 , (11)
, (11)
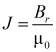 . (12)
. (12)
Тангенциальная и радиальная составляющие магнитной индукции
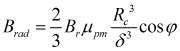 , (14)
, (14)
Для определения среднего значения магнитной индукции в воздушном зазоре угол φ представляется в виде:
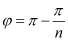 , (15)
, (15)
где n - количество членов ряда:
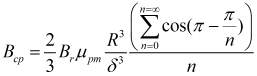 . (16)
. (16)
Выражение (9) с учетом выражения (18) является математической моделью ТКЭП, отражающей взаимосвязь механических, магнитных и электрических параметров.
Основной задачей ТКЭП является выработка максимальной электрической энергии, на что, как показано в выражении (9), влияет непосредственно значение магнитной индукции в воздушном зазоре. Индукция в воздушном зазоре определяется непосредственно величиной воздушного зазора, конструкцией магнитной системы (МС) и активными материалами.
Величина воздушного зазора ограничивается жесткостью упругого стержня и должна быть минимизирована с учетом данного параметра. Применение более энергоемких материалов может привести к удорожанию конструкции, что нецелесообразно. Таким образом, наиболее эффективным методом оптимизации ТКЭП по величине магнитной индукции является оптимизация МС ТКЭП.
Задача оптимизация МС осуществлялась методом сравнительного анализа ряда конструкций по критерию магнитной индукции в воздушном зазоре с учетом нелинейности характеристик материалов и по критерию ЭДС с учетом изменения массы МС. Ряд сравниваемых конструкций представлен в таблице 1.
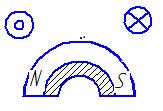
Таблица 1 - Типы конструктивных исполнений МС ТКЭП
|
№ варианта |
Тип конструктивного исполнения |
Описание |
|
1 |
|
Активная система с постоянными магнитами |
|
2 |
|
Активная система с постоянными магнитами и ферромагнитной накладкой, расположенной под магнитом |
|
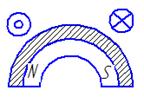
3 |
|
Активная система с постоянными магнитами и ферромагнитной накладкой, расположенной над магнитом |
|
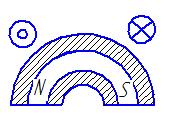
4 |
|
Активная система с постоянными магнитами и ферромагнитной накладкой, расположенной под и над магнитом |
Расчет значений магнитной индукции производился методами компьютерного моделирования в программном комплексе Ansys.
При моделировании принимались заданными геометрические размеры МС: радиус постоянного магнита 30 мм, воздушный зазор 1 мм, толщина постоянного магнита 10 мм, толщина ферромагнитной накладки 3 мм. В качестве материала постоянных магнитов принимался сплав редкоземельных металлов NdFeB с остаточной индукцией 1,13 Тл и радиальным направлением намагниченности, в качестве материала ферромагнитной накладки принимался ферромагнетик с постоянной магнитной проницаемостью 10 000.
В результате моделирования были получены значения магнитной индукции в воздушном зазоре для исследуемых конструктивных вариантов, которые были сведены в диаграмму (рис. 3).
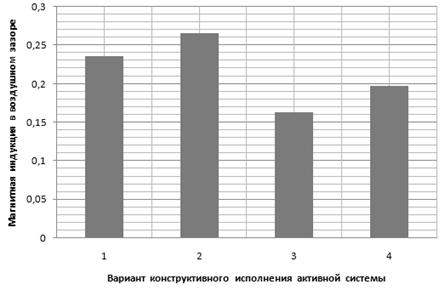
Рис. 3. Диаграмма распределения магнитной индукции для различных конструктивных вариантов.
Анализ диаграммы (рис. 3) показал, что наибольшим значением магнитной индукции обладает конструктивный вариант с ферромагнитной накладкой, расположенной под магнитом, а наименьшей - с ферромагнитной накладкой, расположенной над магнитом.
Оптимизации МСТКЭМ по критерию ЭДС производилась на основе данных, полученных при решении предыдущих вариантов. Из выражения (8) видно, что помимо магнитной индукции ЭДС зависит от массы МС.
При оценке величины ЭДС производились численные расчеты по выражению (8) с учетом данных компьютерного моделирования в программной среде Matchcad. При этом при расчетах варьируемыми параметрами были изменения магнитной индукции и изменения массы, прочие параметры принимались постоянными. Результаты расчетов представлены в виде диаграммы (рис. 4).
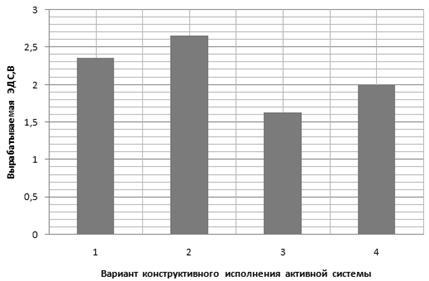
Рис. 4. Диаграмма вырабатываемой ЭДС для различных МС.
Анализ диаграммы (рис. 4), показал, что наибольшим значением вырабатываемой ЭДС обладает конструктивный вариант с ферромагнитной накладкой, расположенной под магнитом, а наименьшей - с ферромагнитной накладкой, расположенной над магнитом.
Для анализа области применения разработанной математической модели производилась оценка ее точности в зависимости от количества членов ряда.
Результаты расчета среднего значения магнитной индукции от количества элементов ряда представлены в таблице 2.
Таблица 2 - Численные расчеты среднего значения магнитной индукции
|
Количество членов ряда |
Значение средней магнитной индукции |
|
10 |
0,48393148 |
|
50 |
0,49176087 |
|
100 |
0,4916 |
|
500 |
0,490688 |
|
1000 |
0,49075 |
|
5000 |
0,490827 |
Анализ данных, таблица 2, показал, что при количестве членов ряда более 100 расхождение расчетов составляет 10-3, более 500 расхождение составляет 10-4.
Полученные значения расхождения позволяют использовать разработанную математическую модель на практике.
Выводы
- Предложена оригинальная конструкция электромеханического преобразователя с тремя степенями свободы подвижного элемента и обоснована перспективность ее применения на практике
- Разработана математическая модель электромеханического преобразователя с тремя степенями свободы подвижного элемента, отражающая взаимосвязанную зависимость между электрическими, магнитными и механическими параметрами.
- Анализ численных расчетов по разработанной математической модели показал, что расхождение при количестве членов ряда более 500 составляет не более .
- Произведена оптимизация магнитной системы электромеханического преобразователя с тремя степенями свободы подвижного элемента методами компьютерного моделирования.
- Установлено в результате оптимизации, что наибольшим значением вырабатываемой ЭДС и магнитной индукцией в воздушном зазоре обладает конструктивный вариант с ферромагнитной накладкой, расположенной под магнитом, а наименьшей - с ферромагнитной накладкой, расположенной над магнитом.
Рецензенты
Ураксеев М.А., д.т.н., профессор кафедры ИИТ ФГБОУ ВПО «УГАТУ», г. Уфа.
Гизатуллин Ф.А., д.т.н., профессор кафедры ЭМ ФГБОУ ВПО «УГАТУ», г. Уфа.
Библиографическая ссылка
Хайруллин И.Х., Риянов Л.Н., Вавилов В.Е. ТРЕХКООРДИНАТНЫЙ КОЛЕБАТЕЛЬНЫЙ ЭЛЕКТРОМЕХАНИЧЕСКИЙ ПРЕОБРАЗОВАТЕЛЬ ЭНЕРГИИ // Современные проблемы науки и образования. 2012. № 5. ;URL: https://science-education.ru/ru/article/view?id=7245 (дата обращения: 16.02.2026).