Основным количественным показателем, используемым при локальной оценке и прогнозе устойчивости склонов, является коэффициент устойчивости (коэффициент запаса устойчивости), представляющий собой отношение сумм удерживающих и сдвигающих сил, действующих по поверхности предполагаемого смещения оползневого тела (при круглоцилиндрической поверхности смещения отношение сил заменяется отношением моментов тех же сил)[1,2].
Для определения значений удерживающих и сдвигающих сил используются параметры грунта а именно j - угол внутреннего трения и С - общее сцепление грунта. Значение параметров j и C определяют в «срезных приборах» для чего берут образец грунта, прикладывают к нему горизонтальную и вертикальную нагрузки, и изменяя ее фиксируют значения нагрузки при которой произошел срез. Причем параметры j и C определяют только для горизонтальной плоскости среза, то есть, считают параметры грунта изотропными [3].
В то же время при исследовании пород г. Ульяновска И.С. Рогозин делает замечание «...в природной обстановке глины сплошь трещиноваты и разбиты на многогранники разных размеров и формы. В шурфах, врезанных в коренные несмещенные и невыветрелые глины, можно было видеть, что все трещины обычно плотно сомкнуты и ориентированы различно, преобладающее направление - южное. Горизонтальных трещин нет совершенно, но есть вертикальные ...»[4]. Это в свою очередь подразумевает, что параметры глин в естественных склонах могут являться анизотропными, и соответственно значения φ и C различны для разных углов среза грунта.
Проведем синтез математической анизотропной модели грунта для применения ее в расчете устойчивости склона в методе круглоцилиндрической поверхности.
Закон, описывающий сопротивление глинистых грунтов сдвигу можно записать в следующем виде:
Spw=P x tg φw+Σw+Сc (1)
или
Spw=P x tg φw +Сw (2)
где: Spw - сопротивление глинистого грунта сдвигу при данной нагрузке P и влажности w; P - действующее нормальное напряжение;φw- угол внутреннего трения грунта с влажностью w; Cw - общее сцепление грунта; Сс - структурное сцепление; Σw - сцепление связанности грунта с влажностью w.
На основании вышесказанного формула (2) может быть записана в виде:
Spwi=P x tg φwi +Сwi (3)
где: φwi - общее значение угла внутреннего трения при угле среза (i) равном углу между горизонталью и нормалью к зеркалу среза; Сwi - общее сцепление при угле среза (i) равном углу между горизонталью и нормалью к зеркалу среза.
Будем искать значения параметров φw и Cw для произвольной плоскости среза как функцию от значений в горизонтальной и вертикальной плоскости в виде
X(i)=X^ x f(i) +X_ f `(i) (4)
где: i - угол между горизонталью и нормалью к зеркалу среза; X^ - значение параметра при i=90° (вертикальный срез); X_ - значение параметра при i=0° (горизонтальный срез); f(i) и f `(i) некоторые неизвестные коэффициенты зависимые от i.
Сразу можно определить некоторые характерные значения f(i) и f `(i):
- 1. при i=90°, X= X^, то есть f(90°) = 1 а f `(90°)=0;
- 2. при i=0°, X= X_, то есть f(0°) = 0 а f `(0°)=1;
- 3. при i=45°, X^= X_ то есть f(45°) = 0,5 а f `(45°)=0,5;
- 4. физический смысл имеют коэффициенты f(i) и f `(i), при которых значение параметров Xi при любом i лежит в границах значений X^ и X_;
- 5. значения коэффициентов должны быть зеркально симметричными относительно значений при 45°.
Для определения коэффициентов f(i) и f `(i) проведем серию сдвиговых испытаний. На рис. 1 ... 6 представлены полученные данные.
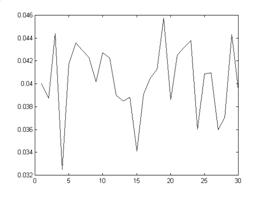
Номер образца
Рис. 1. График значений предельной горизонтальной нагрузки для вертикальной плоскости среза при вертикальной нагрузке 0,1 МПа. Мат. ожидание 0,0404МПа, среднеквадратичное отклонение 9% относительно мат. ожидания
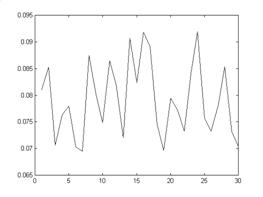
Номер образца
Рис. 2. График значений предельной горизонтальной нагрузки для вертикальной плоскости среза при вертикальной нагрузке 0,2 МПа. Мат. ожидание 0,0791 МПа, среднеквадратичное отклонение 8,7% относительно мат. ожидания
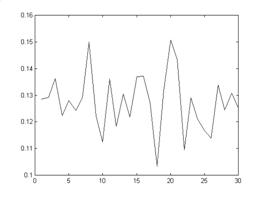
Номер образца
Рис. 3. График значений предельной горизонтальной нагрузки для вертикальной плоскости среза при вертикальной нагрузке 0,3 МПа. Мат. ожидание 0,1275 МПа, среднеквадратичное отклонение 8,4% относительно мат. ожидания
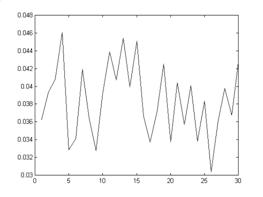
Номер образца
Рис. 4. График значений предельной горизонтальной нагрузки для горизонтальной плоскости среза при вертикальной нагрузке 0,1 МПа. Мат. ожидание 0,0384 МПа, среднеквадратичное отклонение 10,7% относительно мат. ожидания
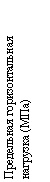
Номер образца
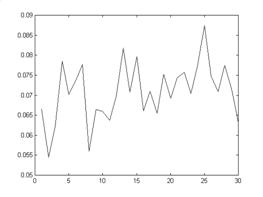
Рис. 5. График значений предельной горизонтальной нагрузки для горизонтальной плоскости среза при вертикальной нагрузке 0,2 МПа. Мат. ожидание 0,0709 МПа, среднеквадратичное отклонение 10% относительно мат. ожидания
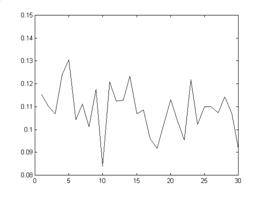
Номер образца
Рис. 6. График значений предельной горизонтальной нагрузки для горизонтальной плоскости среза при вертикальной нагрузке 0,3 МПа. Мат. ожидание 0,1086, среднеквадратичное отклонение 9,45% относительно мат. ожидания
На рис. 7 показан график зависимости предельной горизонтальной нагрузки от вертикальной нагрузки для горизонтальной и вертикальной ориентации плоскости среза (среднее значение).
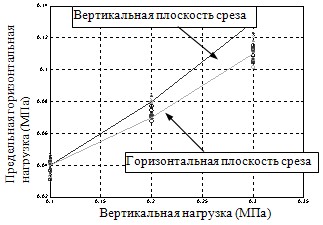
Рис. 7. График зависимости значений предельной горизонтальной нагрузки от вертикальной нагрузки для горизонтальной и вертикальной ориентации плоскости среза (среднее значение)
По графику получаем, что при вертикальной ориентации плоскости среза угол внутреннего трения равен 27°, сцепление грунта 0,1 кПа; при горизонтальной ориентации плоскости среза угол внутреннего трения равен 21°, сцепление грунта 4,8 кПа - параметры грунта анизотропные.
Чтобы определить зависимость значений параметр j и С от угла среза нормируем их, и построим график зависимости параметров от угла среза для серии измерений рис. 8. Для нормировки будем делить значение параметра при данном угле на значение параметра при угле среза 0° при нормировании угла внутреннего трения и на значение параметра при угле среза 180° при нормировании сцепления грунта (максимальные значения параметров).
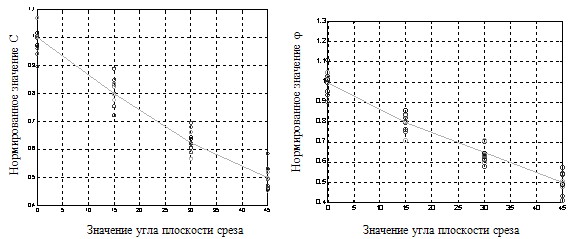
Рис. 8. График значений параметров С и j при плоскостях среза равных 15°, 30°, 45° к горизонтали.
Из графика видно, что зависимость является линейной и значения f(i) и f `(i) можно представить в виде: f(i)= i/90 , f `(i)= (90° - i)/90. Для углов среза i больше 90° необходимо рассчитывать f(i) и f `(i) как для угла 180° - i.
Зависимость параметров грунта срезанного по произвольной плоскости можно записать следующим образом:
![]() (5)
(5)
СПИСОК ЛИТЕРАТУРЫ:
- 1. Теоретические основы инженерной геологии /под ред.
Сергеева Е.М. М.: Недра, 1986.- 250 с. - 2. Тер-Степанян Г.И. и др. Ползучесть грунтов и склонов //Проблемы геомеханики. - Ереван: Изд-во АН Арм. ССР, 1985.-67с.
- 3. Современные методы прогноза оползневого процесса / Под ред. М.В. Чуринова, Е.П. Емельяновой и Г.Р. Хоситашвили. - М.: Наука, 1981. 120 с.
- 4. И.С. Рогозин «Оползни Ульяновска и опыт борьбы с ними» М. Издателство «Академии наука» СССР 1961г. - 75 с.
Библиографическая ссылка
Бобрович А.С. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ГРУНТА, УЧИТЫВАЮЩАЯ АНИЗОТРОПНОСТЬ ЕГО ПАРАМЕТРОВ В ПРИРОДНОЙ ОБСТАНОВКЕ // Современные проблемы науки и образования. 2007. № 6-1. ;URL: https://science-education.ru/ru/article/view?id=723 (дата обращения: 20.02.2026).



