Деятельность системы здравоохранения зависит от многих факторов, которые трудно предсказать и измерить. Неопределенность действия системы здравоохранения является ее очень важным параметром, и поэтому без соответствующего информационного обеспечения не может существовать система управления медицинской помощью. Целью сбора информации является получение знаний, необходимых для выработки управленческих решений, направленных на совершенствование организации лечебного процесса. Источниками информации могут быть документы: внутренние - это чаще всего медицинская документация лечебно-профилактического учреждения, так и внешние - изменения в законодательной системе, в социальной и экономической сферах и т.д.
В настоящее время медицинскими учреждениями широко применяются разнообразные информационные системы, которые могут служить для решения следующих задач:
- создания единого информационного пространства для ускорения доступа к информации, повышения качества медицинской документации;
- мониторинга и оперативного управления процессом оказания медицинской помощи для снижения вероятности врачебной ошибки;
- повышения прозрачности деятельности медицинского учреждения и эффективности принимаемых управленческих решений;
- анализа экономических аспектов оказания медицинской помощи;
- обеспечение ЛПУ системы муниципального и регионального уровня здравоохранения программными средствами формирования статистической отчётности на основании обработки первичных документов;
- обеспечение накопления первичных и статистических данных на уровне ЛПУ для анализа состояния здоровья обслуживаемого населения и деятельности ЛПУ.
Как указывалось в работах [1], одним из компонентов (подсистемой) общей системы управления является система статистического контроля. Следует отметить, что идея эта не нова и заимствована из существующих промышленных систем обеспечения качества продукции. Так, например, в действующих ГОСТах 40.9001-03-87.88 [2], соответствующих международным стандартам ИСО 9001-9003-87 [3], статистический контроль является одним из важнейших средств управления качеством. Во многом это связано с тем, что большинство производственных закономерностей имеют статистическую природу.
Долгое время статистическая обработка информации была трудоемкой и сложной процедурой. Однако, с развитием компьютерной техники, даже самые сложные статистические расчеты оперативно выполняются современными программами, например, Excel MS Office, Statistica, Statgrafics, MatLab и MathCad и т.д.
Прикладные программы позволяют решить ряд важных практических задач лечебно-профилактического учреждения на основе имеющейся информации. К числу таких задач можно отнести:
- Оперативное определение среднего количества обращений за оказанием первичной медицинской помощью по определенным видам нозологии к конкретному врачу - это позволит определить границы обслуживаемых участков для рационального распределения нагрузки на врача.
- Оперативное определение среднего количества обращений за оказанием медицинской помощи второй раз в жизни по определенным нозологиям, что позволит прогнозировать принадлежность пациента к определенной группе риска.
- Оперативное определение среднего количества обращений за оказанием медицинской помощи второй раз в году, что позволит прогнозировать возможность попадания данного пациента в группы диспансерного наблюдения.
- Оперативное определение среднего количества совпадений между первичным и заключительным диагнозом, что позволит оценивать качество диагностических мероприятий.
- Оперативное определения среднего количества показателей результата лечения: выздоровление, улучшение, ухудшение, госпитализация, смерть и т.д., что позволит оценивать качество адекватности методов лечения.
- Оперативное определение показателя интенсивности нагрузки врача для выяснения средней нагрузки на врачебную должность.
- Оперативное определение показателя сложности выполненных работ как одного из характеристик деятельности врача.
- Оперативное определение показателей качества и медицинской результативности процесса оказания медицинской помощи для оценки соответствия применяемых технологий проблемам состояния здоровья пациентов.
- Принятие управленческих решений, направленных на осуществление основной задачи ЛПУ - обеспечение оказания медицинской помощи в полном объеме согласно нормативных требований, плановых заданий и минимальных затратах, на основе оценки наиболее значимых факторов.
Для решения вышеуказанных задач в качестве исходных данных используются базы данных ЛПУ. Исходные данные получают при помощи SQL-запросов, обрабатывают, применяя основные положения математической статистики.
.Первичная статистическая обработка
С точки зрения статистики все пациенты, обратившиеся за оказанием первичной медицинской помощи, представляют собой генеральную совокупность. Группа пациентов, обратившихся к некоторому врачу или на некоторый участок, образует выборку. Для корректного использования методов математической статистики выборка должна обладать свойствами репрезентативности (представительности), состоятельности, несмещенности и эффективности.
Первое свойство означает одинаковую вероятность попадания наблюдений (контрольных точек) из генеральной совокупности в выборку. Второе - близость выборочного значения к истинному значению случайной величины, третье и четвертое - отсутствие значительных расхождений в выборочных средних по сравнению с их точными теоретическими значениями, а также минимизацию средних квадратических отклонений статистических оценок показателей от их теоретических значений. Все указанные выше требования обычно называют термином «статистическая устойчивость» («статистическая управляемость») случайного явления (события, случайной величины, случайной функции).
Статистическая устойчивость случайного явления (процесса) представляет собой обязательное условие возможности применения к анализу данного явления статистических и вероятностных методов. Поэтому именно с этой задачи должна начинаться статистическая обработка информации.
Первичная статистическая обработка результатов обращений за медицинской помощью с целью проверки статистической устойчивости и управляемости должна начинаться с использования прикладных программных продуктов для получения общих статистических оценок выборочных средних и дисперсий. В упомянутых выше пакетах Statistica, Statgrafics имеются соответствующие опции (Descriptive Methods →Summary Statistics).
После ввода данных по результатам количества ежедневных обращений за оказанием первичной медицинской помощью вычисляются [4]:
1. Выборочные средние значения обращений за оказанием первичной медицинской помощью за один день, один месяц, один год и т.д. Так, если xi - количество обращений за определенный период (![]() ), а n - число периодов, то выборочная средняя статистических оценок будет равна:
), а n - число периодов, то выборочная средняя статистических оценок будет равна:
![]() , (1)
, (1)
2. Выборочная групповая средняя статистическая оценка дисперсии обращений равна:
![]() (2)
(2)
3. Размах значений в подгруппе определяется как разница между максимальным и минимальным значением:
R= Хmax-Xmin (3)
При первичной статистической обработке кроме перечисленных выше, могут быть вычислены и другие статистические характеристики процесса оказания медицинской помощи, которые позволили бы сделать вывод о том, какому закону распределения соответствуют наблюдаемые значения посещаемости для врача. Это могут быть следующие характеристики:
4. Степень смещения выборочного среднего, которое определяется величиной коэффициента асимметрии ![]() :
:
![]() (4)
(4)
где ![]() ~ выборочный центральный момент третьего порядка, который определяется по формуле:
~ выборочный центральный момент третьего порядка, который определяется по формуле:
![]() (5)
(5)
Чем ближе значение коэффициента асимметрии ![]() к 0, тем более симметричным является распределение плотности вероятностей и, следовательно, тем ближе закон распределения к нормальному.
к 0, тем более симметричным является распределение плотности вероятностей и, следовательно, тем ближе закон распределения к нормальному.
5. Коэффициент эксцесса, определяющий островершинность распределения среднего, который вычисляется по формуле:
![]() , (6)
, (6)
где ![]() - выборочный центральный момент четвертого порядка.
- выборочный центральный момент четвертого порядка.
6. Медиана (h) - число, которое делит вариационный ряд на две части, содержащие равное кол-во элементов. Если объем выборки n=2k+1 ,то h=xk+1, если n=2k то ![]() .
.
7. Мода d- это элемент, имеющий наибольшую частоту в выборке.
В данной работе проанализированы исходные данные по количеству ежедневных посещений пациентами 8 участковых терапевтов городской поликлиники общего типа и 7 врачей специализированной поликлиники г. Сургута за период 2003-2005 гг. Исходные данные получены при помощи SQL - запросов к базам данных медицинских информационных систем, установленных в лечебно-профилактических учреждениях. Обработка полученных данных проводилась при помощи программ MS Excel и Statistica 6.0. Результаты расчетов для городской поликлиники общего типа представлены в таблице 1.
Таблица 1. Статистические характеристики ежедневной посещаемости участковых терапевтов в городской поликлинике общего типа.
|
Врач |
№1 |
№2 |
№3 |
№4 |
№5 |
№6 |
№7 |
№8 |
Среднее значение по всем врачам |
|
Среднее значение |
24,60 |
20,75 |
23,07 |
25,86 |
29,27 |
20,13 |
23,24 |
21,42 |
23,54 |
|
Стандартное отклонение S |
5,15 |
5,50 |
7,36 |
6,13 |
8,69 |
4,48 |
4,63 |
5,56 |
5,81 |
|
Дисперсия выборки S2 |
26,48 |
30,21 |
54,12 |
37,62 |
44,77 |
29,98 |
21,48 |
30,96 |
34,45 |
|
Мода d |
28 |
20 |
27 |
23 |
26 |
22 |
23 |
23 |
24 |
|
Медиана h |
24,4 |
21,6 |
23,9 |
26,2 |
28 |
22,3 |
22,7 |
23 |
23,9 |
|
Эксцесс К |
0,27 |
-0,05 |
-0,38 |
-0,25 |
-0,44 |
0,10 |
-0,48 |
0,21 |
-0,13 |
|
Асимметричность Sk1 |
0,10 |
0,00 |
-0,33 |
0,11 |
-0,38 |
0,19 |
0,22 |
-0,31 |
0,00 |
|
Интервал
|
19,46 |
15,25 |
15,71 |
19,73 |
23,58 |
13,65 |
18,61 |
15,86 |
17,73 |
|
Интервал
|
29,75 |
26,25 |
30,43 |
31,99 |
34,96 |
26,60 |
27,88 |
26,99 |
29,36 |
Анализ результатов таблицы 1 позволяет сделать вывод о нормальности распределения количества ежедневных посещений врачей ЛПУ общего типа, так как значения коэффициентов асимметрии и эксцесса близки к нулю, а значения среднего, моды и медианы близки. Кроме того, анализируемые данные подчиняются «правилу трех сигм».
Муниципальными органами управления здравоохранением г. Сургута установлено среднее ежедневное количество посещений, приходящееся на одного врача-терапевта - 24 пациента, что соответствует данным, полученным в результате расчета. Расчетные данные показывают, что в среднем количество посещений на одного врача составляет 23,54 при среднеквадратическом отклонение 5,81.
Нормативными документами органов управления установлен средний интервал количества посещений врача на участке, который составляет от 16 до 32 пациентов в день. На основании этих данных рассчитывается функция врачебной должности, то есть количество приемов, которые врач должен оказать за год. Расчеты показывают, что со средней вероятностью 0,68 количество посещений на одном участке в день попадет в интервал 17,73 - 29,36.
Для ЛПУ специализированного типа анализ проводился для 7 врачей, осуществляющих прием пациентов. Результаты первичного статистического анализа представлены в таблице 2.
Таблица 2. Статистические характеристики ежедневной посещаемости врачей в ЛПУ специализированного типа
|
Врач |
№1с |
№2с |
№3с |
Среднее значение по всем врачам |
№4с |
№5с |
№6с |
№7с |
Среднее значение по всем врачам |
|
Среднее значение |
23,33 |
23,46 |
18,70 |
21,83 |
5,09 |
3,56 |
3,58 |
6,30 |
4,64 |
|
Стандартное отклонение S |
9,75 |
7,59 |
9,06 |
8,80 |
3,05 |
1,56 |
1,79 |
4,35 |
2,69 |
|
Дисперсия выборки S2 |
94,99 |
57,61 |
82,14 |
78,24 |
9,29 |
2,44 |
3,20 |
18,89 |
8,45 |
|
Медиана h |
23,4 |
23 |
16 |
24,5 |
3,95 |
3,37 |
3,25 |
5,15 |
3,93 |
|
Мода d |
22 |
21,8 |
18,5 |
20,8 |
3 |
3 |
3 |
5,14 |
3,5 |
|
Эксцесс К |
0,34 |
0,73 |
0,64 |
0,14 |
0,22 |
0,42 |
1,40 |
5,87 |
1,98 |
|
Асимметричность Sk1 |
0,58 |
-0,20 |
0,14 |
0,17 |
0,94 |
0,73 |
1,09 |
2,38 |
1,28 |
|
Интервал
|
13,58 |
15,87 |
9,64 |
13,03 |
2,05 |
2,00 |
1,80 |
1,95 |
1,95 |
|
Интервал
|
33,08 |
31,05 |
27,76 |
30,63 |
8,14 |
5,12 |
5,37 |
10,65 |
7,32 |
В результате расчетов установлено, что все врачи специализированной поликлиники могут быть отнесены к двум разным группам.
Врачи №1с, №2с, №3с относятся к одной группе, так как среднее количество ежедневных посещений у этих врачей достаточно большое, равное 21,83. Данные имеют нормальное распределение с небольшим положительным скосом. Процент попадания в интервал наиболее популярных значений в среднем 64,5%. Во всех трех случаях эксцесс слабо положительный, что показывает более плоское распределение, чем идеальное нормальное.
Врачи №4с, №5с, №6с, №7с были отнесены ко второй группе. Среднее количество ежедневных приемов в этой группе характеризуются малым числом равным 4,64. Коэффициенты асимметрии и эксцесса в сравнении со средними значениями показывают значительное смещение распределения. Врачи, отнесенные нами ко второй группе на основании расчетных данных, как оказалось, являются в специализированном медицинском учреждении врачами-консультантами.
Определение статистической управляемости процесса оказания медицинской помощи
Под задачей статистического управления процессами понимают обеспечение и поддержание процесса на приемлемом и стабильном уровне, гарантируя соответствие продукции или услуг установленным требованиям [5]. Статистически управляемый процесс дает возможность активно вмешиваться в процесс, добиваясь требуемого качества путем целенаправленного изменения исходных параметров.
Из литературы известны различные методы, применяемые для управления качеством, основанные на управленческих инструментами математической статистики: диаграммы Ишикавы, контрольные листки, гистограммы, диаграммы разброса, анализ Парето, стратификация, контрольные карты Шухарта, Хотеллинга и т.п. [6].
Государственным стандартом Российской Федерации определен главный статистический инструмент управления процессами - это контрольная карта Шухарта [5].
Контрольная карта - это графический способ представления информации, основанной на сопоставлении последовательности выборок, отражающих текущее состояние процесса, с границами, установленными на основе внутренне присущей процессу изменчивости.
Назначение системы управления процессом состоит в получении статистического сигнала о наличии особых (неслучайных) причин вариаций. Систематическое устранение особых причин избыточной изменчивости приводит процесс в состояние статистической управляемости. Если процесс находится в статистически управляемом состоянии, качество продукции предсказуемо, и процесс оказания медицинской помощи пригоден для удовлетворения требований, установленных в нормативных документах и медицинских стандартах.
Теория контрольных карт различает два вида изменчивости. Первый вид - это изменчивость из-за «случайных причин», обусловленных бесчисленным набором разнообразных причин, присутствующих постоянно. Сумма всех этих причин измерима и предполагается, что она внутренне присуща процессу. Второй вид - реальные перемены в процессе. Они могут быть следствием некоторых определяемых причин, не присущих процессу внутренне и могут быть устранены. Эти выявляемые причины рассматриваются как «неслучайные» или «особые» причины изменения. В процессе оказания медицинской помощи к ним могут быть отнесены недостаточная квалификация персонала, поломка инструментов, нарушение регламента, невыполнение необходимых медицинских процедур, недостатки в организации процесса.
Цель контрольных карт - обнаружить неестественные изменения в данных из повторяющихся процессов и дать критерии для обнаружения отсутствия статистической управляемости. Процесс находится в статистически управляемом состоянии, если изменчивость вызвана только случайными причинами.
Карта Шухарта требует данных, получаемых выборочно из процесса через примерно равные промежутки времени.
Для каждой подгруппы определяют статистические характеристики:
- среднее арифметическое в подгруппе ( ![]() );
);
- размах подгруппы R= Хmax-Xmin.
Карта Шухарта - это график значений определенных характеристик подгрупп в зависимости от их номера. Она имеет центральную линию (CL), соответствующую эталонному значению характеристики. При оценке того, находится ли процесс в статистически управляемом состоянии, эталоном обычно служит среднее арифметическое рассматриваемых данных или заранее установленное нормативное значение.
Карта Шухарта имеет две статистические определяемые контрольные границы относительно центральной линии, которые называются верхней контрольной границей (UCL) и нижней контрольной границей (LCL) (рис. 1).
Контрольные границы находятся на расстоянии ±3σ от центральной линии, где σ - генеральное стандартное отклонение используемой статистики. Граница ±3σ указывает, что около 99,7% значений характеристики подгрупп попадут в эти пределы при условии, что процесс находится в статистически управляемом состоянии. [5].
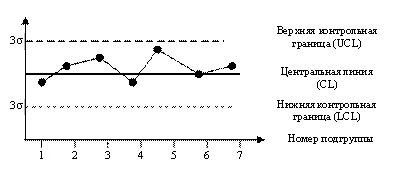
Рис. 1. Вид контрольной карты
Считается, что процесс находится в статистически управляемом состоянии, если точки разбросаны вокруг центральной линии, находятся в контрольных пределах, нет серий и трендов.
Построение контрольных карт и необходимые расчеты производились при помощи ППП Microsoft Excel, стандартных функций программы и специально разработанного программного модуля (макроса) по следующему алгоритму:
- При помощи SQL запроса получить исходные данные за рассматриваемый период из базы данных информационной системы ЛПУ и поместить данные в группы по четыре элемента в таблице Excel.
- Для каждой подгруппы определить среднее арифметическое в подгруппе (
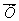 ).
). - Определить среднее арифметическое и стандартное отклонение для
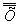 .
. - Определить контрольные границы для карты средних: центральную линию (CL), которая равна , верхнюю контрольную границу (UCL), нижнюю контрольную границу (LCL) (табл.3).
- Определить размах подгруппы R.
- Определить среднее арифметическое и стандартное отклонение для R.
- Определить контрольные границы для карты размахов: центральную линию (CL), которая равна
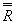 , верхнюю контрольную границу (UCL), нижнюю контрольную границу (LCL) (табл. 3).
, верхнюю контрольную границу (UCL), нижнюю контрольную границу (LCL) (табл. 3). - Построить карту средних и карту размахов.
- Сопоставить нанесенные точки средних и размахов с контрольными границами, выделить точки вне контрольных границ, необычные структуры и тренды, которые свидетельствуют о выходе процесса из статистически устойчивого состояния.
- Для каждого сигнала о выходе процесса из статистически устойчивого состояния провести анализ и определить причину выхода процесса из статистически управляемого состояния.
Таблица 3. Формулы для расчета контрольных границ карт Шухарта
|
Статистика |
Центральная линия (CL) |
Верхняя контрольная граница (UCL) |
Нижняя контрольная граница (LCL) |
|
|
|
|
|
|
|
|
|
|
Коэффициенты A, D1, D2 в таблице 3 для вычисления линий контрольных карт приведены в ГОСТ Р 50779.42-99 [5] и зависят от числа наблюдений в подгруппе.![]() и
и ![]() - средние значения для наблюдаемого параметра и размаха значений параметра в подгруппе,
- средние значения для наблюдаемого параметра и размаха значений параметра в подгруппе, ![]() и
и ![]() - средние арифметические средних значений в подгруппах, S - стандартное отклонение среди средних процесса.
- средние арифметические средних значений в подгруппах, S - стандартное отклонение среди средних процесса.
По имеющимся экспериментальным данным за 2003-2005 гг. специализированной поликлиники и для поликлиники общего типа г. Сургута построены контрольные карты Шухарта для коэффициента интенсивности работы врача (участкового терапевта ЛПУ общего типа и врача узкой специализации), который был рассчитан по формуле
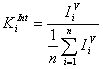 (7)
(7)
где ![]() - интенсивность нагрузки i - того врача, которая определяется, как:
- интенсивность нагрузки i - того врача, которая определяется, как:
![]() ,
,
где B - число пролеченных больных за анализируемый период времени; T- фактически отработанное время
По введенным в электронную таблицу исходным данным рассчитывались значения контролируемых статистик: средние ![]() и размах
и размах ![]() .
.
На рис. 2 - 3 приведены результаты расчетов. Рисунок 2 демонстрирует контрольные карты интенсивности работы Врача №1с специализированной поликлиники. Кривые коэффициента интенсивности не выходят за контрольные границы, трендов не наблюдается и, следовательно, процесс оказания медицинской помощи для данного специалиста находится в статистически устойчивом состоянии.
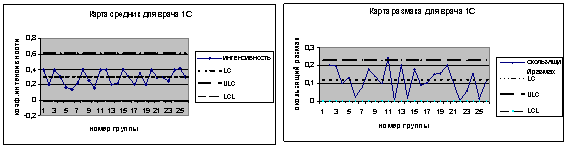
Рис. 2. Карта Шухарта для коэффициента интенсивности Врача №1с специализированного ЛПУ
Следует отметить, что статистически управляемое состояние процесса свидетельствует не только об отличной работе исполнителей процесса, но и хорошей организации процесса, наличии необходимого оборудования и условий работы.
На рис. 3 представлены контрольные карты, рассчитанные для Врача №5 ЛПУ общего типа. Кривая размаха ![]() выходит за контрольные границы, что свидетельствует о статистической неустойчивости процесса оказания медицинской помощи в определенный период времени для данного врача.
выходит за контрольные границы, что свидетельствует о статистической неустойчивости процесса оказания медицинской помощи в определенный период времени для данного врача.
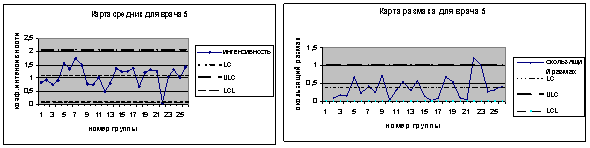
Рис. 3. Карта Шухарта для коэффициента интенсивности Врача №5 ЛПУ общего типа
Статистически неустойчивое состояние процесса может быть связано с наличием высокой интенсивности нагрузки у Врача №5. Об этом свидетельствуют расчетные данные таблицы 1. Возможно, что причина кроется в чем-то другом. Изучение и анализ статистически неуправляемого процесса - это миссия специалистов, занимающихся управлением лечебно-профилактическим учреждением.
СПИСОК ЛИТЕРАТУРЫ:
- Васильев В.Н. Модели управления вузом на основе информационных технологий / В.Н. Васильев - Петрозаводск: Изд-во ПетрГУ, 2000.-164с.:ил.
- ГОСТах 40.9001-03-87.88
- ИСО 9001-9003-87
- Вентцель Е.С., Теория случайных процессов и ее инженерные приложения: Учеб. пособие для студ. втузов /Е.С. Вентцель, Л.А. Овчаров. - 3-е изд., перераб. и доп. - М.: Издательский центр «Академия», 2003. - 432 с.
- ГОСТ Р 50779.42-99 Статистические методы. Контрольные карты Шухарта.
- Клячкин В.Н. Технология многомерного статистического контроля процесса //Информационные технологии в проектировании и производстве, 2002, №1, с.49-53.
Библиографическая ссылка
Алмазова Е.Г., Иванникова Е.Н., Микшина В.С., Улитина И.В. ОПТИМИЗАЦИЯ УПРАВЛЕНИЯ В ЗДРАВООХРАНЕНИИ НА ОСНОВЕ СТАТИСТИЧЕСКИХ МОДЕЛЕЙ // Современные проблемы науки и образования. 2007. № 6-1. ;URL: https://science-education.ru/ru/article/view?id=711 (дата обращения: 20.12.2025).



