В операциях цифровой обработки сигналов особое внимание уделяется цифровой фильтрации, которая может занимать более половины всего объёма вычислений. В узком смысле цифровой фильтр - это частотно-избирательная цепь, обеспечивающая селекцию цифровых сигналов по частоте [1]. После выполнения цифровой фильтрации мы, как правило, получаем интересующий нас сигнал, т.е. сигнал, несущий нужную нам информацию, в виде, удобном для последующей обработки. Соответственно, к параметрам цифровых фильтров в современных системах цифровой обработки сигналов начинают предъявляться повышенные требования. Порядки фильтров нередко достигают тысячи и более. Это ведёт к увеличению объёма вычислений, а значит, и к резкому росту аппаратных затрат. При синтезе цифровых фильтров наибольшие затраты времени и оборудования приходятся на операции умножения. Таким образом, задача минимизации времени вычислений и уменьшения аппаратных затрат сводится к минимизации количества умножений, требуемых для вычисления очередного отфильтрованного отсчёта.
Структура фильтра
Все цифровые фильтры делятся на два обширных класса: нерекурсивные - фильтры с конечной импульсной характеристикой (КИХ), и рекурсивные - фильтры с бесконечной импульсной характеристикой (БИХ). Мы будем рассматривать только КИХ-фильтры, фазовая характеристика которых, в отличие от БИХ-фильтров, линейна. КИХ-фильтры описываются следующим выражением [5]:
 (1)
(1)
где y(n) - сигнал на выходе фильтра; x(n) - сигнал на входе фильтра; bi - коэффициенты фильтра.
Таким образом, задача синтеза КИХ-фильтра сводится к вычислению коэффициентов bi такого фильтра.
Проблема минимизации количества операций умножения может быть решена различными путями. Одним из путей является использование неклассических структур цифровых фильтров, которые бы описывались выражениями, отличными от (1), и в которых операция умножения исключена вообще. Такие структуры позволяют для некоторых классов цифровых фильтров обеспечить улучшенные характеристики при их реализации [2, 3, 4]. Рассмотрим одну из упомянутых структур. В её основе - субструктура, изображённая на рис.1 [1].

Рис. 1 - Структурная схема элементарного звена
Где K - количество задержек; W - весовой коэффициент (количество сумматоров). Каскадным соединением таких субструктур можно синтезировать фильтры, обладающие различными амплитудно-частотными характеристиками, которые бы удовлетворяли заданным требованиям по таким критериям, как ширина полосы пропускания фильтра, подавление боковых лепестков, прямоугольность и т.д. [2, 3, 4].
Расширим класс элементарных структур, введя структуру второго порядка (рис.2):

Рис.2 - Элементарное звено с коэффициентом
АЧХ структуры будет иметь одну "точку подавления", которая перемещается по частотному диапазону в зависимости от значения коэффициента k.
Очевидно, что в случае уменьшения коэффициента k точка подавления сдвигается влево по оси частот, а при увеличении - вправо. Таким образом, введением звена с коэффициентом можно влиять на положение точки подавления, регулируя тем самым равномерность частотной характеристики в полосе подавления.
Отметим, что, введя звено второго порядка, мы тем самым «перекинули мостик» между жёсткой структурой фильтров без умножителей и гибкой, но медленной структурой классических ЦФ. Два-три таких звена легко устраняют недостатки новой структуры и очень незначительно сказываются на быстродействии.
Синтез фильтров с оптимальными параметрами
Для получения фильтра, эффективного для определённого рода задач, необходимо знать параметры элементарных звеньев, составляющих фильтр, а также количество этих звеньев. Эту задачу можно решать двумя путями.
Один из путей - это перебор возможных комбинаций каскадного соединения элементарных звеньев для получения фильтра с требуемыми параметрами. В этом случае задаются наиболее приоритетные параметры фильтра - один или несколько, значения которых и будут являться критериями для перебора. Такой перебор можно сократить введением ограничения на максимальное число элементарных звеньев или задержек.
Другой путь, который представляется наиболее перспективным, - это изначальное задание требований к АЧХ фильтра и получение по заданным требованиям к АЧХ фильтра его структуры, то есть комбинации элементарных звеньев с известными АЧХ. В этом случае мы сначала синтезируем фильтр с заданной АЧХ (например, с помощью утилиты fdatool среды Matlab), получаем коэффициенты его импульсной характеристики, округляем их, где это необходимо, записываем уравнение передаточной функции фильтра в виде полинома степени n, а затем по имеющемуся полиному, пользуясь закономерностями, рассмотренными выше, строим структуру фильтра без умножителей. Естественно, что это не всегда возможно сделать точно, и структура фильтра может быть получена с некоторыми допущениями и приближениями.
Рассмотрим фильтр, полученный каскадным соединением элементарных звеньев, подобранных из соображений получения максимального подавления его боковых лепестков (первый путь). АЧХ этого фильтра представлена на Рис. 3.
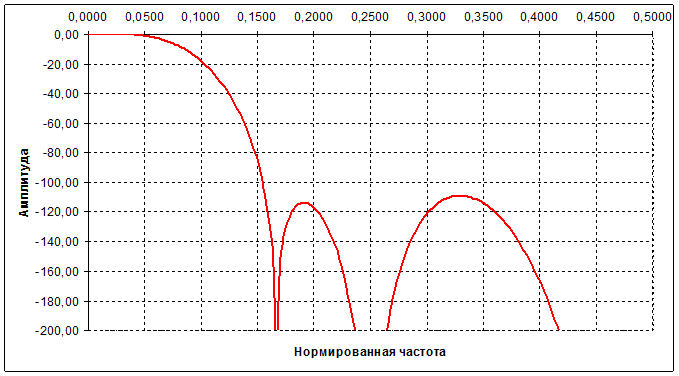
Рис. 3 - АЧХ синтезированного фильтра
Как видно, мы получили фильтр нижних частот (ФНЧ) с конечной импульсной характеристикой (КИХ). У этого фильтра количество элементарных звеньев равно 44. Ширина полосы пропускания по критерию 3дБ равна 0,062ω. Подавление боковых лепестков 109 дБ.
Синтезируем фильтр с вышеперечисленными параметрами с помощью утилиты fdatool среды Matlab. Получился фильтр нижних частот (ФНЧ) с конечной импульсной характеристикой (КИХ), порядок которого равен 74.
Рассмотрим теперь пример синтеза фильтра без умножителей по сгенерированной характеристике (второй путь). Синтезируем фильтр нижних частот с заданными параметрами: неравномерность в полосе пропускания 1дБ, максимальный уровень боковых лепестков -25 дБ, относительная ширина полосы пропускания 0.4, относительная ширина полосы задерживания 0.5, с помощью утилиты fdatool. Получим фильтр двадцатого порядка.
На рис. 4 представлена нормированная импульсная характеристика синтезированного фильтра, и она же, но округленная до целого числа. Собственно, наш «фильтр без умножителей» без умножителей будет реализовывать эту округленную характеристику. Очевидно, что при этом точность аппроксимации и трудоемкость процесса синтеза фильтра (а в нем все еще сильна доля эвристики) напрямую зависят от нормировочного коэффициента (в нашем примере он равен 20). На рис. 5 показаны АЧХ исходная и приближенная.

Рис. 4 - Импульсные характеристики: исходная и приближенная

Рис. 5 - Частотные характеристики исходного фильтра и приближенного
Составим таблицу (табл. 1), в которую запишем коэффициенты будущего фильтра. Далее, разложим импульсную характеристику на сумму полиномов так, чтобы каждый полином можно было легко реализовать каскадным соединением элементарных звеньев. Естественно, такое разложение не является единственным. Каждый полином будет реализован в отдельной ветви фильтра, а сложение ПФ ветвей даст импульсную характеристику синтезируемого фильтра.
Табл. 1 - Коэффициенты синтезируемого фильтра
|
Номер коэф-та |
20 |
19 |
18 |
17 |
16 |
15 |
14 |
13 |
12 |
11 |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
|
Коэф. |
1 |
0 |
-1 |
0 |
1 |
1 |
-1 |
-2 |
1 |
6 |
9 |
6 |
1 |
-2 |
-1 |
1 |
1 |
0 |
-1 |
0 |
1 |
|
Ветвь 1 |
1 |
0 |
-1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
-1 |
0 |
1 |
|
Ветвь 2 |
|
|
|
|
|
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
Ветвь 3 |
|
|
|
|
|
|
-1 |
-2 |
-1 |
0 |
0 |
0 |
-1 |
-2 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
Ветвь 4 |
|
|
|
|
|
|
|
|
2 |
6 |
8 |
6 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Запишем передаточные функции для каждой ветви:
 (2)
(2)
Структура фильтра, реализованного в MATLAB Simulink, представлена на рис. 6. Некоторые звенья в разных ветвях повторяются, и приведенная структура может быть упрощена, однако для простоты и экономии места оставлена в виде, соответствующем передаточным функциям (2).

Рис.6 - Структура фильтра в MATLAB Simulink
При составлении ПФ мы пользовались несколькими простыми, но эффективными приемами.
Во-первых, т.к. импульсная характеристика КИХ фильтра с линейной фазой симметрична, то часто ПФ ветви тоже оказывается симметричной (в данном случае, это верно для всех ветвей, но это, конечно, не правило). Поэтому удобным бывает «копирование» полинома низкого порядка с помощью звена с ![]() , как это сделано, например, в первой и третьей ветви.
, как это сделано, например, в первой и третьей ветви.
Во-вторых, сгенерированная ПФ ветви может быть легко «сдвинута» по импульсной характеристике простым добавлением множителя (звена) ![]() .
.
В-третьих, несмотря на то, что рассматривается класс фильтров без умножителей, можно смело использовать коэффициенты, если они равны 2i, т.к. формально умножение на 2 эквивалентно сдвигу двоичного числа на 1 бит влево.
И, наконец, в-четвертых, полезно использовать древовидные структуры, наподобие «треугольника Паскаля». Однако удобным оказывается использование «деревьев», в основе которых лежит больше одного коэффициента. Например, рассмотрим «дерево», в основании которого три коэффициента - a,b,c:

Такое «дерево» использовалось, например, при выборе ПФ ветви 4. Рассмотрим случаи, когда (a,b,c)= (1;0;0) ,(0;1;0) , (0;0;1). Как видно, в представленном «abc-дереве» остаются только соответствующие единицам коэффициенты. Если сравнить их с «треугольником Паскаля», то мы увидим, что они абсолютно совпадают.
Таким образом, вне зависимости от выбора основы (значения, количества и взаимного распределения коэффициентов {a,b,c,...}) в результате получим сумму коэффициентов пересекающихся деревьев.
Для упрощения задачи разложения можно поступить следующим образом: импульсная характеристика округляется до ближайшего числа, равного 2n, и синтезируется структура, реализующая такую аппроксимацию. Можно повторить эту процедуру несколько раз, используя на каждом следующем шаге разность между целевой и приближенной характеристикой, а оставшуюся в конце разность разложив так, как это показано в примере. Такой подход кажется целесообразным при синтезе фильтров большого порядка.
Заключение
Мы рассмотрели два способа синтеза фильтров без умножителей.
Первый подразумевает получение желаемой частотной характеристики путем последовательного соединения типовых звеньев aZ-K±a, задав первый ноль ЛАЧХ и подавив все в полосе задерживания. При этом, повторение двух одинаковых звеньев приводит к усилению подавления.
Второй способ нацелен на аппроксимацию импульсной характеристики сгенерированного с помощью специальных программных средств фильтра (например, FDAtool из MATLAB). Импульсная характеристика раскладывается на сумму полиномов, каждый из которых реализуется последовательным соединением звеньев («ветвь» фильтра), а параллельное соединение ветвей даст желаемую импульсную характеристику. Для упрощения задачи синтеза структуры фильтра предлагается использовать «деревья» (треугольник Паскаля), получаемые с помощью последовательного соединения звеньев Z-1+1, и их комбинации (abc-деревья). Также для упрощения предложено использовать аппроксимацию импульсной характеристики с помощью «округления» до 2n.
Рецензенты:
- Куприянов М.С., доктор технических наук, профессор, профессор кафедры ВТ ФГБОУ ВПО «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина)», г. Санкт-Петербург.
- Дмитревич Г.Д., доктор технических наук, профессор, профессор кафедры САПР ФГБОУ ВПО «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина)», г. Санкт-Петербург.
Библиографическая ссылка
Каплун Д.И. РАЗРАБОТКА И ИССЛЕДОВАНИЕ НЕРЕКУРСИВНЫХ ЦИФРОВЫХ ФИЛЬТРОВ БЕЗ УМНОЖЕНИЙ // Современные проблемы науки и образования. 2012. № 4. ;URL: https://science-education.ru/ru/article/view?id=6691 (дата обращения: 24.02.2026).



