По результатам статистических исследований аномалий геофизических полей магнитной и гравитационной природы в пределах изучаемой территории установлена блоковая структура земной коры [4] в виде ромбических структур, что отражает общие закономерности строения литосферы [3].
При изучении закономерностей сейсмического процесса Олекмо - Становой зоны было установлено, что в динамике сейсмичности содержатся периодические компоненты. Этот результат свидетельствует о том, что динамическая функция состояния массива горных пород (энергонасыщенность) должна содержать периодические компоненты вида
|
|
(1) |
где ![]() ,
, ![]() - энергетический и периодический параметры сейсмической активности, формирующиеся под действием внешней силовой нагрузки
- энергетический и периодический параметры сейсмической активности, формирующиеся под действием внешней силовой нагрузки ![]() ;
; ![]() - количество разнородных силовых нагрузок.
- количество разнородных силовых нагрузок.
Статистический анализ распределений количества сейсмических событий на различных периодах реализаций показал, что неоднородность сейсмической активности наиболее контрастно проявляется на суточных и недельных периодах. Фактически это означает, энергонасыщенность массива горных пород (1) можно аппроксимировать функциями вида
|
|
(2) |
где k1 = 1,2,..., 24 - дискретное время (часы суток) и аналогично для недельной статистики
|
|
(3) |
где k2 = 1,2,..., 7 - дискретное время (дни недели).
Изменение энергонасыщенности массива горных пород в виде функций распределения (2) - (3) связано с действием внешней силовой нагрузки и, как следствие, с деформацией геофизической среды [3].
Источником суточных аномалий (2) могут быть силы инерции, связанные с неравномерностью суточного вращения Земли, и как следствие, с изменением кинематики взаимодействия блоков земной коры. Для недельных аномалий (3) - причиной может быть семидневная цикличность техногенной нагрузки на геологическую среду посредством массовых взрывов.
Фактически это означает, что необходимо рассмотреть задачи о движении блоков под действием внешней периодической силовой нагрузки в потенциальном поле силы трения. Данные задачи определили цель настоящего исследования, направленную на построение моделей движения блоков земной коры под действием слабых возмущений.
Результаты моделирования
Поставленная задача о движении (относительном) блоков может быть рассмотрена в одномерном случае, если из всего набора шовных межблоковых зон одна отличается по своим физическим свойствам (верхний фрагмент, рис.1). В этом случае, выбирая направление оси x вдоль данного контакта и проецируя все векторные величины на данное направление, получим одномерную модель.
Если рассматривать границу раздела блоков как тривиальный трибологический контакт, то для анализа движения блока в режиме «stick-slip» по контакту можно использовать формализм обобщенной одномерной модели Томлинсона [5], разработанной для изучения процессов трения. В рамках этой модели рассматривается одномерное движение тела с массой m под действием силы F в поле периодической потенциальной силы сопротивления c амплитудой N и периодом a. Уравнение движения тела имеет вид:
|
|
(4) |
где ![]() - вязкость среды, x - координата тела. Если ввести новые безразмерные переменные
- вязкость среды, x - координата тела. Если ввести новые безразмерные переменные ![]() и
и ![]() , то
, то ![]() ,
, ![]() , и уравнение (4) может быть переписано как
, и уравнение (4) может быть переписано как
|
|
(5) |
где ![]() - безразмерная сила,
- безразмерная сила, ![]() - безразмерный коэффициент затухания.
- безразмерный коэффициент затухания.
Теперь рассмотрим трибологическую систему (рис.1, нижний фрагмент), состоящую из двух блоков массой m и M, разделенных межблоковой шовной зоной, тонкой пленкой между блоками (трибологический контакт). Блок m имеет возможность двигаться относительно блока M за счет внешней силы F1 в поле силы F2. Блок M соединен с основанием двумя пружинами с коэффициентом жесткости k. Пусть сила F1, вызывающая смещение блока m, изменяется по периодическому закону ![]() . Проекции этой силы равны
. Проекции этой силы равны ![]() на ось x и
на ось x и ![]() на направление силы F2, где γ - угол между направлением действия силы F1 и осью x. Координату его центра тяжести
на направление силы F2, где γ - угол между направлением действия силы F1 и осью x. Координату его центра тяжести ![]() относительно неподвижной системы координат и скорость движения блока
относительно неподвижной системы координат и скорость движения блока ![]() можно записать в виде
можно записать в виде ![]() ,
, ![]() . В этом случае сила трения Fтр будет зависеть от нагрузки N( F2, F1) нелинейным образом (периодический потенциал).
. В этом случае сила трения Fтр будет зависеть от нагрузки N( F2, F1) нелинейным образом (периодический потенциал).
Действительно, если упруго-вязкие свойства контакта не меняются за период действия силы F1, то силу трения можно представить в виде суммы 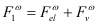 , где
, где ![]() - упругая и
- упругая и ![]() - пластическая составляющие силы трения. Пусть
- пластическая составляющие силы трения. Пусть ![]() - коэффициент трения в отсутствие периодической силы, тогда силу
- коэффициент трения в отсутствие периодической силы, тогда силу ![]() можно представить в виде
можно представить в виде
![]()
где ![]() периодическая компонента коэффициента трения. Сила
периодическая компонента коэффициента трения. Сила ![]() пропорциональна скорости движения блока в первой степени
пропорциональна скорости движения блока в первой степени ![]() , где η - вязкость среды контакта.
, где η - вязкость среды контакта.
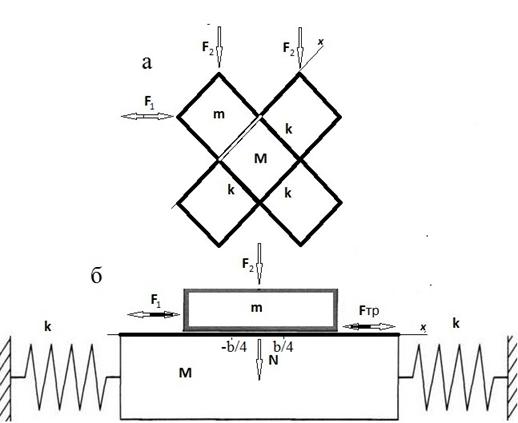
Рис. 1. Блоковая (а) и трибологическая (б) модели движения блока. Обозначения в тексте
Если контакт не однороден, то дополнительно к силе ![]() появится сила трения
появится сила трения ![]() , пропорциональная линейному размеру неоднородности b=L/2n, где L - линейный размер блока, n=1, 2, 3,... .
, пропорциональная линейному размеру неоднородности b=L/2n, где L - линейный размер блока, n=1, 2, 3,... .
|
|
(6) |
Под действием силы ![]() блок М начнет движение. Уравнение движения блока будет зависеть от силы горизонтального сжатия F2 (направление силы выбрано условно), которую за период действия силы F1 можно принять постоянной и сил упругости
блок М начнет движение. Уравнение движения блока будет зависеть от силы горизонтального сжатия F2 (направление силы выбрано условно), которую за период действия силы F1 можно принять постоянной и сил упругости ![]() при взаимодействии с соседними блоками.
при взаимодействии с соседними блоками.
Таким образом, уравнение движения (4) с учетом (6) можно записать в виде
|
|
(7) |
Если блоки расположены горизонтально, то роль нагрузки играет нормальная проекция силы горизонтального сжатия . Отличие двух положений блоков заключается в том, что при вертикальном расположении Fтр ≤ N(m). В горизонтальном положении сила трения не зависит от массы подвижного блока, и сила трения может принимать любое значение (в зависимости от величины ).
Ограничением горизонтального смещения без проскальзывания служат максимумы ![]() в точках ±
в точках ±![]() (см. рис.1). При дальнейшем увеличении x движение переходит в режим «stick-slip», то есть блок из одной потенциальной ямы переходит в другую. При этом величина смещения
(см. рис.1). При дальнейшем увеличении x движение переходит в режим «stick-slip», то есть блок из одной потенциальной ямы переходит в другую. При этом величина смещения ![]() будет пропорциональна (± b/4), т.е.
будет пропорциональна (± b/4), т.е. ![]() , где k = 0,1,2,... Этот режим может наблюдаться и при изменении физических параметров контакта, как это показано в работе [1] при изучении движения блоков в режиме «stick-slip», в пределах
, где k = 0,1,2,... Этот режим может наблюдаться и при изменении физических параметров контакта, как это показано в работе [1] при изучении движения блоков в режиме «stick-slip», в пределах ![]() изменения силы трения.
изменения силы трения.
Уравнение (7) обобщает уравнение (4) и эквивалентно ему при отсутствии сил дальнодействия ![]() и периодической нагрузки
и периодической нагрузки ![]() . Сравнивая уравнение математического маятника [2, стр. 487] и уравнение (5), можно заключить, что уравнение (5) описывает затухающие колебания, когда затухание пропорционально первой степени скорости. Переход колебательного движения блоков в поступательное (в режим «stick-slip») возможен при уменьшении сил трения (6) вследствие изменения физических свойств контакта.
. Сравнивая уравнение математического маятника [2, стр. 487] и уравнение (5), можно заключить, что уравнение (5) описывает затухающие колебания, когда затухание пропорционально первой степени скорости. Переход колебательного движения блоков в поступательное (в режим «stick-slip») возможен при уменьшении сил трения (6) вследствие изменения физических свойств контакта.
Рецензенты:
Максимов Евгений Петрович, доктор геолого-минералогических наук, профессор по кафедре ТИТР, Технический институт (филиал) ФГАОУ ВПО "Северо-Восточный федеральный университет имени М.К. Аммосова", г. Нерюнгри.
Заровняев Борис Николаевич, доктор технических наук, профессор, декан Горного факультета Северо-Восточного федерального университета, г. Якутск.
Библиографическая ссылка
Трофименко С.В., Гриб Н.Н. ГЕОМЕХАНИЧЕСКАЯ МОДЕЛЬ БЛОКОВОГО ДВИЖЕНИЯ ЗЕМНОЙ КОРЫ // Современные проблемы науки и образования. 2012. № 3. ;URL: https://science-education.ru/ru/article/view?id=6462 (дата обращения: 18.02.2026).




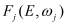 ≈
≈