При создании композиционных материалов (КМ), как правило, требуется обеспечить соответствие целого ряда свойств заданным значениям [1]. При этом показатель каждого из свойств должен попадать в ограниченный коридор допустимых значений, максимально приближаясь к оптимальной величине. При такой постановке задачи выбор условий получения КМ, оптимально соответствующего требованиям становится достаточно сложным, даже если известна зависимость, определяющая значение каждого свойства как функцию от условий получения.
Экспериментальное решение задачи путем подбора необходимой рецептуры и технологии получения процесс длительный и дорогой. Возможной альтернативой может быть создание вычислительной методики, основанной на построении модели, отражающей зависимость комплекса свойств КМ от условий его получения.
Ставится задача разработать технологию получения на основе заданного набора компонентов и фиксированного списка модифицирующих воздействий композитного материала (КМ), обладающего комплексом регламентируемых свойств, максимально близким к заданному.
Нами была предложена следующая постановка указанной задачи [2]: комплекс условий c={c1,…,cm} (cÎC) обеспечивает получение материала, обладающего комплексом характеристик p={p1,…,pn} (pÎP). Задано p*-оптимальное значение вектора p. Полагая известным оператор отображения C на P {F(c)=p}, найти c*, для которого:
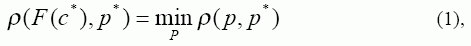
где ρ – расстояние между векторами в некоторой мере.
Для решения этой оптимизационной задачи предложена информационная технология[2], включающая:
- построение по результатам эксперимента оператора отображения C на P {F(c)=p};
- выбор критерия качества ρ, определяющего близость комплекса свойств КМ, рассчитанного для выбранных условий получения, к заданному комплексу свойств;
- определение P - области допустимых значений в пространстве свойств КМ;
- выбор возможной стратегии поиска оптимума c* в зависимости от используемого плана эксперимента.
Для получения оператора F необходимо провести эксперимент по плану D, в результате которого будет получен набор образцов КМ, каждый из которых обладает комплексом свойств pi (i=1,…,k). Объединим результаты измерения свойств в матрицу Р -матрица, строки которой суть соответствующие векторы рi. Тогда, полагая линейной зависимость Р от D, будем искать F на классе матриц вида:

где D+ - матрица, псевдообратная к D. Адекватность F оценивается по выполнению неравенства:

где e - выбранный порог, |.| - М-норма матрицы.
Если неравенство (3) не выполняется, то матрица D модифицируется путем добавления к ней столбцов, полученных по соотношению:
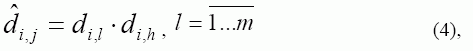
где di,l, di,h- элементы исходной матрицы плана, а ![]() - элемент расширенной матрицы плана.
- элемент расширенной матрицы плана.
В качестве меры выбран обобщенный критерий качества, получаемый следующим образом [4]. Для каждого свойства композита задаются три значения: максимальное ymax, минимальное ymin и наилучшее yopt, при условии ymin < yopt < ymax. Значение частного критерия качества для этих значений принимается равным соответственно 0, 0 и 1. Для отрезков ymin - yopt и yopt - ymax определяются интерполирующие полиномы Ньютона третьего порядка [5], вычисленные при условии, что первые производные на концах отрезков равны нулю. Частный критерий качества строится склеиванием полученных полиномов Ньютона, причем условие равенства нулю производных в точке yopt обеспечивает их гладкую склейку.
Обобщенный критерий качества строится в виде взвешенного произведения частных критериев качества
p=
где ri–значения частных критериев качества, а ai- их веса. Построенный таким образом обобщенный критерий качества обращается в нуль за пределами P -области допустимых значений свойств КМ.
Разработана программная оболочка [3], обеспечивающая управление процессом, которая предусматривает следующие стратегии оптимизации. В пространстве вещественных признаков (регрессионный план) используется симплексный поиск или метод сопряженных градиентов. При оптимизации в булевом пространстве (дисперсионный план) реализуется обход вершин единичного куба и выбор вершины, соответствующей экстремальному значению функции качества. В случае ковариационной матрицы плана, используется комбинация этих стратегий, т. е. обход вершин гиперкуба, соответствующих строкам дисперсионной части ковариационного плана, и поиск экстремума в вещественном пространстве, соответствующем регрессионной части плана для соответствующей вершины.
Применение описанной процедуры для поиска оптимальных условий получения композитного резистивного материала [4] подтвердило высокую эффективность описанной технологии.
СПИСОК ЛИТЕРАТУРЫ
1. Калинина Э.В., Лапига А.Г., Поляков В.В. и др. Оптимизация качества. Сложные процессы. – М.: Химия, 1989.-256с.
2. О.Н. Вылегжанин, В. П.Григорьев, П.С. Чубик, О.В. Доценко Информационная технология создания композитных материалов, обладающих свойствами, максимально близкими к заданным //Материалы IIIвсероссийской научной конференции «Химия и химическая технология на рубеже тысячелетий», Томск, 2-4 сентября 2004г, с 265.
3. О.В. Доценко, О.Н. Вылегжанин Разработка программной оболочки для реализации информационной технологии создания композитных материалов. //Сборник трудов III всероссийской научно - практической конференции студентов «Молодежь т современные информационные технологии», Томск, 15-17 февраля 2005г, с 55-56.
4. Minakova N.n., Ushakov V.Ja., Vylegzhanin O.N. «Choice Method of Resistive Composite Materials with the Specified Complex of Properties” 5-th Korea-Russia International Symposium on Science and Technology, Tomsk, 2000, pp.215-217
5. Де Бор К. Практическое руководство по сплайнам. – М.: Радио и связь. – 1985. – 304с.
Библиографическая ссылка
Вылегжанин О.Н. ИНФОРМАЦИОННАЯ ТЕХНОЛОГИЯ ПОЛУЧЕНИЯ НА ОСНОВЕ ЗАДАННОГО НАБОРА КОМПОНЕНТОВ КОМПОЗИТНОГО МАТЕРИАЛА, ОБЛАДАЮЩЕГО КОМПЛЕКСОМ СВОЙСТВ, МАКСИМАЛЬНО БЛИЗКИМ К ЗАДАННОМУ // Современные проблемы науки и образования. 2006. № 6. ;URL: https://science-education.ru/ru/article/view?id=610 (дата обращения: 06.03.2026).



