В язык размётки гипертекста [ 1, 2 ], используемый для построения электронного курса “ Нечёткая логика и её применение “ встраивается классический язык LJ (логика интуиционистская Генцена) с целью формализации доказательств и автоматического построения различных интерпретаций в соответствии с теорией моделей. Основная секвенция берётся в виде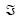 
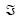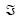→, где - произвольная формула, интерпретируемая в модели M (различные алгебры, изучаемые в работе) как (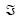) M = F – формула алгебры, (→) M = ⊃ - импликация алгебры. Таким образом, основная секвенция в модели M имеет вид: F ⊃ F, являясь тождественно – истинной формулой.
Рассмотрим фигуру заключения, называемую утончением в антецеденте:
где G - список формул 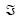1,......, 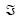n, Δ - список с не более, чем одной формулой. Для модели M (1) принимает вид:
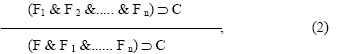
где C – интерпретация формулы списка Δ, (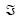 i) M = F i.
Покажем, что если в числителе (2) формула тождественно – истинная, то и в знаменателе она тождественно – истинная. Доказательство проводим методом от противного : предположим, что существует такой набор переменных из области интерпретации M, что формула в знаменателе (2) обращается в ложь:
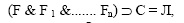
поскольку импликация обращается в ложь тогда и только тогда, когда посылка истинна : F & F 1 &...... F n = И, а заключение ложно : С = Л, то F = И, F 1 = И,...., F n = И, но при этих значениях формул числитель в (1) обратится в ложь, что противоречит предположению. Аналогичным образом можно дать обоснование остальным правилам вывода (фигурам заключения в LJ), так как они имеют вид
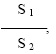
где S 1, S 2 - секвенции. (Методом от противного доказывается : если интерпретация S 1 – тождественно истинная формула, то и интерпретация S 2 тоже тождественно – истинная формула). Рассматривается постановка и реализация этих доказательств на ЭВМ.
СПИСОК ЛИТЕРАТУРЫ
1. Тарушкин В.Т., Тарушкин П.В., Тарушкина Л.Т. Информационная технология построения электронного курса “ Нечёткая логика и её применение “. Электронная конференция РАЕН 5 – марта 2006 г.
2. Графика в информационной технологии электронного курса “Нечёткая логика и её применение “. IV Общероссийская конференция с международным участием “Новейшие технологические решения и оборудование” 11 – 13 мая 2006 г. Моква (в печати).
Библиографическая ссылка
Тарушкин В.Т., Тарушкин П.В., Тарушкина Л.Т. МЕТОДЫ ТЕОРИИ ДОКАЗАТЕЛЬСТВ И ТЕОРИИ МОДЕЙ В ТЕХНОЛОГИИ ЭЛЕКТРОННОГО КУРСА “ НЕЧЁТКАЯ ЛОГИКА И ЕЁ ПРИМЕНЕНИЕ” // Современные проблемы науки и образования. 2006. № 5. ;URL: https://science-education.ru/ru/article/view?id=574 (дата обращения: 11.05.2025).