В различных областях деятельности человека часто возникают задачи, в которых требуется описать реальные природные объекты и процессы, с целью изучения их свойств, структуры и законов развития, а так же их внутренних и внешних связей. Это необходимо знать для эффективного и результативного управления объектом или процессом, с одной стороны, и для наиболее точного и надежного прогнозирования, с другой стороны.
Описание реальных объектов и процессов в некоторых формальных терминах принято называть моделированием, а полученную абстракцию - моделью. Модели различают по способу их описания. Например, вербальные модели (описание текстом), математические модели (описание при помощи математического аппарата), информационные модели (знаковое или символьное описание информационных процессов). Особенностью компьютерного математического моделирования является перенесение математической модели в среду ЭВМ и переход от аналитических методов к численным методам. На практике это означает дискретизацию непрерывных переменных и функций, а также замену всех бесконечно малых и бесконечно больших величин некоторыми конечными величинами. Такое представление позволяет описать и перенести любые математические модели в среду некоторого языка программирования или в среду готовой компьютерной программы для дальнейшей работы с ней. В экономических задачах информация представляется чаще всего в табличных данных, то есть уже дискретная. Обрабатывая ее статистическими и эконометрическими методами, получаем математическую модель. В силу больших массивов данных их обработка и анализ модели не возможны без компьютерных технологий.
Составление любой модели проходит несколько этапов. На первом этапе выполняется словесная постановка задачи. Здесь определяется объект модели, начальные условия и что должно получиться в результате. Ключевая фраза: «Я хочу, чтобы...». Следующим этапом является формализация, где уясняются существенные свойства объекта и их взаимосвязь. Так как различные свойства существенны в различной степени для данной модели, то часть из них отбрасывается как несущественные. В силу последнего замечания адекватность модели реальности будет в той или иной степени приближенной.
Дальнейший этап состоит в поиске математического описания модели или в выборе из нескольких возможных. Это самый сложный и ответственный момент в моделировании, так как в модели может присутствовать достаточно большое количество связей, частей, переменных и выбор неправильного математического описания для любой из них может привести к полной или частичной неработоспособности модели в целом. Для описания взаимодействий выбираются уже известные функциональные зависимости, то есть исследованные ранее, или табличные описания - статистическую зависимость.
Последний этап состоит в программировании, то есть в перенесении полученной математической модели в среду ЭВМ. На этом этапе выбирается конкретная среда работы, или среда языка программирования, или среда существующего приложения, или то и другое. Создается, собственно, модель в виде программы или пользовательского документа. Проводятся тестирования модели с целью выяснения работоспособности и степени адекватности полученной модели. По завершению создаются инструменты работы с моделью (интерфейс).
Приведенное выше разделение моделирования на этапы носит в известной степени условный характер, так как они могут пересекаться, дополнять друг друга.
В качестве примера математического моделирования экономической задачи рассмотрим процесс роста выпуска продукции. [1]. Целью нашего моделирования будет изучение этого процесса, его графическое представление и определение прогнозных значений в некоторый момент времени.
Первый этап. Создать в среде MS Excel таблицу и диаграмму, позволяющие по заданным начальным параметрам определить уровень выпуска продукции в определенный момент времени и увидеть график его изменения во времени.
Второй этап. Для создания модели необходимо знать цену продукции, количество продукции, реализованной на момент времени t, инвестиции в производство.
Трети этап. Предположим, что цена продукции Р фиксированная. Обозначим через Q(t) количество продукции, реализованной на момент времени t. Тогда РQ(t) - доход на этот момент времени. I(t)=mPQ(t) - инвестиции в производство, 0<m<1. Если исходить из предположения о ненасыщаемости рынка или о полной реализации производимой продукции, то в результате расширения производства будет получен прирост дохода, часть которого опять будет использована для расширения выпуска продукции. Это приведет к росту скорости выпуска (акселерации), причем скорость выпуска пропорциональна увеличению инвестиций, то есть Q/=lI, где 1/l - норма акселерации. Если обозначить k=lmP, то Q/=kQ(t). Общим решение этого дифференциального уравнения будет уравнение Q=Cekt, учитывая начальные параметры, получим Q=Q0ek(t-t0) [1]. Это и есть искомая математическая модель.
Для проведения тестирования модели возьмем Q0=100 единиц товара в момент времени t=1 месяц, и k=0,1. Шаг - 1 месяц. Тогда, полученная в MS Excel [2] таблица выглядит следующим образом:
|
T |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Q |
100 |
111 |
122 |
135 |
149 |
165 |
182 |
201 |
А полученная диаграмма [2] имеет вид:
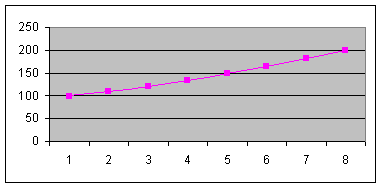
Рис. 1. Рост выпуска продукции
Следует заметить, что математические модели обладают свойством общности. Так из результатов биологических опытов следует, что процесс размножения бактерий также описывается уравнением Q/=kQ(t). Процесс радиоактивного распада подчиняется закономерности Q=Q0ek(t-t0) [1].
Завершая рассмотрение примера, отметим, что полученная модель приближенно описывает рост выпуска продукции при условии отсутствия конкуренции и пригодна для прогнозирования результата. Изменив допущение в экономическом состоянии рынка, мы получим другую модель исследуемого процесса, которая будет описывать рост выпуска продукции в условиях конкуренции [1].
СПИСОК ЛИТЕРАТУРЫ:
- Красс М. С., Чупрынов Б. П. Основы математики и ее приложения в экономическом образовании: Учеб. - 2-е изд., испр. - М.: Издательство «Дело», 2001. - 688 с.
- Леонтьев В. П. Новейшая энциклопедия персонального компьютера 2005. - М.: ОЛМА-ПРЕСС Образование, 2005. - 800 с.
Библиографическая ссылка
Миселимян Т.Л., Зацепин М.Н. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ И ПРОГРАММИРОВАНИЕ НА ЭВМ ЭКОНОМИЧЕСКИХ ЗАДАЧ // Современные проблемы науки и образования. 2007. № 5. ;URL: https://science-education.ru/ru/article/view?id=560 (дата обращения: 22.01.2026).



