В странах Европы использовали три основных типа водяных колес. Горизонтально расположенные водяные колеса с лопастями были небольшого размера и применялись, как правило, для помола зерна. Использование такого типа колеса для других целей было затруднительно из-за их малой мощности и низкого КПД (5-15 %). Большее значение в освоении энергетических ресурсов имели вертикальные колеса: подливные (нижнебойные) и черпаковые (верхнебойные). Первые имели на ободе плоские закругленные лопасти и приводились в движение потоком воды. Подливные колеса могли работать почти в любых относительно обильных потоках с умеренной скоростью воды, но наиболее эффективны они были в узких протоках. Вертикальные колеса были в 3-5 раз мощнее горизонтальных, а их КПД составлял 20-70 % в зависимости от вида [2].
При использовании верхнебойных колес вода падала сверху в черпаки, прикрепленные к ободу колеса. В этом случае колесо приводилось в движение не столько за счет удара воды, сколько под действием силы тяжести. Внизу вода выливалась из черпаков, они поднимались вверх, вновь наполнялись водой, и процесс повторялся. Такие вертикальные колеса имели коэффициент полезного действия 50-70 %. Для строительства верхнебойных колес необходимо было сооружать запруды и поднимать уровень воды в реке. Подобные построения удавалось произвести не везде, что требовало существенных расходов, кроме того, не везде создание запруд было технически возможно. Наибольшее распространение получили нижнебойные водяные колеса.
Ввиду значимости водяных колес для развития промышленного производства, проблема расчета оптимальных параметров, которые бы давали максимальную производительность, стала одной из наиболее актуальных в научных кругах. Многие инженеры и геометры - А. Паран (Antoine Parent, 1666-1716), А. Эйлер, Вандин (Du Petit-Vandin, 1713-1790), А. Малле (Jacques André Mallet, 1740-1790), Ж. Борда (Jean Charles Borda, 1733-1799), Ш. Боссю (Charles Bossut, 1730-1814), Д. Хуан (Jorge Juan), Парсо (Parcieux), Д. Смитон (John Smeaton), О. Эванс (Oliver Evans), Р. Бученан (Robertson Buchanan) - в своих теоретических и экспериментальных исследованиях предлагали свои варианты решения данной проблемы [3, 7].
При использовании нижнебойных водяных колес было замечено, что производительность колеса не является постоянной и меняется в зависимости от сезона: падение уровня воды в реке могло как снизить, так и увеличить его производительность. Помимо высоты погружения в воду важными факторами производительности нижнебойного колеса являлись его радиус, количество лопастей, их размеры, угол наклона плоскости лопасти к направлению течения и многие другие. Помимо этого, производительность водяного колеса зависела от места его сооружения - широкого русла реки или узкого канала, близкого по своей ширине к размерам водяного колеса.
Долгое время господствующей являлась теория движения водяных колес, сформулированная А. Параном в 1704 году. Суть теории заключалась в том, что наилучшая производительность колеса достигается в момент, когда тангенциальная скорость колеса втрое меньше скорости потока жидкости. Исследования ученого основывались на двух основных предположениях: воздействие напора воды на все лопасти является перпендикулярным, а каждая лопасть является независимой от других. Выводы Парана относительно производительности водяных колес в тот момент являлись общепринятыми и широко использовались инженерами, прежде всего, благодаря их простоте.
Сомнения в допустимости предпосылок Парана побудили Шарля Боссю [1], одного из ведущих экспериментаторов Франции XVIII века в области гидродинамики, исследовать проблему движения водяных колес со всей точностью и строгостью. В статье «Основы определения эффекта водяных колес, приводимых в движение напором воды» (Determination generale de l′effet des roues mues par le choc de l′eau) [5], опубликованной в сборнике Парижской академии наук за 1769 год, Шарль Боссю провел исследование с целью уточнения характеристик вертикальных нижнебойных колес, при которых их производительность была бы наибольшей. Основная идея исследования состояла в поиске импульса потока жидкости для каждой лопасти и суммировании всех частных импульсов с целью определения общего эффекта. Шарль Боссю рассматривал взаимодействие жидкости и лопасти колеса как удар. Придерживаясь существующей на тот момент теории, Боссю определил значение величины удара жидкости о поверхность как произведение площади поверхности на квадрат скорости жидкости и квадрат синуса угла, образуемого направлением потока и касательной поверхности.
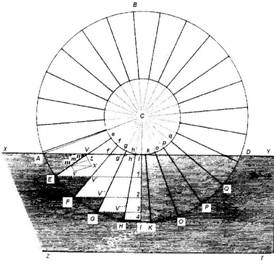
Далее Боссю внес предположения, что частицы жидкости движутся в потоке параллельно поверхности XY с одинаковой скоростью (рис. 1).
Погруженное в поток колесо AKDB с центром C имеет некое количество крыльев Ee, Ff, Gg, Hh..., направленных в радиальном направлении. На рисунке видно, что поток жидкости оказывает воздействие путем передачи импульса только части каждого крыла (элементам EV, FV′, GV″, HV′″...), при этом элементы V′f′, V″g′, V″′h′... не испытывают воздействия импульса (Боссю предполагал, что передачи импульса на этом участке не происходит).
|
|
|
Рис. 1. Вертикальное нижнебойное водяное колесо, приводимое во вращение потоком воды |
Пусть Mm элемент крыла Ee (рис. 1). My, Mx - расстояния, которые пройдет точка М крыла и частица жидкости за некоторый момент времени. Разложив расстояние Mx на два других направления My, Mz, Боссю отметил, что жидкость оказывает воздействие на Mm только в направлении Mz (поддерживая вращение колеса за счет импульса Mx). Введя обозначения всех размеров и углов (CA = a, EМ = x, Мм = dx, ![]() ACI = m,
ACI = m, ![]() ECI = p), Боссю записал значение импульса переданного жидкостью элементарной поверхности Mm по перпендикулярному направлению My, откуда вывел величину момента импульса:
ECI = p), Боссю записал значение импульса переданного жидкостью элементарной поверхности Mm по перпендикулярному направлению My, откуда вывел величину момента импульса:
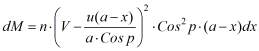 , (1)
, (1)
где V - скорость течения жидкости, u - тангенциальная скорость окружности AKDB, n - константа, характеризующая значение импульса, переданного лопасти заданного размера (определяется расчетно-опытным путем).
Прежде чем провести интегрирование, Боссю анализирует изменение величины ![]() , которая может принимать как положительное, так и отрицательное значение при любом значении x от 0 до EV. В первом случае, жидкость передает импульс вращающемуся колесу на всем протяжении лопастей, во втором, напротив, лопасти колеса подталкивают жидкость. Боссю также рассмотрел случай, когда удаленная от центра колеса часть лопасти передает импульс жидкости, в то время как другая часть приводится в движение с помощью жидкости. В этом случае величина принимает как положительное, так и отрицательное значение при изменении x от 0 до EV.
, которая может принимать как положительное, так и отрицательное значение при любом значении x от 0 до EV. В первом случае, жидкость передает импульс вращающемуся колесу на всем протяжении лопастей, во втором, напротив, лопасти колеса подталкивают жидкость. Боссю также рассмотрел случай, когда удаленная от центра колеса часть лопасти передает импульс жидкости, в то время как другая часть приводится в движение с помощью жидкости. В этом случае величина принимает как положительное, так и отрицательное значение при изменении x от 0 до EV.
Боссю остановился на рассмотрении первого случая, когда ![]() . При выполнении условия V∙Cos p = u и любом x от 0 до EV неравенство остается в силе. Например, для отношения V : u = 3 : 1 Cos p = 1/3, угол p=70,5° необходимо, чтобы величина погружения колеса в жидкость была не более чем на 2/3 от его радиуса.
. При выполнении условия V∙Cos p = u и любом x от 0 до EV неравенство остается в силе. Например, для отношения V : u = 3 : 1 Cos p = 1/3, угол p=70,5° необходимо, чтобы величина погружения колеса в жидкость была не более чем на 2/3 от его радиуса.
Проинтегрировав выражение (1) при x от 0 до EV = а ![]() (M = 0 при x = 0) и введя обозначения
(M = 0 при x = 0) и введя обозначения ![]() , u = K∙V, Боссю получил значение момента импульса жидкости на элемент EV первой лопасти колеса:
, u = K∙V, Боссю получил значение момента импульса жидкости на элемент EV первой лопасти колеса:
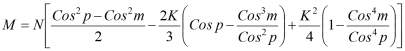 . (2)
. (2)
Аналогично записал выражения для моментов импульсов M′, M″, M″′..., действующих на элементы FV′, GV″, HV″′... других лопастей водяного колеса. При этом в уравнении угол p нужно заменить на p-q, p-2q, p-3q и т. д., а угол m на p, p-q, p-2q и т. д. Суммируя все получившиеся значения M, M′, M″, ..., MП для П+1 лопасти, на которые воздействует жидкость, Боссю получил громоздкое выражение для момента вращения колеса с заданным числом лопастей. Поскольку число лопастей конечное, то при вращении колеса угол p изменяется, значения М, M′, M″, M″′... с течением времени будут также изменяться, следовательно, их сумма может оказаться переменной. По этой причине Боссю поставил задачу отыскания силы, момент которой уравновешивал бы переменный вращающий момент колеса как функцию от t. Пусть Q - удерживающая сила, тогда справедливо выражение Q∙c∙dt = S∙N∙dt, где с - плечо силы Q, S∙N - сумма моментов, приложенных к лопастям колеса. Выражая dt в правой части равенства через dp, Боссю переписал это равенство в интегральной форме:
![]() (3)
(3)
(c увеличением dt dp уменьшается). Подставив в уравнение (3) вместо S∙N значения моментов М, M′, M″, M″′ как функций от p, Боссю его проинтегрировал. Наибольшую сложность вызвали интегрирование слагаемых следующих видов: ![]() ,
, ![]() , чему Боссю посвятил отдельную главу своей работы, предложив свою методику интегрирования указанных величин. После того, как правая часть уравнения (3) была проинтегрирована, Боссю приступил к приведению левой части уравнения. Для этого он ввел новые обозначения:
, чему Боссю посвятил отдельную главу своей работы, предложив свою методику интегрирования указанных величин. После того, как правая часть уравнения (3) была проинтегрирована, Боссю приступил к приведению левой части уравнения. Для этого он ввел новые обозначения: ![]() , где Q′ - средняя сила, произведенная вращающимся на угол q колесом за время t. После проведения всех преобразований и упрощений, Боссю получил уравнение вида
, где Q′ - средняя сила, произведенная вращающимся на угол q колесом за время t. После проведения всех преобразований и упрощений, Боссю получил уравнение вида ![]() , где А, В, С - константы, u - скорость колеса, v - скорость потока.
, где А, В, С - константы, u - скорость колеса, v - скорость потока.
Заключительным этапом первой части исследования стало нахождение скорости колеса, при которой производительность колеса была бы наибольшей. Для этого Боссю отыскал дифференциал уравнения и приравнял его нулю, получив выражение для искомой величины u: ![]() .
.
Таким образом, попытка Боссю провести расчет производительности водяного колеса, учитывая все параметры, привела к чрезмерному усложнению уравнения, и как следствие, невозможности проведения его анализа и поиска оптимальных параметров, записанных в аналитическом виде, при которых производительность была бы максимальной. Шарль Боссю пишет: «Непросто найти с помощью нашей основной формулы оптимальное количество лопастей колеса, вращающегося с конечной скоростью относительно потока, поскольку выражение для максимальной производительности чрезвычайно сложное и почти не поддающееся трактовке» [6, 1 том, с.525].
Отыскать оптимальные параметры нижнебойного водяного колеса Шарлю Боссю удалось, проведя дополнительные экспериментальные исследования, в 1770 году. В экспериментах Боссю использовал три модели водяных колес: два нижнебойных колеса (диаметром 0,97 и 1,03 м соответственно, шириной 0,14 м), используемых в узком и широком канале (шириной 3,9-4,2 м), а также верхнебойное колесо (диаметром 0,97 м, шириной 0,14 м).
На нижнебойных колесах Боссю проверял эффекты, производимые изменением числа лопастей, их наклоном, скоростью вращения колеса, а также влиянием ширины канала на производительность колеса. Для верхнебойных колес он изучал влияние скорости вращения колеса на его производительность.
Эксперименты Боссю по влиянию числа лопастей и их наклона были более значимыми, чем эксперименты его предшественников Парсо, Вандина. Боссю, в частности, показал, что число лопастей имеет свое оптимальное значение для наибольшей производительности. Эксперименты Боссю по определению наклона лопастей проводились как в узких каналах, так и на открытом течении. Для открытого течения он обнаружил, что увеличение наклона лопастей до определенного угла, зависящего от уровня погружения колеса и скорости потока, немного увеличивает его производительность. При дальнейшем увеличении угла производительность начинает снижаться. Для стесненного канала Боссю обнаружил, что традиционные радиальные лопасти давали результат немного лучше, чем лопасти наклоненные [7].
Эксперименты Боссю по поиску оптимальной скорости вращения нижнебойных и верхнебойных колес дополнили работы его предшественников. Для нижнебойных колес он использовал как стесненный, так и широкий канал. В обоих случаях оптимум скорости был близко к 0,4V (V - скорость обода колеса), подтвердив работу Смитона. Его эксперименты с верхнебойным колесом показали, что чем медленнее колесо движется, тем больше его производительность для заданного объема воды и высоты падения.
Основные результаты экспериментальных исследований были опубликованы Боссю в «Теоретическом и экспериментальном трактате по гидродинамике» [6, 2 том, c. 411-427].
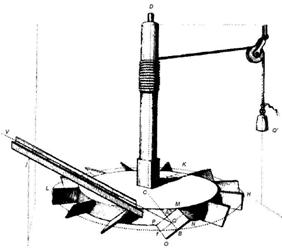
Заключительная часть теоретического исследования Боссю была посвящена описанию движения водяного колеса, установленного в горизонтальной плоскости. Вращение колеса происходит под действием струи жидкости, падающей на лопатки колеса с некоторой высоты (рис. 2).
|
|
|
Рис. 2. Горизонтальное водяное колесо, приводимое во вращение импульсом струи воды |
Боссю провел поиск параметров оптимального водяного колеса с меньшей строгостью, чем исследование движение вертикально расположенного колеса, чтобы получить более наглядную зависимость, применимую без особого труда к практическим задачам.
Импульс струи жидкости создает некоторый вращающий момент колеса, который уравновешивается моментом некоторой силы Q′ (рис. 2). Боссю поставил задачу отыскания оптимального размещения лопаток колеса (угла наклона ![]() LQe = p), а также скорости его вращения u, при которых отдача колеса была бы максимальной.
LQe = p), а также скорости его вращения u, при которых отдача колеса была бы максимальной.
Проведя все необходимые расчеты, Боссю получил оптимальную скорость вращения колеса ![]() , где V - скорость потока струи воды, при этом наибольшая производительность колеса становится равна весу воды поднятой на
, где V - скорость потока струи воды, при этом наибольшая производительность колеса становится равна весу воды поднятой на ![]() высоты падающей струи жидкости, вращающей колесо.
высоты падающей струи жидкости, вращающей колесо.
В целом, результаты, полученные Шарлем Боссю для горизонтальных водяных колес, совпали с результатами практических исследований его предшественников и современников и могли быть использованы для оценки производительности колес на этапе их сооружения [7].
Водяное колесо как основной «двигатель» промышленной революции XVII-XVIII вв. нуждалось в постоянном совершенствовании. Постоянное улучшение параметров водяного колеса, увеличение его мощности и КПД не могло быть произведено исключительно опытным путем, без опоры на теоретическую основу и построения математической модели. Именно Шарль Боссю - один из немногих ученых своего времени, осознавая значимость для науки сочетания обоих подходов, теоретического и экспериментального, осуществил расчеты основных оптимальных параметров водяных колес: вертикальных и горизонтальных. На основе своих теоретических исследований провел серию экспериментов, восполнив недостающие знания по исследуемому вопросу и проведя их теоретическое обоснование.
Рекомендации Шарля Боссю позволили увеличить эффективность нижнебойных водяных колес, используемых на реках и каналах Франции. Его экспериментальные результаты подтвердили основные теоретические положения и расширили представление о влиянии ряда параметров на производительность водяных колес, принцип сооружения которых и ныне используется в гидрогенерации.
Рецензенты:
Яковлев В. И., д.ф.-м.н., профессор, декан механико-математического факультета ФГБОУ ВПО Пермского государственного национального исследовательского университета, г. Пермь.
Пенский О. Г., д.т.н., профессор кафедры «Процессов управления и информационной безопасности» ФГБОУ ВПО Пермского государственного национального исследовательского университета, г. Пермь.
Библиографическая ссылка
Левковский П.Е. ПОИСК ОПТИМАЛЬНОЙ КОНСТРУКЦИИ ВОДЯНЫХ КОЛЕС В РАБОТАХ ШАРЛЯ БОССЮ // Современные проблемы науки и образования. 2012. № 1. ;URL: https://science-education.ru/ru/article/view?id=5596 (дата обращения: 19.02.2026).