Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Токарев К.Е. 1 Токарева Ю.М. 2

---

1 ФГБОУ ВПО «Волгоградская государственная сельскохозяйственная академия», Волгоград

2 ГБОУ ВПО «Волгоградский государственный медицинский университет Минздравсоцразвития России», Волгоград

В статье представлена методика применения факторного анализа для выявления критериев, влияющих на формирование удовлетворенности пациентов качеством медицинских услуг. Для исследования были созданы две группы респондентов: контрольная и экспериментальная. Обработку данных опроса необходимо основывать на составлении таблиц сопряженности. Каждому ответу присваивается числовая характеристика, формулируется статистическая и нулевая гипотеза, а также назначаются уровень значимости и доверительная вероятность. Применяя «нормальный закон» Гаусса, был вычислен интегральный показатель, который подтвердил, что материально-техническое оснащение ЛПУ оказывает опосредованное влияние на оценку качества медицинских услуг пациентом. Другие факторы, определяющие формирование удовлетворенности от взаимодействия с медицинской подсистемой, могут быть обнаружены в результате проведения рангового анализа критериев всей выборочной совокупности. Данная методика является универсальной и может быть использована в системе здравоохранения при сопоставлении различных антагонистических групп факторов.

Статья в формате PDF

95 KB

статистическая гипотеза.

таблица сопряженности

ранжирование

качество медицинских услуг

1. Бююль А., Цёфель П. SPSS: Искусство обработки информации. Анализ статистических данных и восстановление скрытых закономерностей. – СПб.: ООО «ДиаСофтЮП», 2002. – 603 с.

2. Математические методы в социологии. Анализ данных и логика вывода в эмпирическом исследовании: учеб. пособие для вузов / Р. Л. Агабекян, М. М. Кириченко, С. В. Усатиков. – Ростов н/Д: Феникс, 2005. –192 с.

3. Токарев К. Е. Оценка эффективности оказания медицинских услуг в условиях необходимости повышения их качества // «Бизнес. Образование. Право». Вестник института бизнеса. – 2011. – № 3.

4. Токарева Ю. М., Чижова В. М. Применение факторного анализа для оценки качества медицинской помощи // Вестник Волгоградского государственного медицинского университета. – 2009. – № 3. – С.96-99.

5. Факторный, дискриминантный и кластерный анализ: Пер. с англ./Дж.-О. Ким, Ч. У. Мьюллер, У. Р. Клекка и др.; Под ред. И. С. Енюкова. – М.: Финансы и статистика, 1989. – 215 с.

Таблица 1.  Пример двухмерной таблицы сопряженности: «Удовлетворены ли Вы качеством медицинских услуг?»

Таблицы сопряженности могут также представлять взаимосвязь трех и более переменных. Однако группировка дынных, более чем по трем признакам, сложна и потому может рассматриваться на начальной стадии, с целью выявления ненужной информации и выделения  наиболее значимых закономерностей. Таблицы сопряженности демонстрируют определенную закономерность в развитии двух и  более признаков, либо ее отсутствие. Подобные исследования также обнаруживают влияние различных факторов на исследуемый объект. Согласно общепринятому определению, факторный анализ - (от лат. factor - действующий, производящий и греч. analysis - разложение, расчленение) - метод многомерной математической статистики, применяемый при исследовании статистически связанных признаков с целью выявления определенного числа скрытых от непосредственного наблюдения факторов. Задача факторного анализа состоит в замене набора параметров меньшим числом некоторых категорий («факторов»), являющихся линейной комбинацией исходных параметров. Удовлетворительным решением служит такая система факторов, которая достаточно адекватно передает информацию, имеющуюся в наборе параметров. Таким образом, главная цель факторного анализа - сжатие информации, экономное описание.

Одна и та же матрица корреляций может быть факторизована бесчисленным количеством способов. Возможно, именно неосведомленность об этом факте послужила причиной бурных дискуссий о «правильном», «наилучшем» или «инвариантном» решении для данного набора параметров. Раз возможно бесконечное число одинаково «правильных»  решений, то естественно возникает вопрос: как произвести выбор? Выбор типа нужного факторного решения производится на основании двух принципов: 1) статистической простоты; 2) содержательного социологического смысла (если речь идет о социологии). В свою очередь, каждый из этих принципов может быть по-разному интерпретирован; доказательством тому служит неоднозначное их применение различными школами факторного анализа.

Если иметь в виду чисто статистический поход, то естественно заменить исходный набор параметров несколькими факторами, определяемыми последовательно и таким образом, чтобы каждый из последующих факторов «отбирал на себя» максимум из оставшейся суммарной дисперсии параметров. Этот статистический оптимальный подход и соответствующий метод главных осей был впервые предложен Пирсоном в начале столетия и досконально разработан Хотеллингом в 1930-х годах. Алгоритмы метода главных компонентов весьма эффективны с точки зрения результатов, но очень трудоемки: вычислить вручную главные компоненты для матрицы 10-го и более высокого порядка практически невозможно. В последние годы, однако, эта трудность была преодолена благодаря быстродействующим ЭВМ.

Другим методом, основанным на статистическом подходе, является центроидный метод. Этот метод был введен в употребление как вычислительный паллиатив (мера, не обеспечивающая полного, коренного решения задачи) после того, как стала ясна практическая нереализуемость метода главных факторов. Это означает, что цетроидный метод позволяет достаточно легко из многих систем координат выбрать такую, которая в смысле распределения дисперсии приближается к оптимальной системе.

В поисках содержательно значимых методов были созданы различные теории в надежде найти такой единственный метод, который был бы одинаково хорош при исследовании любых параметров.

Методы факторного анализа нашли применение, главным образом, в социологии. Решение, полученное методами факторного анализа, может послужить основой при формулировании некоторой научной гипотезы; возможно и обратное: методами факторного анализа находится подтверждение существующей гипотезы.

В начале статьи мы приводили пример темы исследования в социологии медицины. Рассмотрим его как образец сравнения двух выборочных совокупностей. Напомним, что речь шла о выявлении степени влияния материально-технического оснащения стационара на формирование удовлетворенности пациентов качеством медицинских услуг. Для исследования нужны однородные объекты, разделенные на две группы. В нашем случае респонденты - это пациенты одного стационара, опрошенные до и после инновационного материально-технического оснащения. Для каждого объекта регистрируется его некоторая числовая характеристика (Табл. 2).

Прежде чем воспринимать эти числа как факт и основание для вывода, следует помнить о случайности отличий и отсутствии значимых различий в числах этих двух выборок. В связи с чем, придется выдвинуть статистическую гипотезу об отсутствии различий или нулевую гипотезу.

Назначим уровень значимости ɑ, как показатель вероятности ошибочно отвергнуть нулевую гипотезу, или p = 1- ɑ - доверительную вероятность. Например, ɑ = 0,003 (или 0,3 %) означает риск ошибиться в 3 случаях из 1000. Гипотеза отвергается, если в эксперименте наблюдается явление, чья вероятность по гипотезе мала (равна ɑ).

Таблица 2.  Удовлетворенность пациентов качеством медицинских услуг

Целью нашего исследования является выявление степени влияния на удовлетворенность пациента от взаимодействия с медицинской подсистемой материально-технического оснащения. Сформированы экспериментальная и контрольная группы. В экспериментальную группу вошли пациенты стационара, проходящие лечение после обновления материально-технической базы. Контрольная группа - респонденты, опрошенные нами до переоснащения ЛПУ. Цель анализа - определить эффективность проведенной работы. Представители двух групп отвечали на вопросы анкеты, на основании которых рассчитывался интегральный показатель зависимости исследуемых факторов.

Упорядочим все полученные оценки, присваивая им ранги по возрастанию. Под рангом понимается порядковый номер числа. Если несколько чисел совпадают по величине, то каждому из них присваивается ранг, равный среднему арифметическому их номеров (Табл. 3).

Таблица 3.  Ранжирование оценок пациентами качества медицинских услуг

Пусть в первой выборке N1 чисел, во второй N2 чисел. Обозначим сумму рангов первой выборки R1, R2 - сумма рангов второй выборки. При больших объемах выборки N1 и N2 (практически N1›8 и N2›8) по центральной предельной теореме случайные числа R1 и R2 подчиняются «нормальному закону», который был впервые обнаружен в XIX веке в применении к теории ошибок измерения Лапласом и Гауссом.

Поэтому первоначально необходимо вычислить числа W1 (1.1), W2 (1.2).

                               (1.1)

                    (1.2)

Затем найти среди них минимальное значение, обозначим его W и вычислим число Z 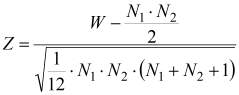(2).

                      (2)

То можно доказать, что оно подчиняется Z - закону Гаусса. Для закона Z свойственно правило «трех ợ», т.е. можно сказать, что при ợ = 0,003 величина |Z|≥3. Следовательно,  нулевая гипотеза отклоняется при ợ = 0,003, если |Z|≥3; или при ợ = 0,05, если |Z|≥2; или при  ợ = 0,3, если |Z|›1. В противном случае числа из выборок не дают основания утверждать, что способ обработки оказывает вообще какое-либо действие. При других уровнях значимости ɑ величину критического значения |Z| необходимо брать из таблиц распределения Гаусса в статистических справочниках.

В нашем случае суммы рангов: R₁=129,5 и  R₂= 123,5. Заметим, что N₁=12, N₂=10. Получим:

                           (3.1.)

                                 (3.2)

минимальное из которых - W=51,5.

Вычислим число Z:

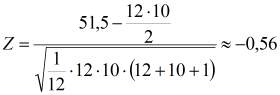                         (4)

Следовательно,  |Z|= 0,56 и нулевая гипотеза о полной бесполезности проведенной работы не может быть отброшена ни при ɑ=0,003, ни при ɑ=0,05, ни при ɑ=0,3, так как полученное значение меньше и 3, и 2, и 1. Но эти исследования не дают исследователю содержательного ответа о причинах, обусловивших отсутствие различий.

Материально-техническое оснащение ЛПУ оказывает опосредованное влияние на оценку качества медицинских услуг пациентом. Такой вывод позволяет сделать проведенное исследование с применением метода ранжирования в двух выборочных совокупностях. Однако исследование не определяет те факторы, которые формируют удовлетворенность пациента. Подобную информацию можно получить в результате рангового анализа оценок респондентов в экспериментальной и контрольной группах по следующим параметрам: взаимоотношения с лечащим врачом, профессионализм медицинского персонала, бесплатность медицинских услуг и т. д.

Рецензенты

Рогачев А. Ф., д.т.н., профессор, заведующий кафедрой «Информатика, ТМ и ОНИ» ФГБОУ ВПО Волгоградская государственная сельскохозяйственная академия, г. Волгоград.

Козенко З. Н., д.э.н., профессор кафедры «Экономическая теория и СКК», ФГБОУ ВПО Волгоградская государственная сельскохозяйственная академия, г. Волгоград.

Библиографическая ссылка