Рассмотрим математическую модель на примере энергетического привода магистрального нефтеперекачивающего насоса НМ 10000-210. Обычно это синхронный трехфазный электродвигатель СТД-8000 мощностью 8 МВт. В процессе его эксплуатации обычно возникает и развивается неуравновешенность ротора. Неисправность такого вида устраняют путем установки небольших уравновешивающих грузов в определенные углы балансировочных плоскостей ротора. Далее приводится модель, которая позволяет провести теоретический расчет состояния агрегата и предотвратить длительную остановку производственного процесса.
Во время эксплуатации несбалансированного ротора в нем возникает центробежная сила, зависящая от неравномерности распределения масс относительно оси вращения и частоты его вращения:
![]() , (1)
, (1)
где m - величина дисбаланса, кг; r - расстояние от оси ротора, на котором расположен дисбаланс, м; n - частота вращения ротора, c-1.
Она вызывает вынужденные колебания конструктивных составляющих электродвигателя в поперечном сечении, которые могут быть описаны неоднородным дифференциальным уравнением второго порядка:
![]() , (2)
, (2)
где S - виброперемещение, м; ![]() - время, c; h - коэффициент сопротивления среды, c-1; ω0 - собственная частота колебаний рассматриваемой системы, c-1;
- время, c; h - коэффициент сопротивления среды, c-1; ω0 - собственная частота колебаний рассматриваемой системы, c-1; ![]() - амплитуда вынуждающей силы;
- амплитуда вынуждающей силы; ![]() - центробежная сила, вызывающая вибрацию, H; M - масса системы участвующей в колебаниях, кг; ωn - частота вынуждающей силы, т.е. частота вращения ротора, c-1; φ - фазовый сдвиг возникающего колебания относительно фазы возмущающей силы.
- центробежная сила, вызывающая вибрацию, H; M - масса системы участвующей в колебаниях, кг; ωn - частота вынуждающей силы, т.е. частота вращения ротора, c-1; φ - фазовый сдвиг возникающего колебания относительно фазы возмущающей силы.
Общее решение уравнения (2) представляет собой сумму общего решения однородного уравнения и частного решения неоднородного:
![]() (3)
(3)
Первое слагаемое соответствует затухающим колебаниям в зависимости от демпфирующих сил и жесткости системы:
![]() . (4)
. (4)
В граничном случае ![]() и случае большого сопротивления среды
и случае большого сопротивления среды ![]() происходит апериодическое движение системы. Наличие небольших сил сопротивления
происходит апериодическое движение системы. Наличие небольших сил сопротивления ![]() вызывает постепенное уменьшение амплитуды колебаний и их затухание. Насколько быстро происходит затухание, определяется величиной
вызывает постепенное уменьшение амплитуды колебаний и их затухание. Насколько быстро происходит затухание, определяется величиной ![]() , называемой декрементом (уменьшением) колебаний. Здесь T1 - период затухающих колебаний. Таким образом, определять движение системы через некоторое время будут чисто вынужденные колебания, описываемые вторым слагаемым:
, называемой декрементом (уменьшением) колебаний. Здесь T1 - период затухающих колебаний. Таким образом, определять движение системы через некоторое время будут чисто вынужденные колебания, описываемые вторым слагаемым:
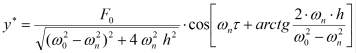 . (5)
. (5)
В случае вынужденных колебаний, когда ![]() , общее решение состоит из двух групп слагаемых: так называемых сопровождающих колебаний, которые происходят с почти собственной частотой ω0, и чисто вынужденных колебаний, происходящих с частотой ωn вынуждающей силы. Для установления зависимости виброскорости точек ротора от вынуждающей силы продифференцируем по времени уравнение (3) и, упростив его, получим:
, общее решение состоит из двух групп слагаемых: так называемых сопровождающих колебаний, которые происходят с почти собственной частотой ω0, и чисто вынужденных колебаний, происходящих с частотой ωn вынуждающей силы. Для установления зависимости виброскорости точек ротора от вынуждающей силы продифференцируем по времени уравнение (3) и, упростив его, получим:
![]()
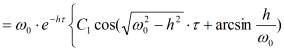
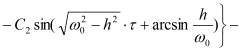
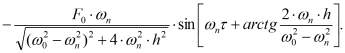 (6)
(6)
В поперечной к оси ротора плоскости происходят синхронные колебания точек ротора в вертикальном и горизонтально-поперечном направлении, которые можно описывать уравнением с комплексными функциями амплитуды A и фазы φ в одном из видов записи:
![]() , (7)
, (7)
где A амплитуда колебаний, измеряемая в мм или мкм, φ - фаза колебаний в градусах или радианах, ![]() мнимая единица. Графически такие колебания можно изображать в виде векторов комплексной плоскости, где действительную часть Ax комплексной величины откладывают вдоль оси абсцисс, а мнимую Ay - вдоль оси ординат. Такой подход позволяет довольно легко осуществлять и экспериментальный контроль над вибрацией ротора.
мнимая единица. Графически такие колебания можно изображать в виде векторов комплексной плоскости, где действительную часть Ax комплексной величины откладывают вдоль оси абсцисс, а мнимую Ay - вдоль оси ординат. Такой подход позволяет довольно легко осуществлять и экспериментальный контроль над вибрацией ротора.
Ротор электродвигателя - протяженное тело, замер вибросигналов обычно осуществляют с помощью датчиков, расположенных в поперечных сечениях на подшипниках. Расстояние между передним и задним подшипниками нашего ротора составляет 3,5 метра. На этом расстоянии в процессе эксплуатации ротора могут случаться различные повреждения, изменения, деформации, как вследствие сил электромагнитного, так и механического происхождения. Все это будет влиять на характеристики вибросигнала, снимаемые с датчиков на переднем и заднем подшипниках. По данным, получаемым с двух подшипников, можно диагностировать состояние агрегата и производить своевременную балансировку его ротора, не доводя до аварийных ситуаций.
Так как при установившемся режиме работы электродвигателя параметры, входящие в уравнения вибрации, есть квазистационарные величины, то зависимость скорости вибрации энергопривода от силы, ее вызывающей, представим в виде некоторой линейной модели:
![]() , (8)
, (8)
причем будем полагать коэффициенты p и q комплексными величинами.
В данной модели комплексность коэффициента p, на наш взгляд, отражает факт, что действительная его часть позволяет оценить величину балансировочной массы, а мнимая - угол, под которым она должна быть установлена в балансировочной плоскости. Казалось бы, что значение параметра q для заднего и переднего подшипников в расчетах можно считать нулевыми, т.к. при отсутствии возмущающей силы должна отсутствовать и вибрация. Но при существующих методах балансировки механических систем такой эффект маловероятен.
При изучении данных вибородиагностических обследований парка насосных агрегатов нефтеперекачивающих станций Тюменской области в 2008-2009 годах по балансировке роторов, снятых на синхронных трехфазных электродвигателях СТД-8000 с применением зависимости (8), были получены следующие теоретические значения коэффициентов (рис. 1):
![]() и
и ![]() для заднего подшипника;
для заднего подшипника;
![]() и
и ![]() для переднего подшипника.
для переднего подшипника.
На рисунках представлены значения коэффициентов k и b, извлеченные из обработки экспериментальных данных методом наименьших квадратов, и среднеквадратичные отклонения R2 от линейной зависимости ![]() :
:
![]() и
и ![]() для заднего подшипника;
для заднего подшипника;
![]() и
и ![]() для переднего подшипника.
для переднего подшипника.
Как видно из диаграмм, математическая модель (8) вибросостояния ротора электродвигателя обеспечивает приемлемый уровень соответствия развития событий и может быть использована для прогнозирования технического состояния агрегата, имеющего аналогичную неисправность. Расхождение экспериментальной и теоретической кривых вполне закономерно. Чем меньшей возбуждающей силе соответствует значение виброскорости ротора, тем меньшей массой можно устранить возникший в нем дисбаланс.
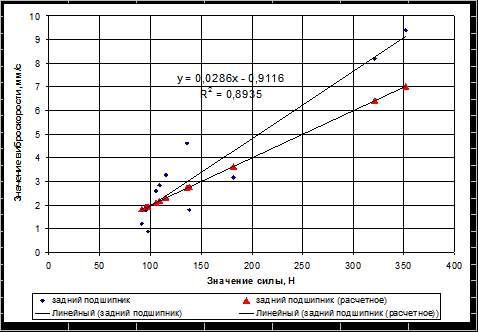
(а)

(б)
Рис. 1. Зависимость величины виброскорости V заднего - (а) и переднего - (б) подшипников электродвигателя от расчетных значений центробежной силы (![]() ).
).
Увеличение расхождения между теоретической и экспериментальной кривыми довольно легко объяснить. Теоретическая зависимость дает только максимально возможные значения виброскорости за счет разбалансировки ротора. А в экспериментальную зависимость вносят вклад и другие возможные неисправности ротора, как то: нарушение соосности, изменение жесткости и т.д. Большое отличие теоретических q и экспериментальных b параметров только подтверждает факт, что при современном техническом уровне балансировки оборудования достичь теоретических значений этого параметра невозможно.
При балансировке на собственных подшипниках исследуемых роторов оценивалась величина балансировочной массы, которую необходимо добавить в соответствующую плоскость ротора с помощью теоретической зависимости. Окончательный подбор массы производился с помощью дополнительных вибродиагностических измерений. По стандартной методике построения векторных диаграмм виброскоростей переднего и заднего подшипников определялись углы, в которых эта масса должна быть установлена. В рассматриваемых нами обследованиях были применены одноплоскостная либо двухплоскостная балансировка симметричного жесткого ротора в зависимости от наличия только статической, динамической либо сразу двух видов разбалансировки.
Предложенная математическая модель позволяет проводить теоретический расчет и предсказание состояния энергопривода. А также повышать качество работ по балансировке агрегата и уменьшать стоимость работ по восстановлению работоспособного состояния ротора.
Рецензенты:
Земенков Ю.Д., д.т.н., профессор, зав. кафедрой «Транспорт углеводородных ресурсов», ФГБОУ «Тюменский государственный нефтегазовый университет», г. Тюмень.
Шабаров А.Б., д.т.н., профессор, зав. кафедрой механики многофазных систем, ФГБОУ ВПО «ТюмГУ», г. Тюмень.
Библиографическая ссылка
Захаренко С.О., Лободенко Е.И. МОДЕЛИРОВАНИЕ ВИБРОСОСТОЯНИЯ ЭНЕРГОПРИВОДОВ // Современные проблемы науки и образования. 2012. № 1. ;URL: https://science-education.ru/ru/article/view?id=5555 (дата обращения: 19.02.2026).



