Для качественной подготовки судоводителей на специализированных тренажерах необходимы основанные на уравнениях движения судна математические модели, адекватно отражающие процессы динамического взаимодействия судового корпуса с окружающей его водой и с движительно-рулевым комплексом (ДРК). Стоит отметить, что задачи математического моделирования работы ДРК при маневрировании судна остаются до сих пор нерешёнными.
Разработка метода
Уравнение продольных сил, действующих на судно при установившемся циркуляционном движении, имеет следующий вид [5]:
![]()
где m - масса судна;
![]() - линейная скорость центра масс (ЦМ) судна;
- линейная скорость центра масс (ЦМ) судна;
ω - угловая скорость вращения судна относительно вертикальной оси , проходящей через его ЦМ;
β - угол дрейфа судна;
Xp - продольная составляющая силы, развиваемой движительно-рулевым комплексом (ДРК);
XГ - продольная составляющая сопротивления воды движению корпуса судна.
Сила Xp, которую развивает ДРК, состоящий из открытого гребного винта и установленного за ним руля, может быть представлена выражением:
![]() (2)
(2)
Здесь ![]() - число винтов;
- число винтов;
![]() - полезная тяга движителя;
- полезная тяга движителя;
![]() - угол перекладки руля;
- угол перекладки руля;
P - упор движителя;
![]() - коэффициент засасывания.
- коэффициент засасывания.
Коэффициент засасывания ![]() может считаться величиной постоянной, зависящей лишь от геометрических характеристик кормовой оконечности судового корпуса в районе выхода гребного вала. Поэтому при известном значении сопротивления воды прямолинейному движению судна коэффициент засасывания может быть подсчитан по формуле:
может считаться величиной постоянной, зависящей лишь от геометрических характеристик кормовой оконечности судового корпуса в районе выхода гребного вала. Поэтому при известном значении сопротивления воды прямолинейному движению судна коэффициент засасывания может быть подсчитан по формуле:
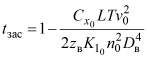
где ![]() - коэффициент общего сопротивления воды прямолинейному движению судна;
- коэффициент общего сопротивления воды прямолинейному движению судна;
L, T - расчётные длина и осадка судна;
![]() - скорость прямолинейного движения судна, соответствующая частоте вращения винтов n0;
- скорость прямолинейного движения судна, соответствующая частоте вращения винтов n0;
![]() - коэффициент упора винта при относительной поступи
- коэффициент упора винта при относительной поступи
![]()
![]() - диаметр винта;
- диаметр винта;
![]() - расчётное значение коэффициента попутного потока, определяемое по данным работы [1].
- расчётное значение коэффициента попутного потока, определяемое по данным работы [1].
Следовательно, полезная тяга винта в зависимости от его относительной поступи ![]() может быть представлена в виде
может быть представлена в виде
![]() (3)
(3)
В выражении (3) обозначено:
![]() - коэффициенты аппроксимации, получаемые при обработке диаграмм для расчёта открытых гребных винтов [2];
- коэффициенты аппроксимации, получаемые при обработке диаграмм для расчёта открытых гребных винтов [2];
ρ - массовая плотность воды;
n - частота вращения винта.
Относительная поступь гребного винта ![]() рассчитывается следующим образом:
рассчитывается следующим образом:
![]() (4)
(4)
Здесь ![]() - продольная составляющая вектора линейной скорости судна.
- продольная составляющая вектора линейной скорости судна.
Сила сопротивления воды продольному движению судна может быть подсчитана по выражению:
![]() (5)
(5)
где ![]() - коэффициент сопротивления воды продольному перемещению корпуса судна.
- коэффициент сопротивления воды продольному перемещению корпуса судна.
Для приближённых вычислений можно положить [5]
![]() (6)
(6)
В формуле (6) обозначено:
δ - коэффициент полноты водоизмещения судна;
B - ширина судна;
R - радиус установившейся циркуляции при перекладке руля на угол .
![]() - коэффициент, подсчитываемый по данным работы [5].
- коэффициент, подсчитываемый по данным работы [5].
С учётом изложенного уравнение (1) представим в виде
![]()
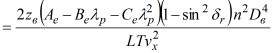 (7)
(7)
Введём следующие обозначения:
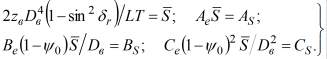 (8)
(8)
Подставив выражения (8) в равенство (7), получим:
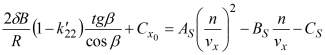 (9)
(9)
откуда
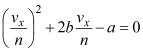 (10)
(10)
В уравнении (10) обозначено:
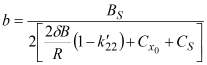
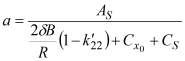
Выражение (10) позволяет найти соотношение между продольной составляющей скорости судна на установившейся циркуляции и частотой вращения винтов, то есть
![]() (11)
(11)
Для определения частоты вращения винтов воспользуемся полученным в [5] уравнением моментов:
![]() (12)
(12)
Здесь ![]() - крутящий момент на валу гребного винта;
- крутящий момент на валу гребного винта;
![]() - момент сопротивления жидкости вращению винта;
- момент сопротивления жидкости вращению винта;
![]() - коэффициент, учитывающий отношение площади диска винта, перекрываемой рулём при гипотетической перекладке последнего на 90°, ко всей площади диска.
- коэффициент, учитывающий отношение площади диска винта, перекрываемой рулём при гипотетической перекладке последнего на 90°, ко всей площади диска.
Момент сопротивления Mc определяется известной формулой
![]() (13)
(13)
а коэффициент момента K2 с использованием диаграмм для расчёта открытых гребных винтов [2] может быть представлен в виде
![]() (14)
(14)
Для приближённых расчётов крутящий момент ![]() с учётом работы регулятора частоты вращения винта может быть представлен следующим образом:
с учётом работы регулятора частоты вращения винта может быть представлен следующим образом:
![]() (15)
(15)
где
![]() ;
; ![]()
Очевидно, что
![]() (16)
(16)
Подставив формулы (13)-(15) в уравнение (12), получим:
![]() (17)
(17)
где
![]()
![]()
![]()
Таким образом, выражения (11) и (17) позволяют определить значения продольной составляющей скорости судна и частоты вращения винтов на установившейся циркуляции.
Проверка корректности метода
Для проверки корректности предлагаемой методики были выполнены расчёты относительной скорости
![]()
и параметров работы винтового движителя для десяти судов, оборудованных различными ДРК: три с открытыми винтами и расположенными за ними рулями; два с винтами в направляющей насадке и расположенными за ними рулями; три с винтами в поворотной насадке и два с винтами в поворотной насадке со стабилизатором. При этом использовались результаты натурных циркуляционных испытаний [4].
Полученные значения относительной скорости ![]() точками показаны на рис. 1. Для сравнительной оценки результатов расчёта с результатами, получающимися путём вычислений по эмпирическим формулам, на рис. 1. представлены кривые вида
точками показаны на рис. 1. Для сравнительной оценки результатов расчёта с результатами, получающимися путём вычислений по эмпирическим формулам, на рис. 1. представлены кривые вида ![]() , где
, где ![]() , построенные с использованием следующих выражений [3]:
, построенные с использованием следующих выражений [3]:
1) по Г.А. Фирсову
|
|
(18) |
2) по Р.Я. Першицу
|
|
(19) |
3) по А.М. Басину
|
|
(20) |
4) по А.Д. Гофману и В.И. Когану
|
|
(21) |
5) по О.И. Гордееву и В.Г. Павленко
|
|
(22) |
6) по Ю.М. Мастушкину
|
|
(23) |
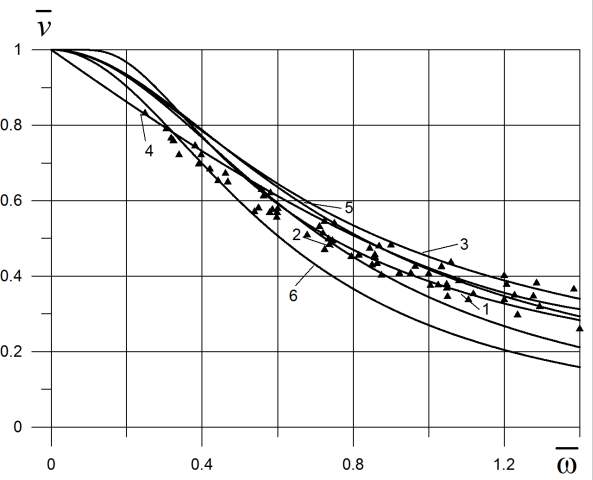
Рис. 1. Результаты расчётов падения линейной скорости на циркуляции.
Вывод
Удовлетворительная сходимость расчётных и экспериментальных значений величины позволяет сделать вывод о том, что предлагаемый способ аналитического определения скорости судна на установившейся циркуляции достаточно корректен. Следует отметить, что инерционность гребного винта пренебрежимо мала по сравнению с инерционностью судна. Поэтому в любой момент времени параметры работы винтового движителя будут определяться мгновенными значениями характеристик движения судна. Следовательно, разработанный автором метод может быть использован для моделирования работы винтового движителя при неустановившемся криволинейном движении судна.
Рецензенты:
Клементьев А.Н., д.т.н., профессор, зав. кафедрой судовождения и безопасности судоходства ФБОУ ВПО «Волжская государственная академия водного транспорта», г. Нижний Новгород.
Тихонов В.И., д.т.н., профессор кафедры судовождения и безопасности судоходства ФБОУ ВПО «Волжская государственная академия водного транспорта», г. Нижний Новгород.
Библиографическая ссылка
Бажанкин Ю.В. МЕТОД АНАЛИТИЧЕСКОГО ОПРЕДЕЛЕНИЯ СКОРОСТИ СУДНА НА УСТАНОВИВШЕЙСЯ ЦИРКУЛЯЦИИ // Современные проблемы науки и образования. 2012. № 1. ;URL: https://science-education.ru/ru/article/view?id=5550 (дата обращения: 19.02.2026).



