Вопросам расчета восстанавливаемых систем с наличием комплекта запасных элементов уделяется повышенное внимание специалистов. Данный вопрос начал обсуждаться в 60-е годы XX столетия. Впервые понятие запасного элемента было введено в работе [7] в 1964 году. И можно смело отметить, что актуальность данного вопроса не потеряна до сих пор. Достаточно указать работы [1-3; 5; 6], опубликованные уже в XXI веке. Мы не будем здесь останавливаться на обзоре литературы по данной теме. Отошлем читателя к работам [5; 6], в которых выполнен достаточно полный обзор литературы как в историческом плане, так и в плане описания моделей, применяемых для решения задачи расчета надежности систем с учетом запасных элементов (ЗИП) и оптимизации состава ЗИП.
Постановка задачи
В данной работе рассмотрим вопросы формирования комплектов запасных изделий и приборов (ЗИП) в некоторых специфических условиях функционирования. Рассмотрим общую схему использования запасных элементов, в том числе будем рассматривать случай, когда эти элементы находятся под нагрузкой. Практикой эксплуатации установлено, что если вместо отказавшего элемента включается в работу объект, который до того находился на хранении, то есть имел место холодный резерв, то в момент установки объекта в систему он подвергается стрессовым воздействиям, так как в момент его включения в работу на него действуют переходные процессы. С другой стороны, если запасные элементы использовать в схеме под полной нагрузкой, то в процессе функционирования они будут подвержены воздействию факторов ровно в той же степени, что и основной элемент, и с большой вероятностью запасные элементы могут выйти из строя раньше основного. Поэтому в практике эксплуатации может иметь место использование запасных элементов в теплом режиме, когда они не подвержены в полной мере рабочим нагрузкам, но и с другой стороны, в случае их использования вместо основного элемента, вышедшего из строя, запасные элементы не подвергаются воздействию переходных процессов и более мягко включаются в работу. Поэтому можно сказать, что наличие запасных изделий для отдельных объектов аналогично их резервированию, причем схема резервирования определяется характером использования запасных элементов.
Обратим внимание еще на один вопрос. Заметим, что большинство представленных в литературе подходов к оптимизации состава запасных элементов построены в предположении, что отказавший элемент заменяется идентичным новым объектом. Однако практика эксплуатации объектов на современных производствах такова, что элементы из состава ЗИП подвержены старению в процессе их хранения. Следует также отметить, что отказавшие объекты подлежат восстановлению, и после ремонта пополняют состав запасных элементов. При этом следует иметь в виду, что при выполнении ремонта происходит, как правило, частичное восстановление работоспособности. Часть ресурса объект вырабатывает в процессе предыдущей эксплуатации, и во время ремонта полного восстановления не происходит. Таким образом, будем решать задачу определения состава ЗИП с учетом неполного (частичного) восстановления резервных элементов и выработки ими определенной части ресурса.
Перейдем теперь непосредственно к постановке задачи. Логично заметить, что чем выше кратность резервирования объекта, тем надежней система, в состав которой входит данный объект. С другой стороны, чем больше имеется запасных объектов, тем выше расходы на их приобретение, доставку, хранение и т.п. В результате возникает оптимизационная задача, состоящая в обеспечении высокого уровня надежности систем и оборудования и отвечающая заданным требованиям на материальные затраты, связанные с приобретением, транспортировкой, хранением и прочими расходами, связанными с использованием запасных изделий.
Математическая постановка задачи. Пусть имеется система, состоящая из взаимосвязанных и взаимодействующих элементов, работающих одновременно. В системе функционируют элементы m типов (i = 1, 2, ... m). Будем считать, что каждый элемент работает до отказа. В случае отказа основного элемента он заменяется на резервный из состава запасных. При этом запасной элемент может работать в теплом режиме, и к моменту использования в качестве основного он может выработать часть своего ресурса. В качестве планируемого календарного времени работы системы будем рассматривать интервал времени (0,t0). Обозначим требуемое количество запасных элементов i-го типа через ni, тогда совокупность запасных элементов всех типов можно представить в виде массива (n1, n2, ..., nm). Требуется определить оптимальный состав запасных элементов каждого вида, чтобы максимизировать коэффициент готовности системы на интервале времени работы от 0 до t0. В качестве ограничений в данной задаче будем рассматривать ограничения на затраты, связанные с покупкой комплекта запасных изделий, транспортировкой, хранением и прочими расходами.
Построение модели оптимизации комплекта запасных изделий
Каждый элемент i-го типа имеет свои характеристики надежности. Обозначим через ![]() функцию распределения наработки до отказа элемента i-го типа, через
функцию распределения наработки до отказа элемента i-го типа, через ![]() соответствующую ей плотность распределения. Обозначим расходы на приобретение, доставку и хранение одного элемента i-го типа через Ci , тогда стоимость запасных элементов всех типов для системы в целом будет равна
соответствующую ей плотность распределения. Обозначим расходы на приобретение, доставку и хранение одного элемента i-го типа через Ci , тогда стоимость запасных элементов всех типов для системы в целом будет равна
![]() .
.
Предположим, что все элементы в системе работают независимо, и отказ каждого элемента моментально становится известным оперативному персоналу. В качестве критериальной функции рассмотрим коэффициент готовности анализируемой системы. Он будет выражаться через коэффициенты готовности каждого элемента, входящего в состав системы, и иметь вид [4]
![]() (1)
(1)
где h - кворум-функция или логическая функция работоспособности системы; Ks и Ki - соответственно коэффициенты готовности системы и i-го элемента. Отметим, что если восстановление элемента происходит практически мгновенно, то в формуле (1) вместо коэффициента готовности будет использоваться вероятность безотказной работы.
Задача оптимального выбора комплекта запасных элементов системы для интервала времени ее календарной работы (0,t0) сводится к максимизации нелинейной функции, определяемой выражением (1), при наличии линейного ограничения по стоимости
![]() , (2)
, (2)
где С0 - заданная (допустимая) величина общей стоимости запасных элементов.
Данная задача относится к классу оптимизационных задач нелинейного программирования, так как оптимизируется нелинейный функционал при наличии линейного ограничения.
В приведенной постановке задачи определение характеристик, входящих в ограничения (2), не представляет труда. Остановимся на вопросах определения характеристик надежности элементов и системы в целом с учетом имеющихся запасных объектов. Задачи подобного рода решаются в теории восстановления. Рассмотрим событие, состоящее в том, что на интервале времени произойдет не больше чем ni отказов элементов i-го типа. Обозначим через Tj наработку j-го элемента i-го типа при условии, что произошло (j-1)-е восстановление. Будем считать, что в момент времени t = 0 все элементы системы, в том числе и запасные, новые. Условимся также, что восстановление, т.е. замена отказавшего элемента запасным, происходит за пренебрежимо малое время, практически мгновенно. Определим момент времени, в который произошел ni-й отказ (или ni-е восстановление):
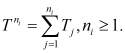 (3)
(3)
В дальнейших выкладках опустим индекс при параметре n. Величины ![]() , называются моментами восстановления.
, называются моментами восстановления.
Задача, решенная в предположении, что все запасные элементы в момент их установки на место отказавшего основного элемента новые, рассмотрена в работе [3].
Рассмотрим теперь метод решения задачи в случае, когда запасные элементы к моменту их установки в систему выработали часть ресурса.
Вначале будем рассматривать структуру с резервированием, в которой имеется один работающий элемент и один элемент резервный. Если основной элемент выходит из строя, то резервный элемент (если он не отказал к этому времени) включается в систему и работает вместо вышедшего из строя основного элемента. Будем рассматривать случай, когда запасной элемент к моменту установки в систему выработал часть своего ресурса. Этот случай с математической точки зрения идентичен случаю, когда запасной элемент работает в режиме теплого резервирования. Рассматриваемая модель имеет достаточно высокую степень общности, так как она объединяет случаи с холодным резервом (когда отказавший элемент заменяется новым) и горячего резервирования (резервный элемент находится под полной нагрузкой, такой же, как и у основного элемента). Отметим, что в случае горячего резервирования после переключения на резервный элемент надежность системы не меняется. Горячее резервирование имеет следующий недостаток: резервный элемент выходит из строя раньше основного с вероятностью 0,5.
Предположим, что наработка до отказа T1 основного элемента имеет функцию распределения F1(t) и плотность f1(t), наработка до отказа резервного элемента T2 имеет функцию распределения F2(t) и плотность f2(t).
Наработка до отказа системы выражается статистикой
![]()
Обозначим ![]() условную плотность распределения наработки до отказа резервного элемента, при условии, что основной элемент отказал в момент
условную плотность распределения наработки до отказа резервного элемента, при условии, что основной элемент отказал в момент ![]() . Ясно, что
. Ясно, что
![]() если
если ![]() .
.
Функция распределения ![]() наработки до отказа структуры дается формулой
наработки до отказа структуры дается формулой
![]() (4)
(4)
В случае холодного резервирования
![]()
и
![]()
В случае горячего резервирования
![]() откуда следует
откуда следует ![]()
В случае теплого резервирования предполагается, что имеет место следующая гипотеза:
![]() для всех
для всех ![]()
где ![]() есть момент времени, который в горячем режиме соответствует моменту y в теплом режиме в том смысле, что
есть момент времени, который в горячем режиме соответствует моменту y в теплом режиме в том смысле, что
![]()
откуда
![]()
Из формулы (4) следует, что при гипотезе H0 [8]
![]()
В частности, если предположить, что распределения времени работы структуры в теплом и горячем режимах отличаются лишь параметрами масштаба, то будем иметь
![]()
для некоторого r>0. То есть, имеем ![]() . В таком случае получаем
. В таком случае получаем
![]() для всех
для всех ![]() .
.
Обобщим данную модель на случай одного основного и (n-1) запасных элементов. Пусть, как и раньше, наработка до отказа основного элемента T1 имеет функцию распределения F1(t) и плотность f1(t), наработка до отказа резервного элемента Tj имеет функцию распределения F2(t) и плотность f2(t), где j=2,n. Наработку до отказа всей структуры (отказ основного и всех запасных элементов) можно записать следующим образом:
![]() .
.
Обозначим функцию распределения наработки до j-того отказа (отказ основного и j-1 запасных элементов) через Sj. Заметим, что S1 = F1. Определим функцию распределения наработки до j-го отказа:
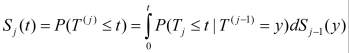 .
.
Точно так же, как в случае двух элементов
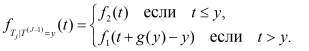
Как и раньше, ![]()
Окончательно получаем:
![]()
Используя данную формулу, можно с помощью итерационных вычислений определить функцию распределения наработки до отказа структуры ![]() (отказ основного элемента и всех запасных). Соответственно, вероятность безотказной работы структуры будет вычисляться по формуле
(отказ основного элемента и всех запасных). Соответственно, вероятность безотказной работы структуры будет вычисляться по формуле
Ki ![]() .
.
Определяя данные величины для всех элементов системы, подставляя их в выражение (1), находим коэффициент готовности системы в целом. Далее переходим к решению оптимизационной задачи функционала (1) при ограничении (2).
Вычисленные таким образом характеристики подставляются в выражение (1), которое будет представлять собой оптимизируемый функционал задачи оптимизации комплекта запасных изделий, в предположении, что к моменту установки в систему запасные элементы вырабатывают часть своего ресурса.
Заключение
Таким образом, можно констатировать, что в предлагаемой работе представлена модель задачи оптимизации комплекта запасных изделий и приборов с учетом старения элементов. В ней сделано предположение о том, что в процессе функционирования системы запасные элементы расходуют часть своего ресурса. Учет старения элементов при оптимизации комплекта запасных изделий приводит к перераспределению требований к формированию ЗИП. Объекты, имеющие на начальном этапе более высокие показатели надежности, могут со временем быстрее расходовать свой ресурс, чем элементы, показатели надежности которых на начальном этапе были ниже. И если на начальном этапе требовалось больше запасных элементов для менее надежных объектов, то по мере выработки ресурса требования к формированию ЗИП могут измениться в сторону других элементов, более быстро расходующих свой ресурс.
Рассмотренная задача определения состава ЗИП относится к категории задач нелинейного программирования. Решение задач такого типа возможно только численными методами.
Рецензенты:
Острейковский Владислав Алексеевич, д.т.н., профессор кафедры информатики и вычислительной техники Сургутского государственного университета ХМАО - Югры, г. Сургут.
Перегуда Аркадий Иванович, д.т.н., профессор Калужского филиала Московского финансово-юридического университета (МФЮА), г. Малоярославец.
Библиографическая ссылка
Антонов А.В., Пляскин А.В., Татаев Х.Н. К ВОПРОСУ ОПТИМИЗАЦИИ КОМПЛЕКТА ЗАПАСНЫХ ИЗДЕЛИЙ С УЧЕТОМ ЧАСТИЧНОЙ ВЫРАБОТКИ ИХ РЕСУРСА // Современные проблемы науки и образования. 2012. № 1. ;URL: https://science-education.ru/ru/article/view?id=5547 (дата обращения: 13.03.2026).



