На итоговой аттестации в 9-х классах по модернизированным программам, предлагаются задачи, в которых требуется решить системы алгебраических, нелинейных уравнений. Школьники испытывают большие затруднения, встречаясь с такими заданиями, особенно, если речь идет о нелинейных системах уравнений. Этот раздел алгебры по праву считается одним из трудных, так как нет единых способов решения систем алгебраических уравнений.
Необходимо помочь школьникам преодолеть трудности при решении алгебраических систем нелинейных уравнений, научить отыскивать наиболее рациональный способ решения систем уравнений, тем самым подготовить выпускника основной школы к сдаче экзамена по математике, продолжению образования в выпускных классах средней школы с профильным обучением, а затем в вузе, где дисциплины математического цикла являются профильными.
Материал статьи излагается как углубленное изучение вопросов, связанных с решением нелинейных систем уравнений в 9 классе, предусмотренных программой основного курса математики.
Предлагаются некоторые способы решения нелинейных систем уравнений. Причем, среди предлагаемых примеров имеются, как достаточно простые, так и сложные.
При решении систем уравнений применяются различные методы:
а) разложение на множители;
б) исключение переменных;
в) алгебраическое сложение;
г) замена переменных;
д) системы однородных уравнений;
ж) метод введения новых переменных;
з) графический метод.
Рассмотрим некоторые методы решения нелинейных систем уравнений.
1. Метод разложения на множители
Метод разложения на множители алгебраических систем двух уравнений с двумя неизвестными заключается в следующем. Если в алгебраической системе
![]()
то всякое решение системы уравнений
![]()
является решением совокупности систем
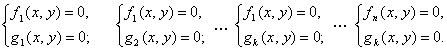
Пример 1. Решить систему
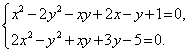
Решение. Так как ![]() , а
, а ![]() или
или
![]() , то получаем:
, то получаем:
![]()
Заметим, что множитель ![]() так как в этом случае правая часть второго уравнения системы также обратилась бы в нуль. Следовательно, система (*) равносильна системе
так как в этом случае правая часть второго уравнения системы также обратилась бы в нуль. Следовательно, система (*) равносильна системе
![]()
![]()
Решим второе уравнение:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Выразив x из первого уравнения и подставив во второе, получили уравнения для нахождения y. В первое уравнение системы вместо y подставляем найденное значение и находим значения x
![]() ,
, ![]() Ответ:
Ответ: 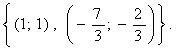
2. Метод исключения одной из неизвестных
Метод исключения неизвестных позволяет последовательно сводить решение данной системы к решению системы (или совокупности систем), содержащей на одну переменную меньше. Этот метод последовательного исключения основан на очевидном утверждении, что система уравнений
![]()
равносильна системе уравнений
![]()
и аналогично для большего числа переменных.
Пример 2. Решить систему 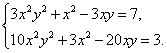
Решение. Левые части уравнений системы содержат одни и те же комбинации неизвестных. Умножим уравнения на подходящие множители с тем, чтобы исключить из системы одно из неизвестных. Из системы исключим ![]() сложив второе уравнение с первым, умноженным на -3. В результате получаем уравнение
сложив второе уравнение с первым, умноженным на -3. В результате получаем уравнение ![]() .
.
Решим данное уравнение путем замены.
Пусть xy = t, тогда ![]() , t1=2, t2=9.
, t1=2, t2=9.
Таким образом, исходная система распадается на системы:
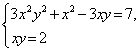 и
и 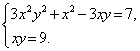
В первом случае находим x2=1. Если x=1 то y=2 , а если x=-1, то y=-2.
Во втором случае, исключая , получаем x2=-209. Поэтому вторая из двух последних систем не имеем действительных решений.
Ответ: {(1;2),(-1;-2)}.
3. Метод алгебраических преобразований уравнений системы
Уравнения системы можно складывать, вычитать, умножать на число, перемножать, делить, соблюдая при этом возможность выполнения таких операций. Заметим, что следствие системы, получаемое в результате алгебраических преобразований, содержит все решения исходной системы, и, кроме того, оно может содержать лишние корни.
Поэтому: 1) если следствие не имеет решений, то и исходная система не имеет решений; 2) если решениями следствия окажутся действительными числа, то их нужно подставить в исходную систему и проверить, являются ли они ее корнями; 3) если решениями следствиями окажутся алгебраические выражения, то их нужно рассматривать совместно с уравнениями исходной системы. В этом случае получим равносильную систему или совокупность систем.
Пример 3. Решить систему 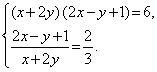
Решение. ОДЗ: ![]()
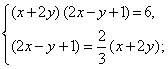
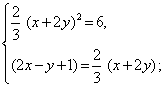
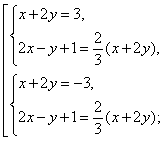
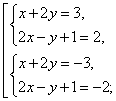
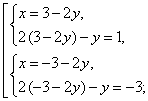
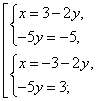
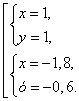
Ответ: {(1; 1), (-1,8; -0,6)}
4. Метод замены переменных
Метод замены неизвестных основан на следующем утверждении.
Пусть дана система уравнений ![]() и пусть система
и пусть система ![]() имеет k различных решений
имеет k различных решений ![]() .
.
Тогда система (1) равносильна совокупности k систем
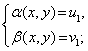
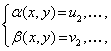
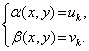
Пример 4. Решить систему 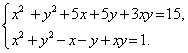
Решение. 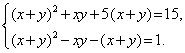
Произведем замену. Пусть ![]() Тогда
Тогда 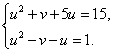
Складывая уравнения, получим ![]()
![]()
![]()
Преобразуем первое уравнение:
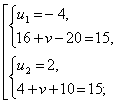
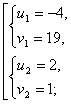
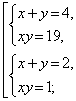
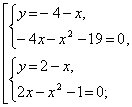
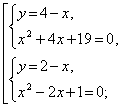
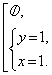
Ответ: {(1; 1)}
5. Системы однородных уравнений
Система двух уравнений с двумя переменными вида
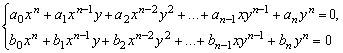
называется однородной (левые части обоих уравнений однородные многочлены степени n от двух переменных).
Однородные системы решаются комбинацией двух методов: линейного преобразования и введения новых переменных.
Пример 5. Решить систему 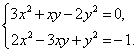
Решение. Первое уравнение системы однородное (напомним, что уравнение вида f(x,y)=0 где f(x,y) - однородный многочлен - называется однородным уравнением). Заметим, что если положить y=0 то из однородного уравнения 3x2+xy-2y2=0 находим x=0. Но пара чисел (0;0) не удовлетворяет второму уравнению системы, поэтому y≠0 и, следовательно, обе части однородного уравнения 3x2+xy-2y2=0 можно разделить на y2 (это не приведёт к потере корней).
Получим ![]() и
и 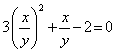 , откуда находим, что
, откуда находим, что ![]() или
или ![]() , т.е. x= - y или
, т.е. x= - y или ![]() .
.
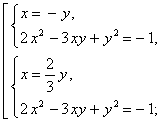
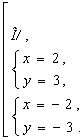 Ответ:
Ответ: ![]()
Типичные ошибки при решении систем и методы их устранения
При решении некоторых систем иногда происходит потеря корней в ответе или появляются посторонние корни. Основная причина этого заключается в том, что осуществляются правдоподобные рассуждения, но теряется контроль над равносильностью переходов от одной системы к другой. Для того чтобы избежать подобных ошибок, нужно знать природу их появления и на определенном этапе решения произвести необходимые преобразования, проверку решения и т.д.
В качестве таких примеров рассмотрим решение нескольких систем нелинейных уравнений.
Пример 1. Решите систему уравнений 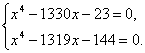
Неправильное решение. Вычтем из первого уравнения системы второе уравнение. Получим![]() откуда x =11.
откуда x =11.
В этом случае корень уравнения, полученный после эквивалентного преобразования (вычли второе уравнение из первого), не проверили. Чтобы избежать подобной ошибки, необходимо после вычитания одного уравнения из другого решать систему уравнений, в которой обязательным является наличие уравнения, полученное после вычитания и одного из первоначальных уравнений.
Неправильный ответ: {11}.
Правильное решение. Выполним эквивалентные преобразования:
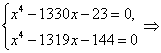
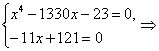
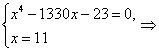
![]()
![]()
Таким образом, при решении системы уравнений, необходимо записать такое же количество уравнений, которое было в условии, чтобы не получить посторонний корень.
Правильный ответ: ![]() .
.
Пример 2. Решить систему уравнений
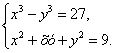 (1)
(1)
Решение. Выполним тождественное преобразование: разделим первое уравнение системы на второе уравнение, получим:
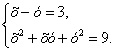 (2)
(2)
Решая систему методом подстановки, получим множество решений: {(3;0); (0;3)}.
Система (2) получена из системы (1) делением на число, отличное от нуля, поэтому системы (1) и (2) эквивалентны.
При решении систем нелинейных уравнений необходимо помнить о том, что такое тождественное преобразование как деление одного уравнения на другое не всегда приведет к правильному решению, так как может произойти потеря корня. Покажем это на следующем примере.
Пример 3. Решить систему уравнений
![]() (3)
(3)
Решение. Выполним тождественное преобразование: разделим первое уравнение системы на второе уравнение, получим:
![]() Ответ:
Ответ: ![]()
Но в этом случае произошла потеря решения {(2;0)}. Это произошло потому, что при делении не было наложено условие ![]() . Рассматривая условие
. Рассматривая условие ![]() , получаем х = 2.
, получаем х = 2.
Значит, метод деления одного уравнения на другое не безупречен, т.е. при переходе от системы 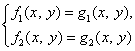 к системе
к системе 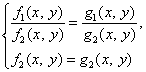 можем потерять решения.
можем потерять решения.
СПИСОК ЛИТЕРАТУРЫ:
- Азаров А.И., Барвенов С.А., Федосенко В.С., Шибут А.С. Системы алгебраических уравнений. Текстовые задачи. Справочное пособие для абитуриентов и школьников. 1998. - 288 с.
- Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 11 класса. Учеб. пособие для учащихся шк. и классов с углубл. изуч. математики. 4-е изд. - М.: Просвещение, 1995. - 335 с.
- Галицкий М.Л., Гольдман А.М., Звавич Л.И. Сборник задач по алгебре для 8-9 классов. Учеб. пособие для учащихся шк. и классов с углубл. изуч. курса математики. М.: Просвещение, 1992. - 271 с.
- Самусенко А.В., Казаченок В.В. Математика: Типичные ошибки абитуриентов. 2-е изд., испр. - Мн.: Выш. шк., 1995.- 185 с.
- Шарыгин И.Ф., Голубев В.И. Факультативный курс по математике: Решение задач. Учеб. пособие для 11 класса средней школы. - М.: Просвещение, 1991. - 384 с.
Библиографическая ссылка
Седакова В.И., Рочева И.Г. РЕШЕНИЕ НЕЛИНЕЙНЫХ СИСТЕМ УРАВНЕНИЙ В КЛАССАХ С УГЛУБЛЕННЫМ ИЗУЧЕНИЕМ МАТЕМАТИКИ // Современные проблемы науки и образования. 2007. № 5. ;URL: https://science-education.ru/ru/article/view?id=548 (дата обращения: 19.02.2026).



