Введение
Актуальным направлением в области разработки образовательных технологий являются методы интерактивного обучения. Такие методы, которые также называют дистанционными, успешно внедряются в практику. Теоретическим представлением таких курсов могут служить их математические модели. Очевидно также, что наиболее перспективны такие интерактивные учебные курсы, которые приближены (адаптированы) к обучаемому [2,5].
В данной статье рассматривается моделирование прохождения учебного курса с использованием двух методологий - сетей Петри и цепей Маркова. Предполагается, что курс преподается студентам различных форм обучения, поэтому модель курса адаптирована к трем категориям обучаемых.
Постановка задачи
Рассмотрим некий учебный курс, состоящий из m модулей, причем каждый модуль соответствует какой-либо теме курса.
В данном курсе предусмотрена адаптация к объему изучаемого материала и его сложности. Наиболее естественно ввести три категории обучаемых: 1-й уровень - студенты очной пятигодичной формы обучения; 2-й уровень - студенты очной ускоренной формы обучения; 3-й уровень - студенты заочной формы обучения.
Следует заметить, что присвоение определенного уровня различным категориям студентов не является чем-то неизменным. Процедура адаптации как раз и позволяет студенту любой категории выбрать для себя свою последовательность прохождения разделов, т.е. свою траекторию изучения курса. Под траекторией обучения будем понимать прохождение учащимся разделов курса с возможностью смены уровня сложности в зависимости от оценки, полученной при тестировании на предыдущем этапе.
Каждый модуль содержит теоретический и справочный материал, задания для самостоятельной работы, а также набор контрольных материалов для самопроверки и получения оценки.
Процесс прохождения учащимся учебного модуля заключается в следующем [4]. Из базы учебных модулей извлекается очередная порция теоретического материала, которую предлагается освоить обучаемому. После того, как обучаемый окончил изучение этого материала, система приступает к тестированию. Из базы тестов выбирается тестовый материал и предъявляется обучаемому, который готовит и вводит в систему ответы на тестовые задания. Эти ответы анализируются системой оценивания, которая принимает решение:
- ответы верные, в этом случае изучение данного модуля завершается, и возможен переход к следующему модулю, а также повышение уровня сложности;
- ответы неточные, в этом случае обучаемый должен изучить дополнительный материал и затем пройти повторное тестирование;
- ответы абсурдные, в этом случае обучаемый должен изучить материал модуля с самого начала; также возможно понижение уровня сложности.
Одним из удобных инструментов моделирования процесса интерактивного обучения является методология раскрашенных (цветных) сетей Петри - Coloured Petri Net (CPN) [1]. Особенность этой методологии состоит в том, что она моделирует системы в терминах «условия - события», что позволяет исследовать динамику работы системы. Применение сетей Петри позволяет наглядно представить динамику прохождения учебного курса, а также служит основой для исследования свойств моделируемой системы и создания имитационных алгоритмов. Определенным неудобством этой модели является то, что динамические параметры процесса можно оценивать только с помощью имитационного моделирования.
Другой подход к моделированию процесса интерактивного обучения основан на том, что, как отмечено рядом авторов еще в 50-е годы, этот процесс при определенных допущениях может быть представлен как цепь Маркова [6].
Модель представляет собой ориентированный граф, содержащий узлы и дуги. При этом каждый узел моделирует один из шагов процесса изучения курса. Дуги между узлами моделируют последовательность выполнения шагов, они помечаются вероятностями перехода от одного узла к другому.
В дальнейшем мы остановимся на курсе, разбитом на восемь модулей (наиболее реальное разбиение для годового учебного курса). Фиксирование числа модулей позволит работать с моделями в реальном представлении.
Обозначим модули таким образом:
- модули М1-М4 и М8 содержат учебный материал. В каждом из этих модулей представлены три варианта учебного материала, соответствующего различным уровням сложности;
- модуль М5 - индивидуальные задания, имеют три уровня сложности;
- модуль М6 - задания для коллоквиума, имеют один, общий для всех, уровень сложности.
- модуль М7 - курсовая или расчетно-графическая работа предусмотрена только для студентов очной формы обучения и содержит, соответственно, два уровня сложности.
Динамическая модель курса в виде иерархической раскрашенной сети Петри
Ввиду сложности и многовариантности прохождения курса, его модель целесообразно строить в виде двухуровневой иерархической сети [3].
На рисунке 1 приведена модель этого курса в виде раскрашенной сети Петри верхнего уровня. Каждый из описанных выше модулей представлен в виде непримитивного перехода t1, t2, ....t8 и соответствующей позиции P1, ..........P8. Каждому переходу t1,....t8 соответствует сеть Петри нижнего уровня, описывающая выполнение соответствующего модуля.
Рассмотрим использованные цветовые множества (ресурсы системы).
Color INT = integer - вспомогательные переменные.
Color SPEC = (sw5, sw3, swz, ist, ac5, ac3, acz) - обозначения образовательных программ.
Color LEVEL = (l1, l2, l3) - уровень сложности.
Color STUD = integer with 1,...,N - код студента в системе, N - общее число обучаемых студентов.
Color LEARN = product STUD*SPEC*LEVEL timed - код обучаемого.
Color MOD = integer with 1,...,8 - номера учебных модулей.
Color TIMEMOD = product (integer with tminM,...,tmaxM)*MOD*LEARN declare random - время изучения модуля обучаемым - случайная величина, находящаяся в пределах от tminM до tmaxM.
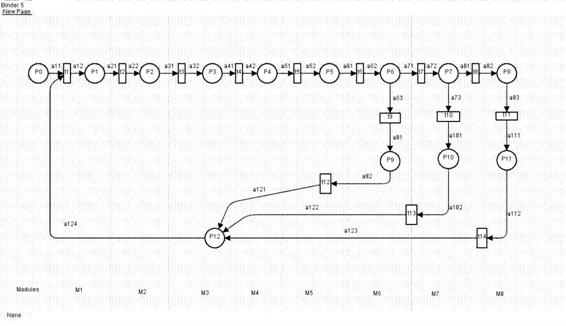
Рис. 1. Раскрашенная сеть Петри, моделирующая прохождение курса
При функционировании системы используется ряд констант, которые характеризуют среднее нормативное время выполнения студентом каждого модуля при каждом уровне сложности - величины τkj, где k=1,...5,8 - номера модулей; j=1,2,3 - номера уровней сложности. При k=6 уровень сложности один: j=1, а при k=7 - два: j=1,2.
Рассмотрим теперь выражения на дугах, определяющие алгоритм функционирования системы. Все модули М1-М8 имеют входные дуги ak1 (k=1,...,5,7,8), выражения на которых имеют вид 1'(st, sp, lv). Выражения на выходных дугах ak2 (k=1,...,5,7,8) имеют такой же вид 1'(st, sp, lv), однако значение переменной lv (уровень сложности) зависит от значения tmod, т.е. от фактического времени, затраченного на прохождение модуля. Переход на новый уровень сложности осуществляется случайным образом, при этом вероятности зависят от значения величины tmod предыдущего модуля. Выражения на дугах модуля М6 имеют вид, аналогичный рассмотренному ранее: на а61 - 1'(st, sp, lv), на а62 - 1'(st, sp, lv), причем изменения уровня сложности не происходит. Выражения на дугах а63, а73 определяются логическими функциями:
if Ei then 1'(st, dp, lv), i=6,7, где Е6 = if(sp=swz or sp=ac3 or sp=acz); E7 = if(sp=sw3 or sp=ac3 or sp=acz).
Выражения на дугах a71 и a81 имеют вид: a71:
if not E6 then 1'(st, sp, lv); a81: if not E7 then 1'(st, sp, lv).
Логические функции в приведенных выражениях определяют момент окончания процесса обучения в зависимости от формы обучения.
Выражения на остальных дугах: на a91, a101, a111 - 1'(st, sp, lv); на a92, a102, a112 - 1'(st+1) - переход к следующему студенту; на a121, a122, a123, a124 - 1'st.
Начальная маркировка сети:
![]()
- сведения обо всех обучаемых с указанием кода студента, специальности и начального уровня сложности; m12=1'1 - установка кода первого по списку студента. Остальные позиции сети в начальный момент времени не имеют ресурсов.
После завершения работы сети в позициях Р9, Р10, Р11 оказываются сведения обо всех студентах соответствующих специальностей, общее время прохождения каждым из них всего курса и уровень сложности по последнему пройденному блоку; m12=1'N - номер последнего прошедшего обучение студента.
Модели отдельных модулей
Рассмотренные в этом разделе модели отдельных модулей курса, образующих нижний уровень иерархии, приводятся с использованием двух формализмов - сетей Петри и соответствующих цепей Маркова, поскольку процессы в обучающей системе имеют случайных характер. При этом номера позиций Pi в сетях Петри и номера состояний Si в цепях Маркова взаимно однозначно соответствуют друг другу. Во всех марковских цепях добавлены поглощающие состояния для того, чтобы время работы модуля было конечным.
1. Модули М1-М4 и М8 содержат следующие состояния (рисунок 2):
P1, S1 - получение задания;
P2, S2 - работа с компьютерной обучающей или тестирующей программой;
P3, S3 - защита выполненной работы;
P4, S4 - изучение дополнительного материала;
P5, S5 - получение зачета по модулю.
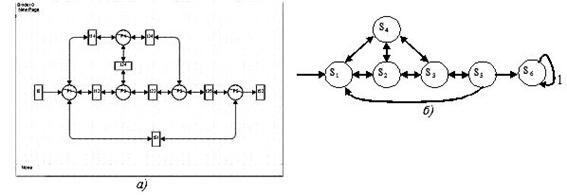
Рис. 2. Структура модулей с М1 по М4, а также М8: а) сеть Петри; б) цепь Маркова
Матрица переходных вероятностей для рассматриваемой группы модулей имеет вид:
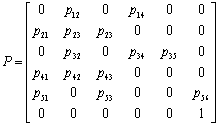
2. Модули М5 и М6 включают следующие состояния (рисунок 3):
P1, S1 - получение задания;
P2, S2 - выполнение задания;
P3, S3 - изучение дополнительного материала;
P4, S4 - получение зачета по модулю.
Матрица переходных вероятностей для модуля М5 и М6 имеет вид:

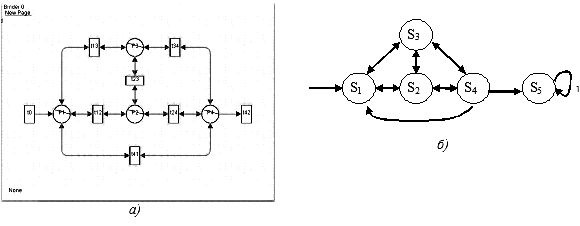
Рис. 3. Структура модулей М5 и М6: а) сеть Петри; б) цепь Маркова
5. Модуль М7 включает следующие состояния (рисунок 4):
P1, S1 - получение задания на курсовую работу;
P2, S2, P3, S3, P4, S4 - выбор уровня сложности работы;
P5, S5 - защита выполненной работы;
P6, S6 - получение оценки за работу и зачета по модулю.
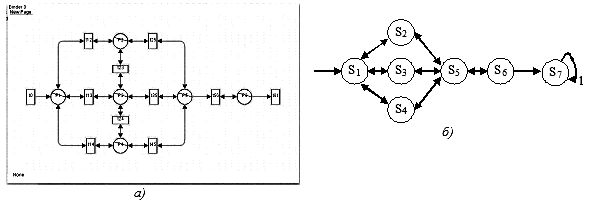
Рис. 4. Структура модуля М7: а) сеть Петри; б) цепь Маркова
Матрица переходных вероятностей для модуля М7 имеет вид:
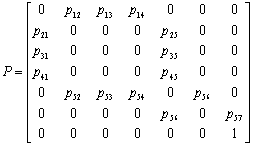
Моделирование процесса адаптации
В данном разделе более подробно рассмотрена модель процесса адаптации, т.е. перехода обучаемого с одного уровня сложности изучения материала на другой.
Под адаптацией в теории управления понимают «процесс изменения параметров и структуры системы, а возможно, и управляющих воздействий на основе текущей информации с целью достижения определенного, обычно оптимального, состояния системы при начальной неопределенности и изменяющихся условиях работы» [7].
Применяя это определение к процессу обучения, можно сказать, что адаптация в обучающей системе - процесс изменения параметров и структуры модели объекта (обучаемого) и обучающих воздействий на основе текущей информации, получаемой в ходе обучения, с целью достижения оптимального состояния объекта при его начальной неопределенности и изменяющейся среде. Начальная неопределенность связана с почти полным отсутствием в обучающей системе информации об обучаемом.
При этом, если взять за основу сеть Петри верхнего уровня (рис. 1) и сосредоточиться только на моделировании процесса перехода между уровнями сложности, то мы получим обыкновенную сеть Петри, изображенную на рис. 5 и соответствующую ей цепь Маркова (рис. 6).
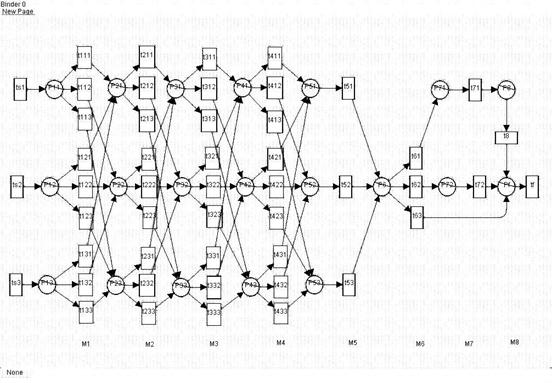
Рис. 5. Сеть Петри, моделирующая процесс изучения курса
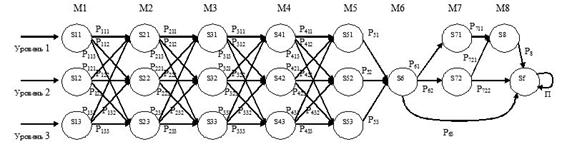
Рис. 6. Цепь Маркова, моделирующая вероятностный процесс прохождения курса
Как и ранее, на приведенных рисунках позиции pij в сети Петри взаимно однозначно соответствуют состояниям Sij в цепи Маркова.
Матрица вероятностей переходов в цепи Маркова в соответствии с рисунком 6 имеет вид:
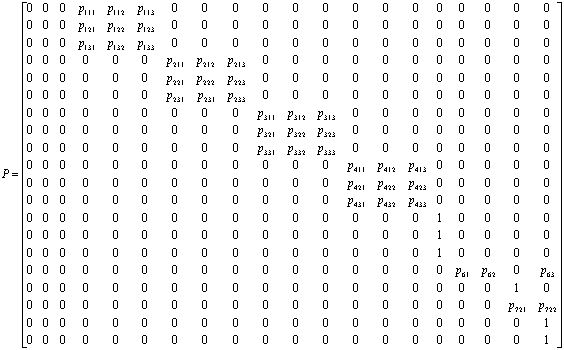
Поясним обозначение вероятностей на рисунке 6 и в соответствующей матрице вероятностей. Величина pkjl означает вероятность перехода с j-го уровня k-го модуля на l-й уровень k+1-го модуля для k=1,...,4,7. При k=5 и 6 вероятности имеют два индекса, т.к. в модуле М6 не выделяются уровни сложности.
СПИСОК ЛИТЕРАТУРЫ:
- Jensen, K. Colored Petri Nets: Basic Concepts, Analysis Methods and Practical Use. [Текст]. - Berlin: Springler. - Vol.1 - 1996, Vol.2 - 1997, Vol.3 - 1997.
- Башмаков, А.И. Разработка компьютерных учебников и обучающих систем. [Текст] / А.И. Башмаков, И.А. Башмаков - М.: Информационно-издательский дом "Филинъ". - 2003. - 616 с.
- Доррер, А.Г. Динамическое моделирование процесса интерактивного обучения. [Текст] / А.Г. Доррер // Материалы Всероссийской научно-практической конференции «Лесной и химический комплексы: проблемы и решения». - Красноярск: СибГТУ. - 2005. - C.253-258.
- Доррер, А.Г. Моделирование и разработка интерактивных обучающих систем с адаптацией. [Текст] / А.Г. Доррер // Материалы IX Всероссийской научно-практической конференции «Проблемы информатизации региона. ПИР-2005». - Красноярск: ИПЦ КГТУ. - 2005. - с.147-152.
- Доррер, А.Г. Модель процесса интерактивного обучения как автомат с линейной тактикой. [Текст] / А.Г. Доррер // Материалы III Всероссийской научно-практической конференции студентов «Молодежь и современные информационные технологии». - Томск: ТПУ. - 2005.
- Доррер, Г.А. Моделирование вычислительных систем: Учебное пособие [Текст]. - Красноярск: КГТУ. - 2004. - 188с.
- Растригин, Л.А. Адаптивное обучение с моделью обучаемого. [Текст] / Л.А. Растригин, М.Х. Эренштейн - Рига: Зинатне. - 1988. - 160с.
Библиографическая ссылка
Доррер А.Г., Иванилова Т.Н. МОДЕЛИРОВАНИЕ ИНТЕРАКТИВНОГО АДАПТИВНОГО ОБУЧАЮЩЕГО КУРСА // Современные проблемы науки и образования. 2007. № 5. ;URL: https://science-education.ru/ru/article/view?id=547 (дата обращения: 25.02.2026).



