Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Королева С.В. 1

---

1 ФГБОУ ВПО «Ивановский институт Государственной противопожарной службы МЧС России», Иваново

Современные методы исследования в медицине повышают требования к качеству и надежности используемой статистической обработки в проводимом эксперименте. Одной из актуальных проблем является необходимость объединения в одной наиболее оптимальной (желательной) для пациента характеристике нескольких показателей, значительно различающихся по размерам и представлению. Изучена возможность использования в качестве многофакторного анализа обобщенной функции желательности Харрингтона. Доказано, что данный метод позволяет объединить в однотипных, одномерных характеристиках разномерные качественные и количественные показатели, что позволяет осуществить многомерный анализ пакета значений или функций. Показано, что односторонние и двусторонние ограничения позволяют охватить все возможные варианты исходных показателей. Приведен клинический пример использования функции желательности для сравнения эффективности различных методов лечения по показателям функции суставов. Продемонстрирована возможность объективного сравнения результатов лечения при одинаковых субъективных характеристиках.

Статья в формате PDF

240 KB

функция желательности Харрингтона

многофакторный анализ

медико-биологический эксперимент

1. Гланц. С. Медико-биологическая статистика / пер. с англ. – М. : Практика, 1998. – 459 с.

2. Гринхальх Т. Основы доказательной медицины / пер. с англ. – М. : ГЭОТАР-Медиа, 2006. – 240 с.

3. Зазнобина Н.И. Оценка экологической обстановки в крупном промышленном центре с помощью обобщенной функции желательности (на примере города Нижнего Новогорода) // Вестник Нижегород. ун-та им. Н.И. Лобачевского. – 2007. – № 2. – С. 115–118.

4. Королева С.В. Клинико-патогенетическое значение кинематической нестабильности коленных суставов в развитии остеоартроза, диагностика и дифференцированная коррекция : автореф. дис. … докт. мед. наук. – Иваново, 2007. – 34 с.

5. Кузьмичев В.Е. Исследование способов изменения показателей свойств деталей при изготовлении одежды : метод. указания / В.Е. Кузьмичев, Г.К. Попова. – Иваново, 1992. – 27 с.

6. Маркова Е.В. Планирование эксперимента в условиях неоднородностей / Е.В. Маркова, А.В. Лисенков. – Л. : Наука, 1973. – 270 с.

Решить данную проблему возможно. Одним из вероятных способов оценки качества пакета характеристик и свойств для анализа полученных результатов является использование обобщенной функции желательности Харрингтона [5], широко применяемой в психифизиологических и экологических исследованиях [3]. В основе построения обобщенной функции лежит идея преобразования полученных значений показателей свойств (в различных единицах измерения, в том числе с качественными, эстетическими, психологическими и личностными характеристиками) в безразмерную шкалу желательности.

Назначение шкалы желательности - установление соответствия между полученными значениями показателей свойств и оценками экспериментатора желательности того или иного показателя для функции органа, системы и в целом организма человека. Стандартные отметки по шкале желательности не являются строго обязательными. На основании имеющегося опыта можно рекомендовать следующие стандартные градации (табл. 1).

Таблица 1 - Стандартные отметки по шкале желательности

Выбор отметок на шкале желательности 0,63 и 0,37 объясняется удобством вычислений: 0,63»1-(1/е), 0,37»1/е. Значение di = 0,37 обычно соответствует границе допустимых значений, т.е. для медицинского эксперимента это может быть критерий принятия решения, например для хирургической коррекции. Для получения единой, обобщенной оценки необходимо задаться наиболее желательными значениями отдельных принятых к анализу показателей (количественных, качественных, эстетических и др.). Эти значения для отдельных показателей можно установить по рекомендациям, стандартам. Если данный анализ положен в основу выводов, то значения для отдельных параметров целесообразнее установить в «пилотном» исследовании эксперимента. Установить границы допустимых значений (для «удовлетворительного» или «отличного» результата). Если такие данные отсутствуют (что вероятно только для абсолютно инновационных исследований), то ограничения для показателей делаются на основании опыта и прогностической интуиции экспериментатора.

В зависимости от «качества» показателя можно устанавливать односторонние или двусторонние ограничения. Если улучшение общей характеристики происходит только при однонаправленном изменении показателя (уменьшении или увеличении) - ограничение носит односторонний характер, а линия графика задается уравнением d = exp [-exp (-y)]. За начало отсчёта 0 по оси абсцисс выбрано значение, соответствующее желательности 0,37. Выбор именно этой точки связан с тем, что она является точкой перегиба кривой, что в свою очередь создаёт определённые удобства при вычислениях. То же самое верно для значения желательности, соответствующего 0,63. Выбор этой кривой не является единственной возможностью. Однако она возникла в результате наблюдений за реальными решениями экспериментаторов и обладает такими полезными свойствами, как непрерывность, монотонность, гладкость. Если изменение параметра вероятно в обе стороны от оптимальных значений, то ограничение носит двусторонний характер.

В предлагаемом далее практическом клиническом примере применения функции желательности оценивается пакет значений кинематической, функциональной стабильности суставов нижних конечностей при остеоартрозе коленных суставов с использованием стабилометрии - аппаратно-компьютерной оценки функции равновесия. Для показателей стабилограмм «FrX» и «60X» установлены односторонние ограничения (изменение значений от «0» в одностороннем направлении), в виде y_i ≥ y_max, где y_i - значение показателя. Для «ОЦМ Х» и «угла наклона колебаний» - двусторонние ограничения (изменения получаемых значений стабилографии происходит от «0» в обе стороны). Следует отметить, что двусторонние ограничения оказались сложны для оценки откликов, т.к. жесткость «привязки» к шкале при необходимости интерпретации в обе стороны от 0 создали дополнительные трудности.

Таблица 2 - Односторонние и двусторонние ограничения для показателей стабилограммы (пример)

На основании полученных результатов можно построить графики желательности (рис. 1).

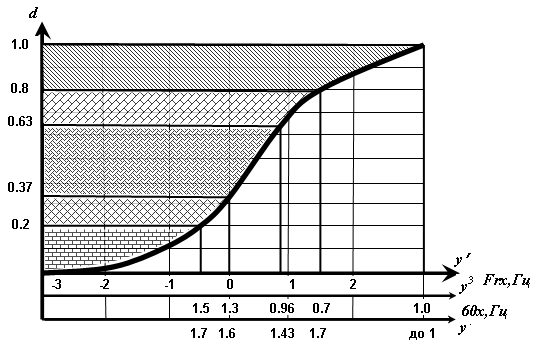
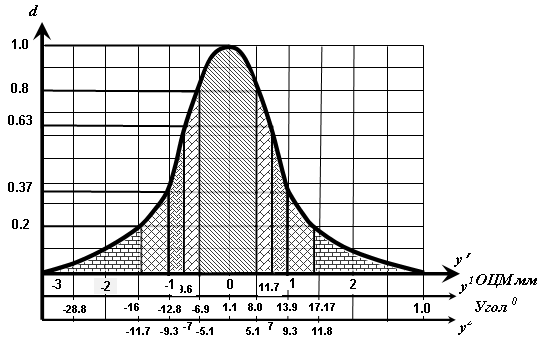
Рис. 1. Графики функции желательности для показателей свойств, ограничиваемых с одной и двух сторон

Построение одностороннего графика необходимо начинать с желательности «плохо», т.к. ей соответствует частный отклик у′ = 0,00 (верхняя ось абсцисс). Необходимо учесть при выборе значений желательности, что очень плохими считаются показатели наихудшей функции (например, показатели, являющиеся «пороговыми» для назначения хирургического лечения при заболеваниях суставов, инвалидизации и т.д.). Остальные клетки заполняются экспериментатором с учетом существующей информации, данными «пилотных» исследований и представлений о том, какие значения отклика соответствуют оценкам «очень хорошо», «хорошо», «удовлетворительно». Та же последовательность при построении двустороннего графика.

Далее для каждого показателя у_i построить оси, параллельные у′, и нанести на них значения желательности из сводных таблиц (аналогичных табл. 2). По значениям, полученным в результате эксперимента, используя графики функции желательности, можно найти для каждого у_ji соответствующее значение d_ji. Значит, можно провести преобразование частных откликов (результатов Вашего личного эксперимента) в частные функции желательности.

Далее приступить к построению обобщенного параметра D - обобщенной функции желательности Харрингтона:

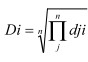, где Di - обобщенный параметр Харрингтона,  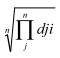- корень степени количества анализируемых свойств частных откликов (в приводимом примере n = 4).

Если хотя бы одна частная желательность d_ji = 0, то и обобщенная функция D_i = 0. Это значит, что данный пакет не может быть применен, т.к. один из показателей не соответствует нормам. Если все d_ji = 1, то и D_i = 1, это пакет наилучший. Т.е. комбинация показателей пакета - оптимальная (лучшее состояние органа, системы, функции организма в целом).

В обобщенную функцию желательности могут входить разнообразные отклики, технологические и социально-экономические показатели, эстетические и экспертные оценки. Обобщенная функция желательности удовлетворяет всем необходимым требованиям, предъявляемым к параметрам оптимизации. Шкала желательности Харрингтона - количественный, однозначный, единый, универсальный показатель качества объекта, как параметра оптимизации. Функция обладает свойствами эффективной и статической чувствительности, хотя и не лишена отдельных недостатков. Так, все параметры принимаются равнозначно «ценными», хотя это не всегда истинно.

В качестве примера приведем решение задачи сравнения эффективности использования нового метода лечения в новой программе реабилитации пациентов с гонартрозом. Из обеих групп наблюдения случайным образом взяты 2 пациента, выбранные значения до и после лечения заведены в разработанные графики. В результате функция желательности D по объективным показателям стабилометрии у больного С., 53 лет, в динамике предлагаемого лечения изменилась с 0,65 до 0,78, а у больной К., 50 лет, со стандартным лечением - с 0,69 до 0,70. При этом оба пациента указали на улучшение самочувствия в виде уменьшения боли. Несмотря на то что оба пациента остались в поле «хорошо» (0,63-0,80), можно сделать вывод о повышении эффективности реабилитации при применении нового метода у больного С., 53 лет (суммарная составляющая по шкале желательности увеличилась в абсолютных значениях). В то же время не происходит значимого улучшения функциональных параметров у больной К., 50 лет, из группы стандартного лечения. Применение функции Харрингтона позволило оценить влияние нового метода: в 68% случаев у пациентов экспериментальной группы состояние кинематической стабильности переводилось в поле «хорошо», в то время как аналогичный показатель в группе пациентов стандартной терапии составил только 33%.

Таким образом, применение функции желательности можно рекомендовать для широкого использования в медико-биологических исследованиях.

Рецензенты:

Авитисов П.В., д.м.н., профессор, зав. кафедрой медико-биологической и экологической защиты ФГБОУ ВПО «Академия гражданской защиты МЧС России», Московская обл. г.о. Химки.

Ясинский Ф.Н., д.ф.-м.н., профессор кафедры высшей математики и информатики ФГБОУ ВПО «Ивановский институт ГПС МЧС России», г. Иваново.

Библиографическая ссылка