Сетевое научное издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 0,936

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Авдеева Д.К. 1 Вылегжанин О.Н. 1 Пеньков П.Г. 1 Небаба С.Г. 1

---

1 ГОУ ВПО «Национальный исследовательский Томский политехнический университет»

Рассмотрены особенности численной реализации фильтра для регистрации биоэлектрических потенциалов, основанного на применении процедуры фазовой модуляции гармоники импульса специальной формы гармониками измеряемого сигнала с шумом. Показано, что для получения максимального значения параметра модуляции необходимо обеспечить попадание значений начальной фазы опорного импульса и импульса с измеряемым сигналом на концы квазилинейного участка зависимости значения этой фазы от соотношения высот ступеней импульса. Приведен алгоритм расчета параметров опорного импульса и коэффициента усиления измеряемого сигнала, обеспечивающий это условие. Предложены методы отбора комбинаторных частот, возникающих при фазовой модуляции с амплитудами выше заданного порога. Проведены модельные расчеты для заданного сигнала со случайным шумом.

Статья в формате PDF

458 KB

расчет комбинационных частот.

фазовая модуляция

фильтрация

измерение биоэлектрических потенциалов

1. Авдеева Д.К. Способ измерения сигналов произвольной формы в присутствии случайных шумов // Патент РФ № 2133474.1999. Бюл. № 20.

2. Авдеева Д.К., Вылегжанин О.Н., Рыбалка С.А. Метод выделения полезного сигнала при помехе, случайной по фазе // Успехи современного естествознания. – 2010. – № 1.– С. 132-135.

3. Андре Анго. Математика для электро- и радиоинженеров. – М.: Наука,1967. – 780 с.

4. Гоноровский И.С. Радиотехнические цепи и сигналы: учебник для ВУЗов. – 4-е изд. – М.: Радио и связь, 1986. – 512 с.

5. Картьяну Г. Частотная модуляция. – Бухарест: Издательство Меридиане,1964. – 673 с.

В настоящей работе обсуждаются особенности численной реализации процедуры формирования такого фильтра.

Как было показано в [2], подобный фильтр может быть построен с использованием опорного импульса специального вида, показанного на рис.1.

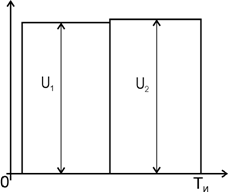
Рис. 1. Форма опорного импульса

Импульс имеет две прямоугольные ступени с амплитудами U₁ и U₂ соответственно, общая длительность ступеней немного меньше длительности интервала наблюдения Т_И.

Как показали результаты анализа, при соотношениях амплитуд ступеней сигнала и отношении длительности интервала измерения к общей длительности ступеней, близких к 1, увеличивается чувствительность фазы к изменению напряжения (амплитуды ступени U₂). При этом зависимость фазы от D (отношение амплитуды второй ступени к амплитуде первой) M (отношение длительности интервала измерения к суммарной длительности ступеней ) имеет вид:

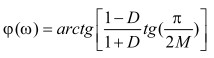
Если поместить на интервале от Т_И/2 до Т_И опорного импульса измеряемый сигнал с помехой, то любая его гармоническая составляющая w_i будет модулировать по амплитуде и фазе гармонику опорного импульса в виде [3,4,5]:

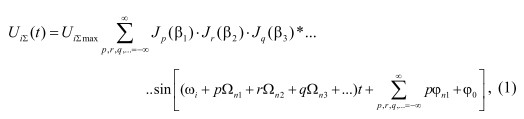
, (1)

Где β- глубины модуляции ( β_i=φ₀ - φ_i, , т.е. разность значений фазы опорного импульса и модулирующей гармоники), Ω­частоты, а φ­ начальные фазы модулирующих гармоник. Из выражения (1) следует, что модулируемое колебание содержит целый набор комбинационных частот, отстоящих от основной частоты выше и ниже на величину .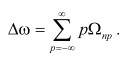

Из приведенных рассуждений вытекает следующая схема применения фильтра. Формируется опорный импульс, на нижнюю ступень которого помещается фрагмент аддитивной суммы измеряемого сигнала и шума. Выполнив преобразование Фурье для этого фрагмента, можно представить его в виде линейной комбинации гармоник разложения Фурье, которые и будут модулировать опорный импульс. Важным параметром, определяющим эффективность описываемого фильтра, является глубина модуляции. Анализ показывает, что максимальная глубина фазовой модуляции может быть равна p (гармоники находятся в противофазе). Но в реальных расчетах рекомендуется обеспечивать попадание фазы опорного импульса и фазы импульса с измеряемым фрагментом сигнала на квазилинейный участок графика зависимости фазы от параметра φ(D) .  Для этого был предложен следующий алгоритм - выбираем значение M, первую ступень опорного импульса принимаем равной 1, а затем вычисляем значение D , которое обеспечивает попадание начальной фазы основной гармоники на нижний конец квазилинейного участка кривой φ(D). Для этого вычисляется максимальное значение второй производной φ(D) по D, которое соответствует значению D=0. Тогда квазилинейный участок кривой  соответствует значениям D≅0.10 от этого значения. Сформировав таким образом опорный импульс, вычислим среднее значение измеряемого фрагмента сигнала  и умножим этот фрагмент на коэффициент , где  - среднее значение фрагмента сигнал плюс шум. Такой выбор размеров опорного импульса и измеряемого фрагмента сигнала обеспечивает значение разности начальных фаз основной гармоники равным около 2,5 - 2,9 радиана.

Из выражения (1) следует, что для k  модулирующих частот, имеющих по p порядков функций Бесселя, получится (2 p+1)^k комбинационных частот.  Таким образом, даже для процессора с тактовой частотой 2 ГГц вычисление  амплитуд и частот комбинационных гармоник становится довольно сложной задачей. Хотя в выражении (1) оператор суммирования формально выполняется для индексов от минус бесконечности до плюс бесконечности, поскольку по определению β≤π, то в реальных вычислениях, значения функции Бесселя с увеличением порядка быстро убывают. Поэтому, учитывая только слагаемые по модулю больше 0.01, для суммирования достаточно пяти членов с порядками -4, -2,0,2,4.

Нами были проведены модельные расчеты распределения амплитуд комбинационных частот.

Исходный опорный импульс имел следующие параметры: количество точек отсчета 64, количество точек отсчета с нулевой амплитудой 1, высота первой ступени 1, D= 0.8516. В качестве модельного сигнала использовался полином второго порядка с коэффициентами 1, 1, -1. К этому сигналу добавлялся случайный, нормально распределенный шум с нулевым математическим ожиданием и дисперсией 0,2. Спектр шума на интервале существования, то есть в течение длительности второго импульса, равной Т_и/2, представлен на графике (рис.2). Полученный в результате импульс представлен на рис. 3.

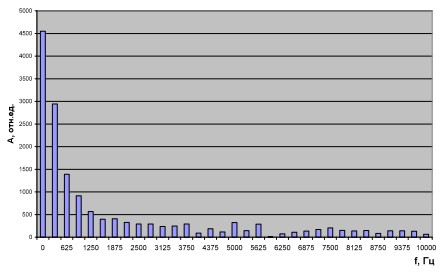
Рис. 2. Спектр зашумленного сигнала

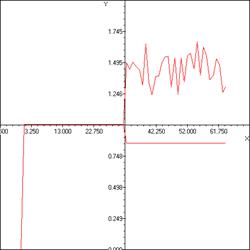
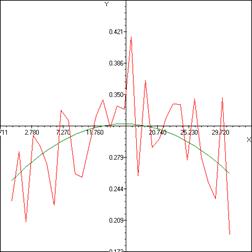
 а)        б)

Рис. 3. Графики: а) опорного импульса с добавленным фрагментом сигнала с шумом в четвертом квадранте показана исходная вторая ступень опорного импульса, б) полезного сигнала (серая линия) и добавленного шума (красная линия).

 Вычисленная начальная фаза основной гармоники опорного импульса равнялась -1.22955727604695, а начальная фаза этой же гармоники для опорного импульса с фрагментом сигнала без шума равнялась 1.3131183875097. Таким образом, разность фаз составила -2.54267566355665.  При добавлении шума начальная фаза основной гармоники становится равной 1.35917893369518. На рис.4 показан график первой производной с нанесенными точками, соответствующими: слева опорному импульсу, справа - импульсу с добавленным сигналом. Как видно из рисунка, точки расположены максимально близко к концам квазилинейного участка зависимости фазы от параметра  D.  Рассчитанные по соотношению (1) комбинационные частоты и амплитуды приведены на рис. 4.

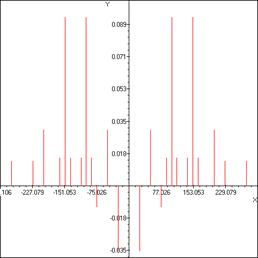
Рис. 4. График комбинационных частот, полученных при фазовой модуляции опорного импульса

Для описанной модели количество комбинационных  гармоник оказалось равным шести. В таблице 1 приведены значения фаз и частот модулирующих гармоник, в таблице 2 рассчитанные комбинаторные частоты и амплитуды.

Таблица 1. Значения фаз и частот модулирующих гармоник

Таблица 2. Рассчитанные комбинационные частоты и амплитуды

На рисунке 5 представлен результат применения описанного фильтра к зарегистрированному кардиоимпульсу. Как видно из рисунка, примененная фильтрация позволила заметно улучшить качество записи.

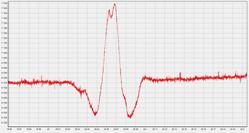
А)

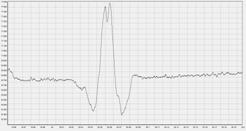
Б)

Рис.5. Кардиоимпульс а) зарегистрированный; б) после обработки описанным алгоритмом

Таким образом, полученные результаты модельных расчетов подтверждают правильность предложенного алгоритма расчета параметров опорного импульса и правил отбора комбинационных частот, появляющихся при фазовой модуляции.

Библиографическая ссылка