Корпус барабана котельной установки является одним из наиболее ответственных элементов, в конструкции которого большое количество продольных и кольцевых сварных швов и штуцерных соединений. Появление трещин в барабанах в процессе эксплуатации вызывается рядом причин. Основными причинами являются: высокий уровень действующих напряжений термосилового происхождения, циклический характер которых обусловлен режимами пуска и останова, а также низкая деформационная способность материала корпуса барабана. Трещины тепловой усталости наиболее часто появляются возле отверстий опускных и питательных труб экранов, около штуцерных соединений из-за местного охлаждения стенок барабана. Для сварных узлов максимальные напряжения достигаются в зоне перехода сварного шва к основному металлу. В ряде работ экспериментально показано, что при циклических испытаниях сварных образцов из углеродистых и низколегированных сталей средней и повышенной прочности в зоне перехода сварного шва к основному металлу реализуются условия «жесткого» нагружения. Исследования Н.А. Махутова, А.П. Гусенкова и др. подтвердили отмеченную закономерность для натурных конструкций. Это обстоятельство позволяет использовать для прогнозирования долговечности сварных соединений единую методику. В работе [2] была предложена и апробирована методика, корректно учитывающая особенности, обусловленные наличием сварных швов. Для расчета допустимого числа циклов используется выражение:
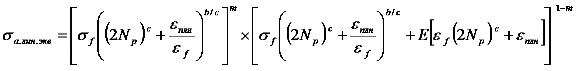
где ![]() - амплитуда напряжений в зоне концентрации (находят в предположении упругого деформирования во всем диапазоне изменения деформаций); Е - модуль упругости; m - показатель, зависящий от условий нагружения, принимает значения от 0 до 1; εпл.н - амплитуда неповреждающей пластической деформации, представляющей деформационный предел усталости. Установлены следующие значения параметра m: m=1 - для напряжений силового происхождения, равномерно распределенных по сечению; m≤0,66 - для напряжений силового происхождения, неравномерно распределенных по сечению (например, изгиб); m≤0,5 - для надрезов, находящихся под влиянием силовой или деформационной нагрузок; m=0,1 - для напряжений деформационного происхождения, в том числе температурных напряжений; m = 0 - для напряжений деформационного происхождения, равномерно распределенных по сечению.
- амплитуда напряжений в зоне концентрации (находят в предположении упругого деформирования во всем диапазоне изменения деформаций); Е - модуль упругости; m - показатель, зависящий от условий нагружения, принимает значения от 0 до 1; εпл.н - амплитуда неповреждающей пластической деформации, представляющей деформационный предел усталости. Установлены следующие значения параметра m: m=1 - для напряжений силового происхождения, равномерно распределенных по сечению; m≤0,66 - для напряжений силового происхождения, неравномерно распределенных по сечению (например, изгиб); m≤0,5 - для надрезов, находящихся под влиянием силовой или деформационной нагрузок; m=0,1 - для напряжений деформационного происхождения, в том числе температурных напряжений; m = 0 - для напряжений деформационного происхождения, равномерно распределенных по сечению.
Для определения параметров σf, εf используются следующие зависимости:
![]() и
и ![]() ,
,
где σв, ψ - предел прочности и относительное сужение при разрыве.
Коэффициенты b и c - тангенсы углов наклона прямых, описывающих в логарифмических координатах зависимость соответственно амплитуды упругой и пластической деформации от разрушающего числа циклов N. В работах С. Мэнсона, Морроу и других авторов показано, что показатели степени с и b для сталей имеют близкие значения (b = -0,12 и c=-0,6). Если рассматриваемый цикл асимметричен, то эквивалентная амплитуда цикла корректируется коэффициентом влияния асимметрии цикла [4]:
![]() ,
,
где a - коэффициент влияния асимметрии цикла; ![]() - амплитуда напряжений цикла, рассчитанная по закону Гука.
- амплитуда напряжений цикла, рассчитанная по закону Гука.
Коэффициент влияния асимметрии цикла находят из выражения:
![]() ,
,
где σmax и σa - соответственно максимальное напряжение цикла и амплитуда напряжений после перераспределения вследствие пластического деформирования. Значения коэффициента a во всех случаях, когда a менее 1, принимают равным 1. Амплитуду напряжений цикла ![]() вычисляют по формуле Губера-Мизеса-Генки. Максимальное напряжение цикла и амплитуду напряжений, соответствующих переходу материала в пластическое состояние, определяют по формуле, являющейся совместным решением уравнений Морроу и Нейбера [2; 4]:
вычисляют по формуле Губера-Мизеса-Генки. Максимальное напряжение цикла и амплитуду напряжений, соответствующих переходу материала в пластическое состояние, определяют по формуле, являющейся совместным решением уравнений Морроу и Нейбера [2; 4]:
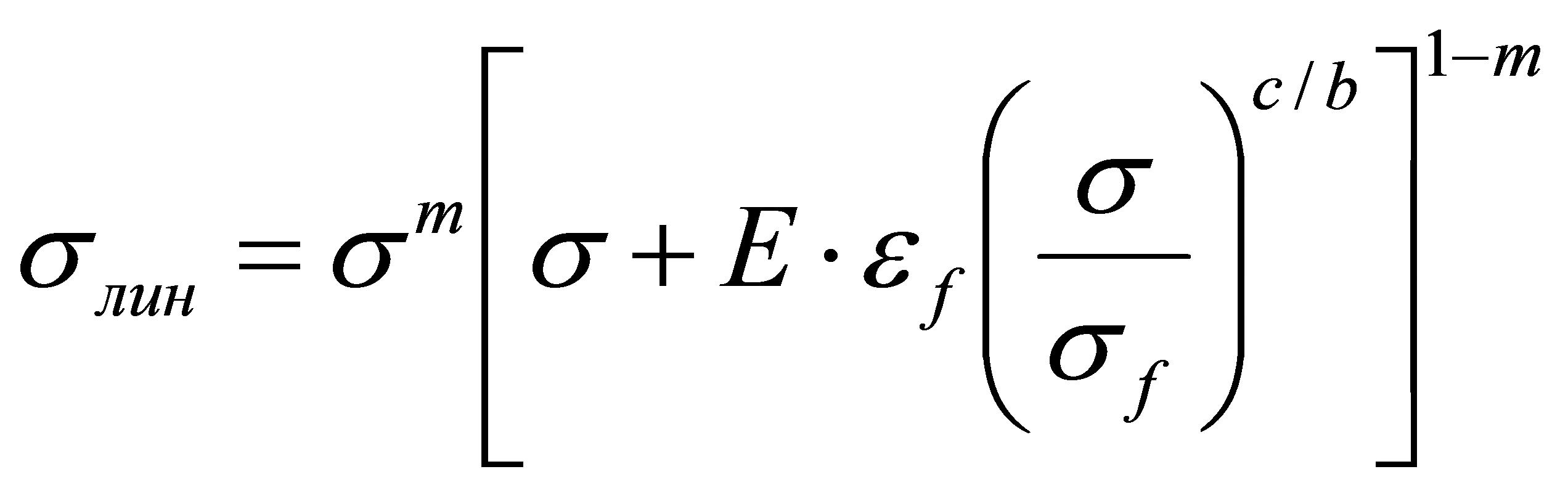
Учет влияния остаточных сварочных напряжений в предлагаемой методике прогнозирования долговечности производим за счет корректировки коэффициента влияния асимметрии цикла.
Для расчета остаточных напряжений из сборной модели рассматриваемого объекта выделяем зоны сварных соединений (рис. 1). Важным моментом является сохранение сетки КЭ для зоны сварного соединения, полученной в результате разбиения общей модели. Это позволяет вычислять сварочные напряжения для узлов сетки КЭ, в которых рассчитаны эксплуатационные напряжения.
Расчет остаточных сварочных напряжений включает вычисление температуры при нагреве и охлаждении в процессе сварки, а также определение напряженно-деформированного состояния сварного соединения. Расчетная модель включает элементы, составляющие сварочный шов, геометрические размеры которых определялись размерами сварочной ванны. Решение осуществляется в трехмерной постановке с использованием метода конечных элементов, реализованного в современных CAE-комплексах. Движение источника тепла при сварке и протяженность сварного шва при моделировании учитывается за счет последовательных тепловложений по длине шва. При этом используются граничные условия теплообмена I рода, отражающие изменение температуры сварочной ванны. Время подвода тепла на каждом участке соответствует времени прохождения данного расстояния электродом в процессе сварки. При расчетах напряженно-деформированного состояния использовали модель упругопластического деформирования с условием пластичности Мизеса. При моделировании процесса упругопластического деформирования задавались кривые механических испытаний, характеризующие свойства стали в зоне шва, зоне термического влияния и остальной части детали в зависимости от температуры. Изменение напряженно-деформированного состояния соединения в процессе сварки не рассматривалось, так как формирование остаточных сварочных напряжений начинается с момента приобретения разупрочненным материалом упругих свойств, то есть с момента остывания конструкции. Максимальное напряжение цикла с учетом остаточных сварочных напряжений находим в результате сложения эксплуатационных и остаточных напряжений.
Для оценки вклада остаточных деформаций и усталостной составляющей в процесс накопления повреждений использовалась гипотеза линейного суммирования повреждений в виде:
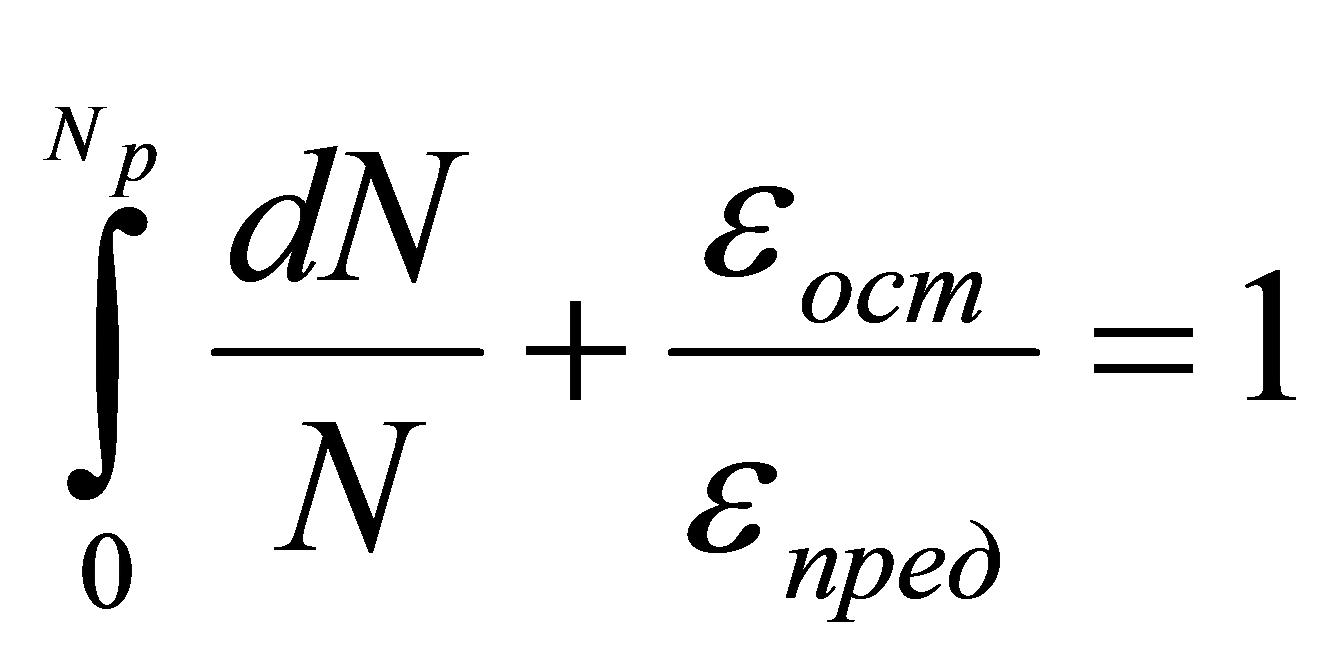 ,
,
где εпред - предельная пластическая деформация; εост - остаточные сварочные деформации; N - допустимое число циклов, определяемое при заданном размахе амплитуды напряжений; Np - количество циклов до появления трещины.
Методика учитывает изменение механических свойств материала при повышенных температурах. Для этого при расчете в модель долговечности вводятся значения данных параметров, соответствующие эффективной температуре цикла, которая определяется выражением [4]:
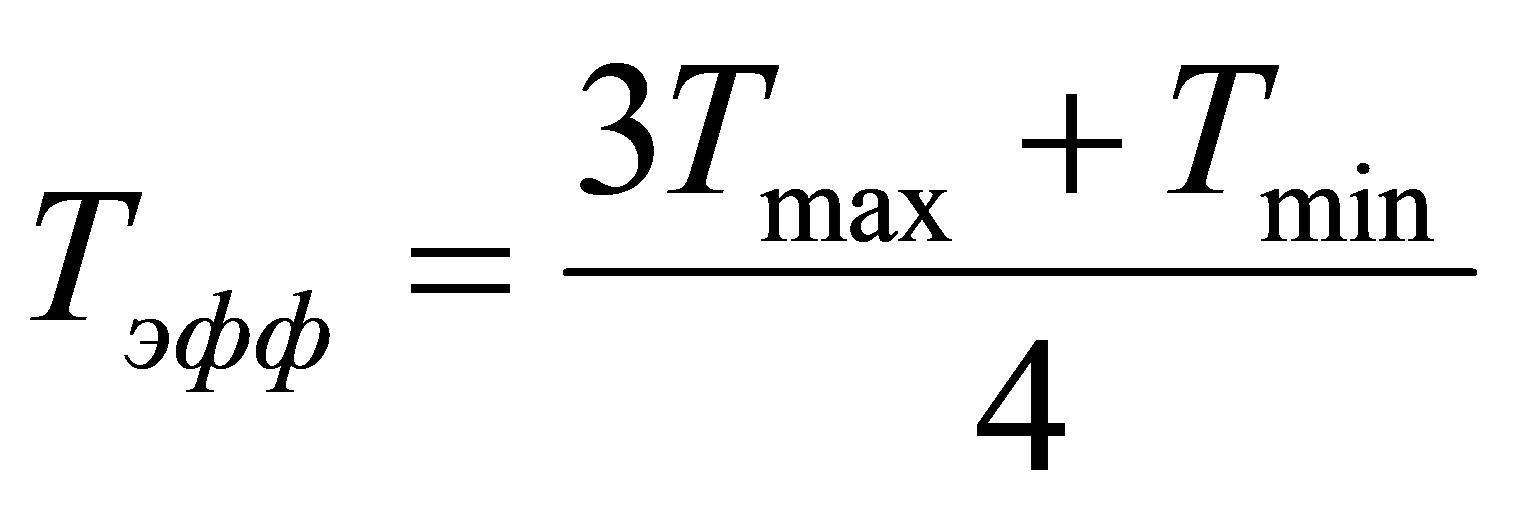 ,
,
где Tmax - максимальная температура цикла; Tmin - минимальная температура цикла.
Свою прикладную реализацию предлагаемая методика получила при оценке долговечности сварного корпуса барабана котла фирмы «Борзиг», функционирующего на одном из предприятий Владимирской генерирующей компании. Его твердотельная модель представлена на рис. 1.
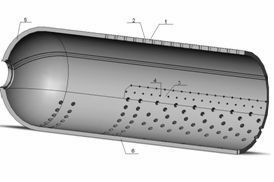
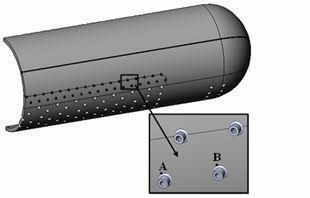
Рис. 1. Твердотельная модель барабана и схема расположения зон контроля температуры.
Модель состоит из зон основного материала, зон термического влияния и зон сварного шва. Зона сварного шва выполнена по ГОСТ 2601-84 [25], диаметр оболочки 1500 мм, общая длина барабана 8200 мм, толщина стенки на линейном участке 60 мм, в местах обечаек 90 мм. Основная задача численного исследования - анализ термонапряженного состояния цилиндрического корпуса при пуске и останове, определение значений величин амплитуд напряжений и последующая оценка долговечности. Решение проводилось в трехмерной постановке. Конечно-элементная модель барабана состояла из 227 945 узлов и 1 100 027 элементов, со сгущением в зонах термического влияния и области сварного шва, что позволило с высокой точностью описать ее геометрию и получить низкую расчетную погрешность. При решении нестационарной задачи теплопроводности использовались граничные условия теплообмена III рода. При определении граничных условий теплообмена учитывались следующие факторы:
- теплообмен в верхней части барабана, обусловленный пленочной конденсацией насыщенного пара на внутренней поверхности;
- теплообмен в нижней части барабана, обусловленный вынужденной конвекцией воды при температуре насыщения;
- теплообмен в зоне подвода питательных труб, зависящий от температуры, скорости движения и давления питательной воды.
Для расчета граничных условий теплообмена использовались данные из пусковой ведомости котла. Для определения начальных условий нестационарной задачи теплопроводности, отражающей процесс вывода котла на эксплуатационный режим после розжига горелок, решали стационарную задачу теплопроводности, моделирующую тепловое состояние барабана при заполнении его водой, имеющей температуру 60 °С. Условия моделирования также отражали останов котла в соответствии правилами эксплуатации паровых и водогрейных котлов. Результаты решения нестационарной задачи теплопроводности, моделирующей изменение теплового состояния корпуса барабана при выводе котла на эксплуатационный режим, показали, что температурное поле корпуса в процессе прогрева в целом достаточно однородно. На рис. 2 отражено тепловое состояние цилиндрического корпуса на 120 и 240 минутах прогрева.
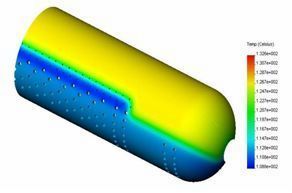
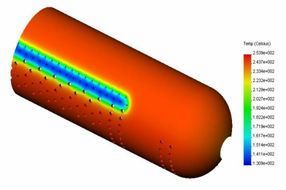
а б
Рис. 2. Тепловое состояние цилиндрического корпуса на 120 (а) и 240 (б) мин прогрева.
Анализ результатов расчета показывает, что максимальные температурные градиенты появляются в области отверстия под люк в начале прогрева, что обусловлено большей толщиной стенки оболочечного корпуса, и в зоне подвода питательной воды, что связано с интенсификацией теплообмена в питательных трубах и значительной разницей между температурой питательной воды и температурой насыщения для рабочего давления.
Изменение температуры на наружной и внутренней поверхности корпуса в точках 1 и 4 приведены на рис. 3.
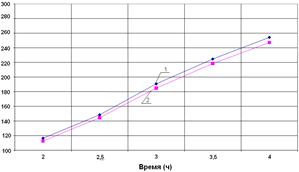
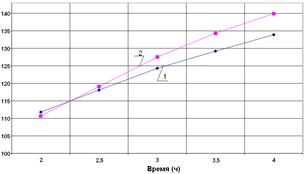
Рис. 3. Изменение температуры (°С) на наружной и внутренней поверхности корпуса в контрольных точках 1 и 4.
Давление, действующее в корпусе барабана, изменяется за время пуска от 0 до 42 атм. Для выбранных временных шагов производится расчет напряженно-деформированного состояния в рамках теории упругости, реализованной для метода конечных элементов.
В пусковой ведомости котла приведены значения расширения корпуса барабана, зафиксированные при пуске контрольными реперами. При выходе на эксплуатационный режим котла, когда давление достигает рабочей величины, расчетные и реперные значения осевого расширения близки, и разница составляет 3%. Малая величина расхождения при выходе на эксплуатационный режим позволяет говорить о корректности выбранных граничных условий. Результаты расчета с помощью МКЭ показывают, что наиболее напряженной является зона ввода питательной воды и отверстий опускных труб. Именно в этих местах наблюдаются максимальные значения локальных показателей НДС. На рис. 4 показаны зоны концентрации напряжений на модели корпуса в зоне подвода питательной воды и опускных труб. В таблице 1 приведены основные результаты исследования напряженного состояния.
Таблица 1 - Результаты расчета напряженного состояния корпуса в местах концентрации напряжений
|
Зона ввода питательной воды |
|
||||||||||
|
№ узлов |
σx, МПа |
σy, МПа |
σz, МПа |
τxy, МПа |
τyz, МПа |
τzx, МПа |
σ1, МПа |
σ2, МПа |
σ3, МПа |
||
|
178955 |
499,2 |
24,3 |
36,9 |
-0,1 |
2,7 |
-11,1 |
498,2 |
43,3 |
17,8 |
||
|
178771 |
504,9 |
24,8 |
42,5 |
5,8 |
3,5 |
-8,7 |
505,0 |
46,1 |
21,1 |
||
|
178582 |
502,2 |
25,1 |
39,6 |
1,8 |
-2,3 |
-10,1 |
502,2 |
44,9 |
19,9 |
||
|
Зона опускных труб |
|||||||||||
|
№ узлов |
σx, МПа |
σy, МПа |
σz, МПа |
τxy, МПа |
τyz, МПа |
τzx, МПа |
σ1, МПа |
σ2, МПа |
σ3, МПа |
||
|
486 |
-184,3 |
-22,4 |
-50,8 |
29,3 |
9,2 |
-87,7 |
-5,5 |
-19,7 |
-232,1 |
||
|
43293 |
-179,8 |
-14,2 |
-44,4 |
25,5 |
8,0 |
-88,5 |
-1,9 |
-19,5 |
-218,0 |
||
|
2213 |
-169,7 |
-18,3 |
-37,6 |
23,4 |
6,4 |
-79,1 |
-6,0 |
-13,4 |
-226,0 |
||
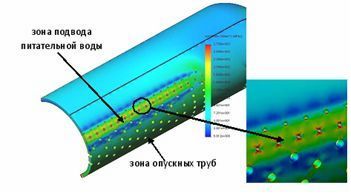
Рис. 4. Поле напряжений в зоне отверстий подвода питательной воды и опускных труб.
Анализ напряжений, приведенных в таблице 1, показывает, что максимальные их значения превышают напряжения, соответствующие пределу текучести σ0.2 материала, то есть реализуется процесс циклического упругопластического деформирования.
Для определения уровня остаточных сварочных напряжений в штуцерном соединении (рис. 1) выполнено расчетное моделирование процесса сварки. Граничные условия определялись на основании работ [3; 5]. При решении учитывалось влияние температуры на физико-механические свойства металла шва и основного металла. Максимальные значения остаточных напряжений в радиусе перехода сварного шва к основному металлу составили 280-300 МПа.
Для расчетной оценки долговечности использовались физико-механические характеристики материала (стали 22К), приведенные к эффективной температуре цикла нагружения. Эффективная температура цикла принята Тэфф = 200 °С. Постоянные модели долговечности имели следующие значения: εf = 0,33, m = 0,5, b = -0,12, c = -0,6, σf = 780.
Для определения влияния уровня остаточных сварочных напряжений на долговечность корпуса проведено расчетное исследование с вариацией величины эквивалентной амплитуды напряжений в диапазоне изменения σа=400-100 МПа. По результатам расчетов построены кривые, приведенные на рис. 5.
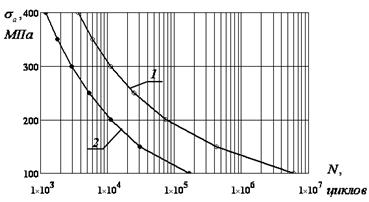
Рис. 5. Влияние остаточных сварочных напряжений на долговечность корпуса барабана: 1 - эксплуатационные напряжения; 2 - с учетом сварочных напряжений.
Расчетное значение долговечности, то есть количество циклов до образования трещины для штуцера, расположенного в зоне подвода питательной воды с учетом сварочных напряжений составило ![]() циклов.
циклов.
Максимальная расчетная величина остаточной сварочной деформации (εост ) составила 4,3·10-3. Величина предельной пластической деформации -0,69. Таким образом, вклад остаточной деформации в общую повреждаемость штуцерного соединения, согласно гипотезе линейного суммирования повреждений, не превышает 0,0062, то есть может не учитываться.
По данным [1], корпуса барабанов промышленных котлов при нормативных условиях пуска при хорошем водном режиме и мерах по предупреждению стояночной коррозии способны выдержать более 3000 пусков и остановов без появления трещин. Учитывая, что в данной работе моделировали штатные условия пуска и останова, можно считать, что полученные данные по оценке долговечности сварного барабана не противоречат опыту эксплуатации. Очевидно, что без учета влияния сварочных остаточных напряжений используемая методика дает завышенные результаты при оценке ресурса.
Рецензенты:
- Гоц А.Н., д.т.н., профессор кафедры тепловых двигателей и энергетических установок ФГБОУ ВПО «Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых», г. Владимир.
- Кульчицкий А.Р., д.т.н., профессор, заместитель главного конструктора по испытаниям ООО «ВМТЗ».
Библиографическая ссылка
Рассолов Т.В., Аборкин А.В., Иванченко А.Б. ВЛИЯНИЕ ОСТАТОЧНЫХ СВАРОЧНЫХ НАПРЯЖЕНИЙ НА УСТАЛОСТНУЮ ДОЛГОВЕЧНОСТЬ УЗЛОВ КОТЕЛЬНЫХ УСТАНОВОК // Современные проблемы науки и образования. 2011. № 6. ;URL: https://science-education.ru/ru/article/view?id=5070 (дата обращения: 17.02.2026).



