В промышленности, в качестве отделочно-упрочняющей обработки различных деталей, находит применение поверхностное пластическое деформирование (ППД) роликами. Деформирующий элемент в инструменте для обработки ППД может быть выполнен в виде шара, ролика с цилиндрической, конической или криволинейной (профильной) поверхностями. Применение конических роликов позволяет получить удлиненный, так называемый каплевидный, контакт, который обеспечивает наилучшие показатели обработки.
Несмотря на то, что конические ролики применяются на практике давно, вопросы, касающиеся нахождения фактических количественных параметров контактной зоны, ее площади раскрыты не полностью.
Для определения зависимости параметров контакта от изменения глубины внедрения ролика в поверхность заготовки в настоящей работе рассмотрен контакт обрабатываемой заготовки, представляющей собой цилиндр с радиусом образующей Rд, с деформирующим роликом - усеченным конусом с радиусом меньшего основания rрmin, радиусом закругления на начальном участке R1 и углом конуса θ. При этом условно принималось, что вокруг деформирующего ролика отсутствует волна вытесненного металла.
Вид отпечатка, получаемого при внедрении ролика в деталь, можно получить экспериментально путем проведения статического вдавливания (рис. 1, а) или при помощи булевой операции вычитания при моделировании контакта в среде любой CAD-системы трехмерного моделирования (рис.1, б). Очертания контурной линии контакта при этом имеют явно выраженную эллипсовидную форму.


а) б)
Рис. 1. Отпечаток на цилиндрической детали от вдавливания конического ролика полученный: а - при натурном эксперименте, материал заготовки алюминий, усилие 10 кН;
б - при моделировании контакта в среде программы твердотельного моделирования.
Для нахождения полуосей эллипсов, частями которых очерчена контурная линия контакта, угол самоподачи принят равным нулю, так как он мало влияет на размеры контакта и является незначительным по величине (не более 1.5...2 град.). Контурная линия контакта расположена на поверхности детали, а ее крайними точками являются точки Б, В, Г и Д (рис. 2).
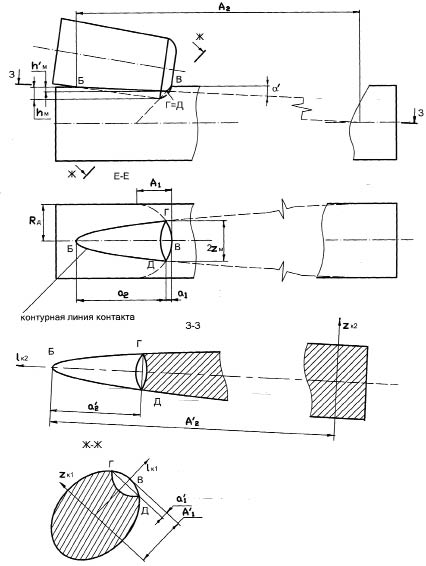
Рис. 2. Схема к определению полуосей эллипсов представляющих контурную линию контакта
Проведя секущую плоскость по точкам Г, В и Д получен эллипс с полуосями А1 и Rd. Аналогично плоскость проходящая через точки Г, Б и Д дает эллипс с полуосями А2 и Rd. Уравнения эллипсов имеют вид:
![]() ;
; ![]() , (1)
, (1)
Решение уравнений (1) для условий, когда ![]() дает выражения для определения больших полуосей АI1 и АI2:
дает выражения для определения больших полуосей АI1 и АI2:
![]() ;
;
![]() (2)
(2)
где а11 и а21 - длины контакта в рассматриваемых плоскостях, определяемые по формулам:
![]() ;
; ![]() ;
;
![]()
Проекции найденных по формулам (2) полуосей эллипсов на плоскость параллельную поверхности детали и проходящую через точки Г и Д равны:
![]() ;
; ![]() (3)
(3)
После преобразований получены выражения для определения полуосей эллипсов через геометрические параметры контактирующих тел и контактной зоны для участков:
Внедрения ![]() (4)
(4)
Сбега ![]() (5)
(5)
Длины участков внедрения и сбега, а также полуширина контакта входящие в формулы (1, 2) выражаются через максимальную глубину внедрения деформирующего ролика, размеры детали, ролика и углов их относительного расположения. Для их определения рассмотрено сечение Б-Б (рис. 2), в котором ролик представляет собой эллипс с полуосями rz и ry , а заготовка окружность с радиусом Rд.
Их уравнения в системе координат с началом в центре сечения ролика имеют вид:
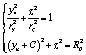 (6)
(6)
где С, rz и ry определяются по формулам:
![]() ;
;
![]()
![]()
Совместное решение уравнений (6) при yк=hм, z=zм позволяет получить биквадратное уравнение вида:
![]() (7)
(7)
где E1 и Е2 определяются по формулам:
![]() ;
; ![]() .
.
Решив уравнение (7) получено выражение для определения полуширины контакта, которое после упрощения имеет вид:
![]() (8)
(8)
Длина участка внедрения определяется из треугольника OMD (рис. 3):
![]() (9)
(9)
Вторая составляющая длины контакта определена из выражения, полученного решением геометрической задачи при рассмотрении сечения А-А (рис. 3), в котором контурная линия детали представляет собой эллипс с уравнением имеющим вид:
![]() (10)
(10)
Подставив в это уравнение координаты точки выхода ролика из контакта с деталью, получено квадратное уравнение, решение которого позволяет получить выражение для определения длины участка сбега контакта:
![]() ,
, ![]()
![]()
![]() (11)
(11)
где α - задний угол внедрения ролика; ω - угол самозатягивания.
Площадь контакта, исходя из определенных геометрических параметров (4, 5, 8, 9, 11), будет находиться из выражения:
![]() (12)
(12)
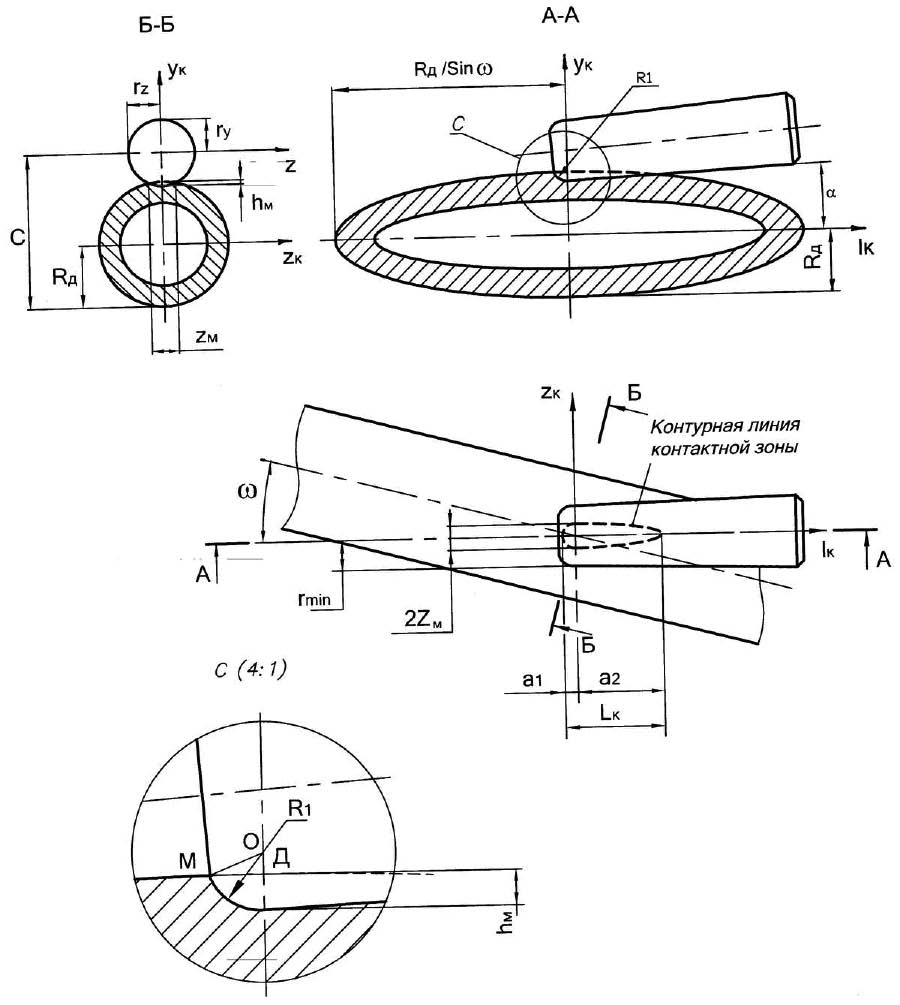
Рис. 3. Схема к определению геометрических параметров контурной линии контакта
Сравнение площади контакта полученной расчетом по полученной зависимости (12) и при компьютерном моделировании в среде системы твердотельного моделирования T-Flex CAD 3D (рис. 4) показывает, что расхождение результатов не превышает 3% при глубинах внедрения до 0,1 мм.
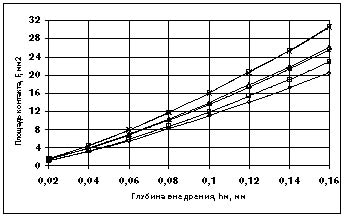
Рис. 4. Зависимость площади контакта от глубины внедрения ролика: 1,2,3 - полученная по формуле (12); 4,5,6 - полученная на основании компьютерного моделирования, для деталей диаметром 10, 20 и 35мм соответственно, rpmin=8,75мм, R1=2мм,ω=1,5°, α=1,5°, θ=2°.
Таким образом, предложенная методика может быть применена на практике для назначения режимов обработки при ППД коническими роликами.
Библиографическая ссылка
Никифоров Н.И. ОПРЕДЕЛЕНИЕ ПЛОЩАДИ КОНТАКТА ПРИ ППД КОНИЧЕСКИМИ РОЛИКАМИ // Современные проблемы науки и образования. 2010. № 4. ;URL: https://science-education.ru/ru/article/view?id=4514 (дата обращения: 24.02.2026).



