Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы

Мялицин А.В.

На основании закона сохранения массы вещества, экспериментальных исследований и принятых допущений составлено математическое описание процесса сушки древесины в камерах непрерывного действия туннельного типа. Приведены решения полученных уравнений и соответствующие выводы. Ключевые слова: сушка древесины, камеры непрерывного действия, теплообмен, массообмен

Статья в формате PDF

168 KB

Ранее уже предпринимались попытки анализа процессов тепло- и массообмена для камер непрерывного действия [1, 2]. Была получена следующая система уравнений, описывающих процесс тепло- и массообмена в туннельной сушилке:

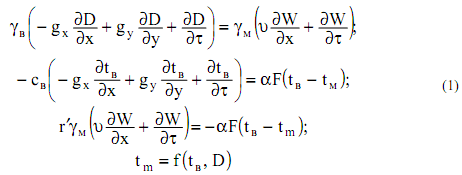
с начальными и граничными условиями:

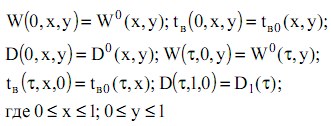
Решение системы (1) в операторном виде выглядит следующим образом:

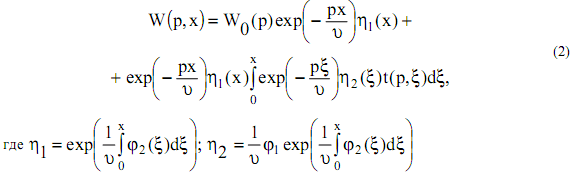
Первое слагаемое в (2) показывает влияние возмущения по начальной влажности материала на влажность материала в любом сечении по длине сушилки, а второе слагаемое учитывает влияние распределенного по длине возмущения параметров сушильного агента на влажность материала в сушилке.

В (1) - (2) приняты следующие обозначения:

x, y, z - координаты соответственно по длине, высоте и ширине сушильной камеры, м;

g(x), g(y) - расход воздуха, соответственно, по оси x и y, м³/ч;

F - площадь поверхности высушиваемого материала, приходящаяся на единицу объема сушильного пространства, м²/м³;

- скорость перемещения материала по оси x, м/ч;

γ_в, γ_м - плотность, соответственно, воздуха и материала, кг/м³;

t_в, t_м, t_m - температура воздуха, поверхности материала и мокрого термометра, °С;

α - коэффициент теплоотдачи, Вт/м²°С;

W - влажность материала, кг/кг;

с_в, с_м - теплоемкость воздуха и материала, Дж/кг°С;

D - влагосодержание воздуха, кг/кг.

Таким образом, полученное решение (2) описывает искомые распределения по длине камеры, однако, его практическое применение представляется весьма затруднительным по следующим причинам:

1. Выражение (2) для практического применения необходимо привести из операторной формы в нормальную, а для этого надо знать параметры η₁, η₂, φ₁, φ₂.
2. Определение указанных параметров эмпирическим путем также не представляется возможным т.к. мы не знаем их физический смысл, а авторы [1, 2] никак это не комментируют.

Поэтому очевидна необходимость построения достаточно простой математической модели камеры непрерывного действия, пригодной для инженерных расчетов.

Математическое описание камеры непрерывного действия основано на законе сохранения массы вещества и дополнено экспериментальными данными. При создании математического описания камеры в соответствии со специфическими свойствами и условиями сушки древесины нами приняты следующие допущения:

1. пиломатериал входит в камеру и выходит из нее непрерывно со скоростью, установленной в соответствии с выбранным режимом сушки

2. в поперечном сечении камеры параметры сушильного агента распределены равномерно;

3. отношение массы влаги к рассматриваемому объему пиломатериала считаем удельным влагосодержанием

Функция удельного влагосодержания древесины в любом сечении камеры зависит от времени и координаты Сформулируем специфические особенности, определяющие закономерность процесса сушки в камере непрерывного действия.

Выделим в камере сечением x₁, x₂ участок и в рассматриваемом объеме штабеля пиломатериала определим количество содержащейся влаги в момент времени

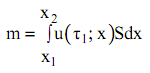                          (3)

Количество влаги в момент времени на этом участке

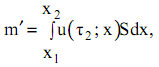                                              (4)

где S - площадь пиломатериала в рассматриваемом сечении штабеля.

Во время процесса сушки можно изменить влажность пиломатериала и параметры сушильного агента. Поток влаги через сечение камеры с течением времени меняется. За промежуток времени , через сечение x₁ проходит следующее количество влаги, перемещающееся вместе со штабелем с определенной скоростью движения, установленной режимом сушки:

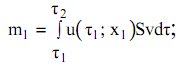                      (5)

через сечение x₂ за тот же промежуток времени выходит количество влаги:

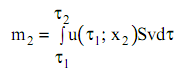                       (6)

В результате воздействия сушильного агента на древесину из нее выделяются пары влаги. Интенсивность их выделения - сложная функция свойств пиломатериала, параметров сушильного агента и ряда других факторов процесса сушки

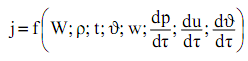
В свою очередь, входящие сюда зависимости - функция координаты и времени, т. е.  Эту функцию определяют из экспериментальных данных, полученных путем непрерывного взвешивания контрольного пакета пиломатериала (при заданных условиях сушки) в каждой зоне нахождения штабеля, где одновременно измеряются все параметры агента - температура, относительная влажность и скорость. Зная влагосодержание (исходное и конечное) на любом участке камеры, можно определить интенсивность испарения влаги из древесины на каждом участке за промежуток времени

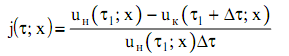                                  (7)

Количество испарившейся влаги на участке x₁, x₂ за промежуток времени τ₁, τ₂

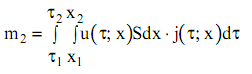                                     (8)

Эта величина зависит от имеющегося количества влаги в рассматриваемом объеме и от параметров сушильного агента.

С помощью выражений (3) - (8) определяют потоки влаги при сушке пиломатериала в камере непрерывного действия.

Составим уравнение интегрального баланса для любого участка камеры. В интегральной форме выражение имеет вид

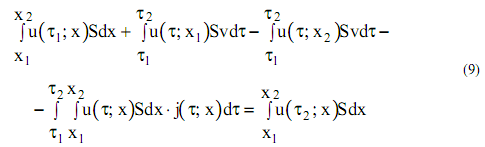                  (9)

Перегруппируем члены уравнения (9), перепишем их в форме приращений и разделим все члены уравнения на . На основании теоремы о среднем получим математическую модель камеры по каналу влагосодержания древесины в дифференциальной форме:

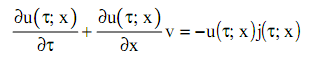                             (10)

Этому уравнению соответствует следующее решение:

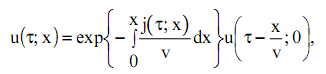                             (11)

где - продолжительность нахождения данного штабеля в камере в соответствии с изменением входящей влажности

Рассуждая аналогично, представим влагосодержание d сушильного агента как количество влаги в объеме абсолютно сухого воздуха. При движении агента через штабеля пиломатериала величина d зависит от температуры и скорости, а последние параметры - от времени и координаты, отсюда d = f(τ, x).

Интенсивность процесса сушки с учетом параметров сушильного агента в камере в зависимости от температуры:

                                (12)

в зависимости от скорости:

                              (13)

где u и d - влагосодержание древесины и сушильного агента;  - коэффициенты насыщения сушильного агента в зависимости от температуры и скорости (определяются из эмпирических зависимостей и экспериментальных данных).

Подставим значения коэффициентов интенсивности (12), (13) в уравнение (9) и на основании предыдущих рассуждений получим математическую модель по каналу влагосодержания сушильного агента в объекте; совместно с уравнением (10) имеем систему уравнений для камеры непрерывного действия:

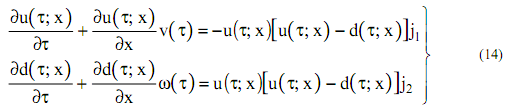
Если в камере установлены регуляторы, тогда коэффициенты интенсивности зависят только от координаты (стационарный режим)

Отсюда систему уравнений (14) можно представить для решения в виде их суммы

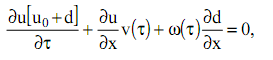                                  (15)

а решение в любой момент времени при   имеет вид

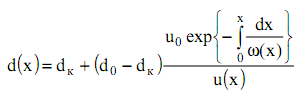                          (16)

Полученное распределение (16) представляет собой достаточное простое, вполне пригодное для инженерных расчетов выражение. Тем не менее, для его эффективного применения нам необходим ряд экспериментальных данных, а именно:

• распределение влажности пиломатериалов по длине камеры;
• распределение скорости циркуляции агента сушки по длине камеры.

Такие данные были нами получены при проведении опытных сушек в Кормовищенском ЛПХ (Пермский край). Эти данные соответствуют моменту окончания процесса сушки, т.е. перед выгрузкой 4-го штабеля из камеры.

После обработки данных эксперимента получены следующие выражения:

- изменение влажности пиломатериалов по длине камеры:

- изменение скорости циркуляции агента сушки по длине камеры:

Выражение (16) для описанного выше момента окончания сушки будет иметь вид:

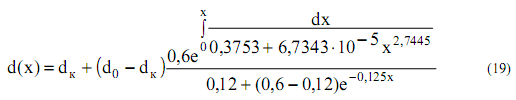
В результате анализа экспериментальных данных было получено распределение влагосодержания по длине камеры:

                                  (20)

При этом d₀=0,042 кг/кг; d_k=0,047 кг/кг. Распределение влагосодержания агента сушки по длине камеры непрерывного действия изображено на рис. 1.

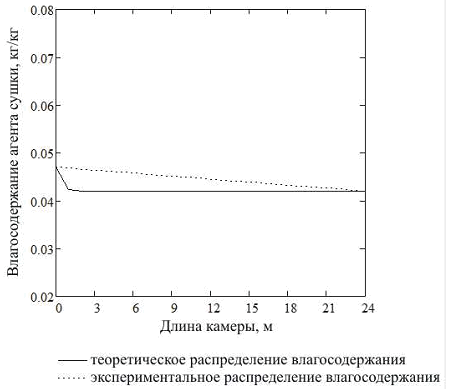
Рис. 1. Распределение влагосодержания агента сушки по длине камеры непрерывного действия

Таким образом, сопоставление данных эксперимента с результатами теоретических расчетов показывает их достаточно близкое совпадение. Несущественные расхождения результатов при этом может быть объяснено некоторыми допущениями при разработке формализованного описания камеры. В первую очередь, это принятие допущения о постоянном движении высушиваемого материала.

СПИСОК ЛИТЕРАТУРЫ

1. Допнер Г.А. Математическое описание процессов тепло- и массообмена в туннельной сушилке [Текст] / Г. А. Допнер, П. В. Ефимов, В. И. Потапов, В. Н. Севастьянов // Лесоинженерное дело и механическая технология древесины. Материалы конференции по итогам научно-исследовательских работ. Сибирский технологический институт, Красноярск. 1969. - С. 301-305.
2. Ефимов П.В. Задача оптимального контроля в системе управления туннельной сушилкой [Текст] / П.В. Ефимов, В.И. Потапов // Лесоинженерное дело и механическая технология древесины. Материалы конференции по итогам научно-исследовательских работ. Сибирский технологический институт, Красноярск. 1969. - С. 306-309.

Библиографическая ссылка