Сетевое научное издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 0,936

Введение

Роль математических знаний в научно-техническом прогрессе и суверенитете России значительна, поэтому правительство требует повысить качество преподавания математики в школе. Однако успехи детей зависят не только от учителя, но и от их индивидуальных особенностей, желания заниматься предметом.

Важной компетенцией, которая формируется при обучении математике, является умение оперировать числами, поэтому для успешного обучения математике необходимы умения, требующие развития «чувства числа». Ученые используют различную терминологию при описании способности к восприятию количественной информации: «чувство числа», «приблизительное чувство числа», «интуитивное чувство числа», или «несимволическое чувство числа» [1, с. 130]. Под «чувством числа» ряд исследователей понимают интуитивную способность оценивать приблизительное количество предметов без счета и отличать большее их скопление от меньшего [2–4]. А как известно, математическую интуицию можно развивать [5].

«В настоящее время “чувство числа” рассматривается как возможный базовый предиктор математических способностей», – отмечает Ю.В. Кузьмина [3, с. 51]. Большинство современных ученых рассматривают его как врожденное начало математического интеллекта [1; 3]. Группа психологов под руководством Д.Халберды выяснила, что дети с хорошо развитым «чувством числа» не испытывают проблем со школьным курсом математики [3]. При этом одни исследования подтверждают, что интуитивное «чувство числа» связано с математическими достижениями, а в других подчеркивается, что значимой связи между ними нет [4; 6; 7].

Нейробиолог Д. Соуза рассматривает «чувство числа» как «биологически опосредованное врожденное качество, которое ограничено простыми интуитивными представлениями о количестве, быстрым и точным восприятием небольших множеств, способностью к сравнению числовых величин и пониманию простых арифметических действий» [7, с. 38]. В данной статье используется более широкое определение понятия «чувства числа». Авторы считают, что в него входит и набор умений, который возникает в результате изучения математики:

– понимание количества и умение использовать для записи обозначающие их символы;

– умение определять приблизительное количество объектов без их счета;

– знание понятий «больше» и «меньше» в контекстах количества и размера;

– понимание отношения между одним объектом и группой объектов (например, что число 6 обозначает группу из шести объектов);

– понимание последовательности чисел в списке;

– умение сравнивать числа;

– умение выполнять простейшие арифметические действия.

Одной из важных компетенций, которая формируется при обучении математике, является умение оперировать числами. Умение обращаться с числами, обнаружение и анализ их сходства и различия, решение задач и применение математических знаний в реальном мире требует освоения определенных алгоритмов. Поэтому учителю необходимо знать и уметь диагностировать развитие «чувства числа» у обучающихся.

Цель исследования – проведение сравнительного анализа развития «чувства числа» у детей младшего школьного возраста и выработка рекомендаций по его формированию.

Материал и методы исследования

Педагогическое исследование проводилось в два этапа: первый этап проходил в 2019–2021 учебные годы, второй этап – в 2023–2025 учебные годы в МОУ «Средняя общеобразовательная школа № 27» г. Саранска. В исследовании принимали участие 49 школьников 2-х и 3-х классов в возрасте 8–10 лет (дети 2011 г. и 2015 г. рождения обучались у одного учителя с разницей в четыре года). Школьники обучались по программе и учебно-методическому комплексу пособий по математике для начальной школы авторского коллектива под руководством М.И.Моро (серия «Школа России»).

В ходе исследования применялся комплекс теоретических и эмпирических методов: анализ и синтез научной и психолого-педагогической литературы, нормативных документов, тестирование и анкетирование обучающихся, сравнительный анализ результатов их деятельности.

Для составления заданий на знание чисел авторы опирались на систему оценки способностей младших школьников разных возрастных категорий, разработанную Ш.Гриффином и Р. Кейсом [7, с.153–155].

Результаты исследования и их обсуждение

Чтобы оценить развитие «чувства числа» у обучающихся начальных классов, авторами было составлено по два варианта тестовых заданий (табл.1).

Таблица 1

Образцы вариантов тестовых заданий

Примечание: составлена авторами на основе полученных данных в ходе исследования

Данная система тестирования, отмечают исследователи, поможет определить учителю, как развивается «чувство числа» у детей, дифференцировать задания, чтобы выровнять уровни компетенции учеников [7, с. 152].

Вопросы уровня 2 рассчитаны на детей 8 лет и были предложены обучающимся во 2-м классе, в конце первой четверти (в 2019 г. и 2023г. соответственно). Вопросы уровня 3 рассчитаны на детей 10 лет. Тест был дан в конце четвертой четверти 3-го класса (в 2021 г. и 2025 г. соответственно).

Обучающиеся 2011 г. рождения приступили к решению всех заданий, два ученика 2015г. рождения не приступили к решению заданий 2, 3б, 4а и 4б. Четверо обучающихся 2011г. рождения написали тест на 100 %, среди детей 2015г. рождения таковых не было. В 2019 г. средний процент правильно решенных заданий составил 83 %, в 2023 г. – 75 %. Таким образом, тестовые задания уровня 2 в 2023 г. были выполнены на 8 % хуже, чем в 2019г. (табл.2).

Таблица 2

Результаты решения заданий уровня 2 (I четверть, 2 класс)

Примечание: составлена авторами на основе полученных данных в ходе исследования

Процент выполненных заданий 3а, 3б, 4б и 5а в обоих классах примерно одинаков и высок. Связано это со стандартной формулировкой вопросов и регулярным решением заданий данного типа. В заданиях уровня 2 формулировка вопросов 2, 5а и 5б, 6 и 7 отличается от принятых в школе. В заданиях уровня 3 нестандартными являются вопросы 2, 3а и 3б, 4а и 4б. Остальные задания являются общепринятыми для уроков математики. Тестирование показало, что дети не были готовы к другой формулировке вопросов: они отвечали на них хуже. Как видно из рис. 1, в 2023 г. процент правильно выполненных заданий уровня 2 ниже или совпадает с 2019 г.

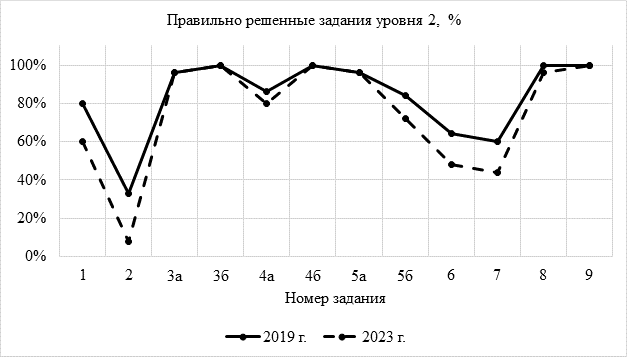
Рис. 1. Результаты решения заданий уровня 2

Примечание: составлен авторами по результатам данного исследования

В задании 1 уровня 2 неправильные ответы были связаны с тем, что ученики не обратили внимание, что число должно стоять левее, а не правее числа 50.

Задание 2 уровня 2 вызвало наибольшее затруднение у школьников. Если в 2019г. 8 обучающихся, что составило 33 % от общего количества детей класса, догадались, что в задаче два ответа (от числа 49 на пять цифр отстоят числа 44 и 54), то в 2023г. году их было всего 2 чел. (8 % от общего количества обучающихся в классе). Следует отметить, что в 2023 г. 64 % детей написали только одно число (93), а 28 % детей сделали задание неверно.

В задании 4 уровня 2 большинство неверных решений связано с тем, что обучающиеся невнимательно прочитали формулировку задания, прочитав слово «меньше» как «больше».

Анализ неверных ответов на задания 5а и 5б уровня 2 говорят о том, что дети не понимают формулировку задания, ошибаются при сравнении чисел. Понятия «больше» и «меньше» для чисел являются для них стандартными, а вот «ближе», «дальше», «левее», «правее» – нет. Неверные ответы на задания 6 и 7 уровня 2 говорят о том, что младшие школьники путают понятия «цифра» и «число».

Подавляющее большинство обучающихся в обоих классах правильно выполнили задания 8 и 9 уровня 2 на сложение и вычитание двузначных чисел. Связано это с тем, что, во-первых, двузначными числами легче оперировать, во-вторых, они часто используются в повседневной жизни и, в-третьих, прошло достаточно времени для усвоения темы.

Анализ выполненных заданий уровня 3 показывает, что в 2025 г. тест был выполнен на 15 % хуже, чем в 2021 г. В 2021 г. 6 чел. выполнили задания уровня 3 на 100 %, в 2023г. – 2 чел. Сводные данные по 3 классу приведены в табл. 3.

Таблица 3

Результаты решения заданий уровня 3 (IV четверть, 3 класс)

Примечание: составлена авторами на основе полученных данных в ходе исследования

Задание 2 уровня 3 выполнено лучше аналогичного задания уровня 2, но количество верных ответов осталось низким и составило всего 16 %. Обучающиеся 3-го класса не вспомнили, что уже выполняли аналогичное задание во 2-м классе. Задания 1, 2 и 7 связаны с вычислением трехзначных чисел. Операции с трехзначными числами даются гораздо сложнее, чем с двузначными. Кроме того, трехзначные числа были изучены сравнительно недавно, поэтому большинству обучающихся пока было трудно оперировать ими. Кроме того, детям нужно гораздо больше времени для усвоения действий с трехзначными числами, чем на это отводит школьная программа [8].

Следует отметить, что средний балл по математике в обоих классах был примерно одинаков (в 2020–2021 учебном году в 3-м классе он составил 4,3; в 2024–2025 учебном году – 4,1), но тестовые задания на «чувство числа» спустя четыре года (обучающимися 2015г. рождения) были выполнены хуже (рис. 2).

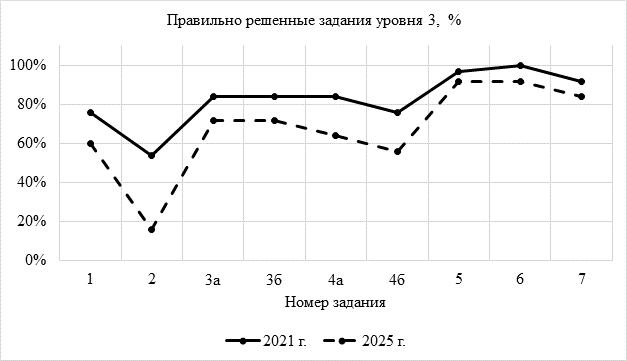
Рис. 2. Результаты решения заданий уровня 3

Примечание: составлен авторами по результатам данного исследования

Таким образом, в исследовании участвовали дети примерно одинакового уровня развития, преподавал у них один учитель, стаж работы которого более 20 лет, но при этом разница в выполнении некоторых заданий – значительна.

Возможные причины ухудшения результатов авторы связывают с содержанием школьной программы по математике: в начальной школе она регулярно усложняется, а количество часов уменьшилось с 6 до 4 [8]. Увеличилось количество детей, испытывающих трудности с выполнением арифметических операций, запоминанием правил. Порядка 25 % обучаемых класса не понимают сути операций «вычитание», «умножение», возникают сложности с восприятием трехзначных (и, как следствие, многозначных) чисел.

Кроме того, существует проблема, связанная с нарастающим ухудшением здоровья обучающихся. Исследователи отмечают, что более 90 % детей в России имеют различные отклонения в состоянии здоровья [9, с.12]. В школах растет число детей с дислексией, дисграфией и дискалькулией [10; 11]. Важна и проблема развития памяти школьника [12–14].

Большинство исследователей признают, что формальное и неформальное образование может развить «чувство числа» еще в дошкольные годы [4; 7]. Безусловно, родители играют здесь ключевую роль. Ученые считают: чтобы помочь детям развить их математические способности, учитель должен уделять приоритетное внимание развитию «чувства счета» и показывать связь между школьной математикой и повседневной жизнью [15]. О.М.Коржачкина обосновывает необходимость решения арифметических задач разного уровня сложности на всех этапах обучения математике в средней школе. По ее мнению, это способствует развитию «чувства числа», которое придает гибкий и концептуальный характер формируемому у обучающихся математическому типу мышления [16].

Приведем некоторые рекомендации, которые необходимо использовать при обучении математике и развитии «чувства числа» у детей младшего школьного возраста (некоторые из них могут быть выполнены с помощью родителей):

1. Считайте и группируйте объекты, делите их на большие и небольшие группы, проводите внутри этих групп вычисления.

2. Комбинируйте группы, тренируйтесь в сложении и умножении, сопоставляйте символы числа с их количественными значениями.

3. Сравнивайте количества с помощью палочек, используйте слова «больше чем» и «меньше чем».

4. Тренируйтесь оценивать приблизительное количество, задавайте вопросы о приблизительном количестве чего-либо в повседневных диалогах, используйте формулировки «примерно сколько» или «как много».

5. Обсуждайте понятия «время», «расстояние», «деньги». Задайте вопрос: «Сколько времени требуется, чтобы дойти (доехать) от дома до школы или спортивной секции?», затем сравните это время. Спросите ребенка: «Какая дорога заняла больше времени?». Рассматривайте примеры больших чисел с использованием расстояния. Например, задайте ребенку вопросы: «Как далеко от нас находятся самые яркие звезды?» [7, с. 159], «На каком примерно расстоянии находится тот или иной город?», «Далеко ли это?» и др.

6. Развивайте язык детей: просите их произнести вслух числа от 0 до 20, от 20 до 50, …, 100 (и обратно) и т.д. (выбирайте посильный для школьника отрезок чисел).

7. Используйте устный счет. Учите детей складывать (вычитать, умножать, делить) двузначные и трехзначные числа.

8. После окончательного усвоения таблицы умножения начните учить вместе с ребенком квадраты чисел от 1 до 10, далее от 11 до 20. Это хорошо развивает память.

9. Составляйте задания, где к числу могут быть применимы не только понятия «больше – меньше», но и «левее – правее», «ближе – дальше», «выше – ниже». Обратите внимание ребенка, что на числовой прямой числа находятся как левее, так и правее относительно какого-то числа.

10. Давайте задания на составление математических задач (даже простейших). Задавайте детям вопросы, выходящие за рамки задания: «Есть ли другой способ решения?», «Что произойдет, если изменить (добавить) следующее условие…?», «Достаточно ли данных для решения задачи?» и др.

11. Ищите разные способы решения задачи, выберите вместе с ребенком наиболее рациональный.

Делать эти упражнения необходимо систематически, по 5–10 мин, используя перерывы, в течение нескольких месяцев.

Заключение

«Чувство числа» является важной индивидуальной особенностью личности, его развитие необходимо для успешного обучения математике.

«Чувство числа» представляет собой не только способность человека определять приблизительное количество объектов без их счета, но и ряд умений, которые возникают в результате изучения математики: понимание количества, умение использовать для записи обозначающие их символы, знание понятий «больше – меньше», умение сравнивать числа и выполнять простейшие арифметические действия.

Сложность развития «чувства числа» у детей заключается в необходимости:

– научить их оперировать абстрактными понятиями;

– понятия «количество» и «порядок» интегрировать с визуальным восприятием и памятью, что затрудняется из-за путаницы цифр, сложностей с пониманием отношений «больше – меньше», восприятием многозначных чисел;

– пространственной организации правильного порядка при вычислениях и абстрактного счета (время, расстояние), а также в возможном наличии дискалькулии или других расстройств обучения, влияющих на устный счет и запоминание правил.

Учителю необходимо регулярно анализировать и учитывать развитие мышления каждого ребенка; диагностировать развитие «чувства числа» с помощью системы разноуровневых заданий; использовать различные педагогические приемы, методы, которые делают школьников активными участниками процесса обучения.