Сетевое научное издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 0,936

Введение

Научно-технический прогресс, накопление научного знания, приводит к тому, что понятия математической теории, бывшие ранее исключительно частью научных исследований, постепенно становятся полноценным компонентом образовательных систем. Это непрекращающийся процесс, характеризующий как развитие математической теории, так и развитие математического образования в целом. Он становится возможным вследствие совершенствования процесса обучения и… предполагает не столько увеличение объема передаваемой информации, сколько создание дидактических и психологических условий осмысления учения [1], когда новые элементы математической теории представлены в доступном для понимания виде на разных ступенях образования. Следуя этому процессу, в настоящее время некоторые элементы вузовского курса математики внедряются в школьные программы. В этом явлении ключевую роль играет скоординированность и корреляция содержания в соответствии с основополагающим принципом преемственности обучения, который выражается… в признании важности согласованности целей и результатов, а также содержания образования, педагогических технологий, форм и методов обучения и воспитания на смежных ступенях образования среднее общее – высшее (бакалавриат, специалитет) [2].

Рассматривая в этой концепции различные аспекты конструирования содержания вузовского обучения [3], будем исходить из более узкого понимания этого процесса, когда основные задачи по обеспечению преемственности сводятся к исключению дублирований [4], несоответствий и «разрывов» в содержании образовательных программ с целью реализации дидактических принципов научности, систематичности, последовательности [5, с. 47]. В связке школа – вуз в последнее время накапливается масса таких дублирований, так как учебный материал в школе усложняется путем добавления новых компонентов математических знаний, повторяющихся в вузе. При интенсификации школьного обучения остро стоит проблема пересмотра и коррекции вузовских курсов математики.

С другой стороны, не все декларируемое содержание школьного обучения бывает реально реализовано. Это происходит из-за объективных причин, среди них отметим следующие:

1) основное внимание учителей направлено на подготовку к ЕГЭ, а не на изучение математики как таковой [6, с. 4];

2) недостаточная подготовленность учителей к работе с материалами, пришедшими из вузовских курсов.

Необходимо понимание реального масштаба реализации освоения элементов знаний, чтобы давать рекомендации к конструированию содержания вузовского обучения в сложившихся условиях. Для этого недостаточно провести анализ нормативных документов, требуется эмпирическое исследование. Под элементами знаний в контексте настоящего исследования будем понимать математическое понятие, формулу, метод, а также их совокупность, формирующую подраздел в структуре учебных тем школьной и вузовской математики.

Цель исследования – определить наличие дублирования отдельных элементов математических знаний по факту реального освоения школьной программы для рекомендаций по коррекции содержания вузовских курсов в процессе реализации содержательной преемственности обучения.

Материал и методы исследования

Исследование проводилось в 2025 г. В нем участвовали 303 студента. Площадкой стал Кубанский государственный аграрный университет имени И.Т. Трубилина, факультеты архитектурно-строительный, электрификации, механизации. Выбор инженерных факультетов обусловлен наличием углубленного изучения математики контингента как до поступления, так и в процессе обучения.

На первом этапе определены теоретические и методологические основания исследования, разработаны процедуры сбора и оценки эмпирических данных. В результате обобщающего анализа учебных материалов, опросов и интервью выделены элементы знаний по наиболее значимым разделам математики, которые дублируются в упомянутых курсах. Была разработана анкета, состоящая из закрытых дихотомических вопросов, на основе сенситивных опросных методик [7]. Для достижения целей исследования в текст анкеты были введены уточняющие элементы графической наглядности [8], то есть рисунки с формулами, позволяющие кратко и информативно напомнить анкетируемым, о каком понятии идет речь. На втором этапе прошло анонимное анкетирование посредством заполнения бланка анкеты. На третьем этапе, при проведении качественного и количественного анализа полученных результатов применялись визуально-аналитические способы [9]. Гистограммы и таблицы составлены с помощью электронных таблиц Excel. Использованы методы описательной статистики [10; 11], чтобы выявить общее представление о данных, определить однородность групп и типичность средних. Для создания выводов и рекомендаций на основе полученных данных использованы методы систематизации и анализа информации.

Результаты исследования и их обсуждение

В результате были получены данные по структуре реального присутствия в образовательной среде школы (под этим понимаются также факультативы, школьные кружки) понятий и элементов знаний вузовского курса, глубине их освоения. Фрагмент обработанных результатов представлен на рисунке.

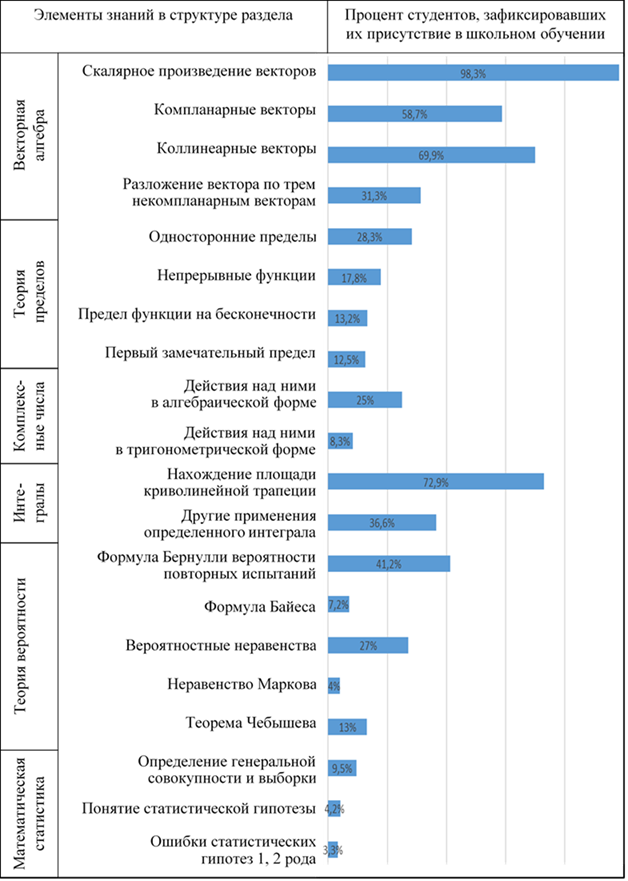
Результаты анкетирования по отдельным элементам знаний.

Примечание: составлен авторами по результатам данного исследования

Для достижения цели исследования применен особый подход в направлении повышения репрезентативности массива анкетируемых: из выборки студентов инженерных направлений исключены обучающиеся заочного факультета. Диагностика проводилась среди студентов 1–2-х курсов, у которых еще свежо представление о содержании обучения в старших классах школы и их ответы в анкете содержат минимальное число противоречий. То, что 50,5 % опрошенных в выборке изучали математику углубленно в профильных классах, позволяет считать, что они достаточно знакомы с предметом исследования.

Для контроля корректности в анкету добавили вопросы, результат ответов на которые предсказуемо высок и стабилен. Например, в вопросах по наличию в материалах обучения элементов знаний о геометрическом, физическом смысле производной и ее применению, положительные ответы ожидаемо показали высокий процент (соответственно 83,8; 91,4; 81,5 %), что подтверждает достоверность ответов как на эти вопросы, так и на всю анкету в целом.

Для оценки адекватности ответов на основные утверждения каждый раздел анкеты завершал обобщающий вопрос, который содержал альтернативное упомянутым высказывание. На такой вопрос, содержащий предположение о не присутствии в целом той или иной темы в учебном процессе школы, получены положительные ответы: «Производные» – 1,6 %, «Первообразные и интегралы» – 23,1 %, «Векторная алгебра» – 2,64 %, «Теория пределов» – 65 %, «Комплексные числа» – 67,9 %. В теории вероятностей положительный ответ на этот вопрос получен по отдельным элементам знаний: «Формула Байеса» – 92,7 %, «Формула Бернулли» – 58,7 %; по обоснованиям закона больших чисел – 85,5 %. Отметим, что отрицательный ответ студента на присутствие в курсе определенных элементов знаний не означает их полного отсутствия в материалах школьного обучения. В этом случае можно сделать вывод, что он изучался фрагментарно или в слишком быстром темпе. Уделялось так мало внимания, что обучающиеся не зафиксировали его наличие. Например, 87,7 % считают, что в их обучении не было темы «Математическая статистика», присутствующей в рабочих программах.

В ходе обработки результатов анкетирования приобрел актуальность вопрос об однородности данных и типичности средних. Решение его осуществлялось путем расчета коэффициента вариации исходя из результатов по отдельным академическим группам. Коэффициент вариации не более 30 % определяет выборочную совокупность как однородную, а средние величины, полученные по ней, – более типичными. При этом не всегда выполнялась прямая зависимость: чем больше анкетируемых считают эту тему знакомой со школы, тем ниже показатель коэффициента вариации, однороднее выборочная совокупность. Зафиксированы однородные результаты ответов по пунктам: векторная алгебра, производные, первообразные и интегралы, формула Бернулли вероятности повторных испытаний и формула Байеса. Средний процент студентов, считающих, что эти темы изучали ранее, будем считать более типичным. А полученные результаты – более точными и надежными. Неоднородность ответов обучаемых по некоторым пунктам анкеты позволяет сделать вывод о разнохарактерном уровне подготовки обучаемых в пределах изучения отдельных математических понятий. В таком случае при отборе содержания высшего образования не следует ориентироваться на процент ознакомившихся с этой темой. Необходимо изучать тему основательно и последовательно, начиная с базовых понятий.

Также в процессе обобщения результатов отмечена зависимость между присутствием элемента знаний в контрольно-измерительных материалах единого государственного экзамена по образовательным программам среднего общего образования и широкому охвату обучающихся, которые зафиксировали его в своей памяти как изученный. К таким относятся элементы векторной алгебры, производные, основные элементы теории вероятностей. Это подтверждает предположение о том, что в старших классах особое внимание уделяется подготовке к ЕГЭ, иногда за счет других тем.

Учитывая, что все темы учебного курса должны изучаться целостно, последовательно, начиная с основных понятий, по результатам исследования предлагаются следующие рекомендации.

1. С основными понятиями векторной алгебры обучающиеся знакомы со школы. Это позволит в вузовском курсе не тратить на них много времени и основной акцент направить на более усложненные математические конструкции на базе этих понятий.

2. Реальное изучение комплексных чисел и связанных с ними элементов теории в школе даже на базе факультативов встречается крайне редко. Эти крайне абстрактные понятия следует изучать с самых основ.

3. В настоящее время все чаще наблюдается присутствие некоторых элементов теории пределов в школе. Опросы показывают, что обучающиеся слабо различают понятия непосредственно предела, одностороннего предела, первого замечательного предела. Указанная тема сложна для восприятия, что детерминирует ее основательное изучение на базе высшей школы. Эти и связанные с ними понятия следует изучать «с нуля».

4. Подавляющее большинство студентов считает понятия неопределенного и определенного интеграла известными со школы. Следует больше времени уделить геометрическим и физическим приложениям интегралов посредством использования профильных задач [12].

5. К основным понятиям и теоремам теории вероятностей обучающиеся обращались, особенно в процессе подготовки к ОГЭ и ЕГЭ. Чуть меньше половины знают о формуле Бернулли для вероятности повторных испытаний. Но декларируемые в материалах для обучения вероятностные неравенства, неравенства Маркова, теорема Чебышева, а также более усложненные схемы вычисления вероятностей (например, формулы Байеса) не были изучены. В вузе начальные понятия теории вероятности можно изучить достаточно бегло, уделив внимание более глубоким понятиям, таким как математические обоснования закона больших чисел.

6. Отдельные понятия математической статистики студентам знакомы со школы (мода, медиана). Но в их сознании не сложились представления об этом разделе математики как о целостной структуре, в основе которой лежат понятия генеральной и выборочной совокупности. Теорию проверки статистических гипотез подавляющее большинство считает для себя неизвестной. Это необходимо учитывать при построении обучения.

7. Понятие производной, ее вычисление, приложения и нахождение экстремальных значений обучающимися освоены на достаточно высоком уровне. В связи с этим в вузовском обучении появляется возможность изучить их глубже, уделяя большее внимание решению профессионально ориентированных задач на эти элементы теории.

Есть основания полагать, что со временем в высшую школу будет поступать все больше студентов с начальными знаниями, повторяющими часть содержания вузовского обучения. При этом нецелесообразно создателям вузовских курсов каждый год отслеживать глубину освоения школьных программ. «Динамика предметных результатов обучения математике представляет собой сложный и многоуровневый процесс, который включает в себя как количественный, так и качественный мониторинг изменений в освоении математических концепций» [13]. Вследствие изменчивости этого состояния ежегодная диагностика для информирования создателей курсов – трудоемкая процедура.

В связи с этим требуются новые подходы к отбору содержания курса математики в вузе, предполагающие возможности варьирования, но в то же время сохраняющие фундаментальное теоретическое ядро и высокий теоретический уровень изучения [14]. Моделью для построения курса математики должна стать гибкая и мобильная конструкция, отвечающая изменчивому состоянию современного образования. Она должна отвечать требованиям персонализированной подготовки специалистов цифровой экономики [15], предполагающей в себе как вариативность содержания, так и методов изучения математики, позволяющие перейти на другой уровень сложности изложения фундаментальных положений теории. В эту модель необходимо органично вписать возможность математического моделирования процессов будущей профессиональной деятельности или явления окружающего мира. Это позволит наполнить в вузовском курсе новыми смыслами изученные в школе элементы знаний, создаст необходимое усложнение и расширение учебного материала за счет решения профессионально ориентированных задач.

Заключение

Полученные данные имеют практическую значимость, методы сбора и обработки позволяют их оценивать как достаточно полные и достоверные. Результаты анкетирования показывают, что следует осторожно подходить к изменениям в содержании вузовского обучения, даже если считается, что некоторые его элементы изучены в школе. В этих условиях необходимо сохранить высокий теоретический уровень и, как следствие, авторитет высшего образования. Важно использовать новые концепции и принципы в конструировании вузовского курса математики. В поиске моделей реализации приведенных указаний для построения содержания обучения и будет продолжено настоящее исследование.