Введение
Согласно Федеральному государственному образовательному стандарту высшего образования (ФГОС ВО), современное обучение в области математических дисциплин направлено на формирование у студентов аналитического, алгоритмического и вероятностного мышления, а также навыков работы с данными и моделирования сложных процессов. В этом контексте численные методы, в частности метод Монте-Карло, становятся хорошим инструментом для изучения процессов с элементами случайности и неопределенности, обеспечивая практическую основу для формирования компетенций в математическом моделировании [1].
В математике метод Монте-Карло применяется, например, для приближенного вычисления интегралов высокой размерности и исследования случайных процессов [2]. В физике, химии и инженерии он используется для моделирования сложных процессов, таких как теплоперенос, механика жидкостей, динамика частиц, а также для расчета вероятностей отказов систем и оптимизации конструкций на основе численных экспериментов [3, 4]. В экономике и финансах метод позволяет моделировать риски, прогнозировать вероятностные сценарии и оценивать последствия неопределенности [5]. В биологии и медицине его применяют, например, для исследования процессов распространения заболеваний и оценки эффективности лекарственных препаратов с использованием виртуальных экспериментов [6].
Метод Монте-Карло также находит активное применение в образовательном процессе. Он используется для формирования у студентов навыков математического моделирования, анализа и интерпретации данных, а также для развития аналитического, алгоритмического и вероятностного мышления [7]. Виртуальные эксперименты и численные модели позволяют обучающимся на практике осваивать сложные стохастические процессы, визуализировать распределения данных и проверять гипотезы в безопасной и наглядной форме.
Таким образом, универсальность метода и его широкая область применения делают его ценным инструментом как для научных исследований, так и для образовательных целей, что обосновывает необходимость его изучения и внедрения в учебный процесс математических дисциплин в вузе.
Цель исследования – выявление дидактических функций метода Монте-Карло, способствующих формированию аналитического, алгоритмического, вероятностного мышления и исследовательских компетенций студентов.
Для достижения поставленной цели автором выделены следующие задачи:
1) проанализировать алгоритм метода Монте-Карло и основные этапы его реализации в образовательном процессе;
2) определить дидактические функции метода Монте-Карло, способствующие формированию у студентов аналитического мышления, исследовательских компетенций и навыков визуализации и интерпретации данных.
Материал и методы исследования
Материалами исследования являются научные публикации в области методики преподавания математики, педагогики, информатики и прикладного моделирования. Методы исследования включают анализ отечественных и зарубежных источников для выявления принципов применения метода Монте-Карло в образовательной практике. Кроме того, использован педагогический опыт автора в преподавании математических дисциплин в вузе, включающий проведение практических и лабораторных занятий с применением численных моделей, виртуальных экспериментов и компьютерных инструментов для формирования исследовательских и вычислительных навыков студентов.
Применение выбранных материалов и методов позволило получить результаты исследования, выявляющие особенности использования метода Монте-Карло в образовательном процессе.
Результаты исследования и их обсуждение
Метод Монте-Карло – это стохастический численный метод, основанный на моделировании случайных процессов и использовании случайных величин для решения задач, где прямое аналитическое решение затруднительно или невозможно.
История метода Монте-Карло развивалась постепенно. Идея использования случайных экспериментов для оценки численных величин известна с XVIII–XIX вв.: классический пример – «игла Бюффона», когда многократное бросание иглы на пронумерованную поверхность позволяет оценить число π. К концу 1940-х гг., в работах Станислава Улама и Джона фон Неймана, метод получил современную формулировку и был представлен как систематизированный подход к численному моделированию сложных процессов С. Улам пришел к идее во время реабилитации после болезни, заметив, что можно многократно моделировать случайные события вместо полного аналитического решения задачи. Позже вместе с фон Нейманом он применял метод для решения вычислительных задач в рамках проекта Манхэттен – масштабной исследовательской программы США по разработке новых технологий. Название «Монте-Карло» предложил их коллега Николас Метрополис в честь знаменитого казино, подчеркивая случайный характер метода.
Таким образом, современный метод Монте-Карло сочетает историческую традицию случайных экспериментов с научной разработкой середины XX в. и получил широкое признание как надежный инструмент в различных науках.
Суть метода – проведение большого числа случайных экспериментов для оценки величин, с последовательными этапами: моделирование, обработка, визуализация и получение приближенного решения. Для практической реализации этих принципов используется пошаговый алгоритм метода Монте-Карло, который систематизирует процесс моделирования и обеспечивает последовательность и структурированность выполнения экспериментов.
Алгоритм метода Монте-Карло
1. Формулировка задачи. На этом этапе четко определяется цель моделирования и выбираются показатели, которые необходимо оценить.
2. Построение вероятностной модели. Создается математическая модель, описывающая случайные события или величины, участвующие в процессе.
3. Генерация случайных чисел и проведение экспериментов. С помощью генераторов случайных чисел моделируются многочисленные эксперименты в соответствии с заданной вероятностной моделью. Каждый эксперимент представляет собой реализацию случайного события или процесса, что позволяет получить статистически значимые результаты.
4. Обработка, анализ и визуализация результатов. На этом этапе проводится обработка данных, полученных в ходе экспериментов. Вычисляются статистические характеристики, которые позволяют оценить искомую величину и получить приближенное решение задачи. Для наглядного представления результатов применяются инструменты визуализации. Кроме того, полученные экспериментальные данные часто сравниваются с известными теоретическими результатами или аналитическими решениями, что позволяет оценить точность метода и выявить возможные отклонения. В образовательном контексте это особенно важно, так как помогает студентам понять, насколько результаты моделирования соответствуют ожидаемым значениям и оценить надежность метода.
5. Проверка точности и корректировка модели. Заключительный этап включает оценку точности и устойчивости полученного результата. При необходимости корректируются параметры модели, проводится повторное моделирование для повышения достоверности и надежности оценки.
Знакомство студентов с методом Монте-Карло целесообразно начинать с простых и популярных примеров, для которых известны точные аналитические решения. Это позволяет наглядно продемонстрировать степень точности метода, понять принципы генерации случайных чисел и моделирования, а также сравнить результаты численного эксперимента с теоретическим значением. Такие задачи создают основу для формирования навыков математического моделирования, анализа данных и интерпретации результатов, после чего обучающиеся могут переходить к более сложным и прикладным задачам в рамках курсов по высшей математике и теории вероятностей [8].
В качестве одного из таких примеров может быть использовано задание, позволяющее продемонстрировать применение метода Монте-Карло на модели с известным аналитическим решением.
Задание № 1. Баланс ресурсов предприятия
Предприятие производит три вида продукции: A, B и C. Каждый вид продукции требует определенного количества труда, сырья и оборудования. Определите объемы выпуска продукции при ограниченных ресурсах и проверьте, можно ли полностью использовать имеющиеся запасы. Смоделируйте задачу методом Монте-Карло в Python или Excel. Сгенерируйте множество случайных распределений ресурсов (труда, сырья, оборудования), которые приблизительно удовлетворяют ограничениям запасов. Для каждого варианта вычислите значение целевой функции. Проанализируйте распределение полученных результатов: выявите комбинации ресурсов, обеспечивающие максимальную прибыль, а также сценарии, где использование ресурсов ограничено или неэффективно.
Для трех видов продукции известны нормы расхода ресурсов и их запасы, прибыль за единицу. В табл. 1 представлены условия задания.
Таблица 1
Условия задания «Баланс ресурсов предприятия»
|
Продукция |
Труд |
Сырье |
Оборудование (часы) |
Прибыль за единицу |
|
A |
2 |
3 |
1 |
50 |
|
B |
4 |
2 |
2 |
70 |
|
C |
3 |
5 |
4 |
90 |
|
Запасы |
100 |
120 |
60 |
Примечание: составлена автором на основе полученных данных в ходе исследования
Фрагмент решения. Требуется максимизировать прибыль Z = 50xA + 70xB + 90xC →max, при линейных ограничениях ресурсов: 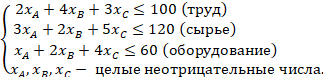
Аналитическое решение линейной модели дает оптимальный производственный план XA = 28, XB = 8, XC = 4, с полной загрузкой имеющихся запасов по всем трем ресурсам и максимальной прибылью Zmax = 2320.
Для решения методом Монте-Карло может быть использовано табличное моделирование в Excel. Такой подход позволяет формализовать исходные данные, выполнить вычисления в удобной структурированной форме и наглядно проверить, достигается ли полное использование доступных ресурсов. Решение задачи методом линейного программирования представлено в табл. 2.
Таблица 2
Решение задания «Баланс предприятия» с помощью линейного программирования в Excel
|
№ |
A |
B |
C |
D |
E |
F |
G |
H |
|
1 |
Продукция |
Труд |
Сырье |
Оборудование (часы) |
Прибыль за единицу |
Верхняя граница |
X |
Прибыль |
|
2 |
A |
2 |
3 |
1 |
50 |
40 |
28 |
1400 |
|
3 |
B |
4 |
2 |
2 |
70 |
25 |
8 |
560 |
|
4 |
C |
3 |
5 |
4 |
90 |
15 |
4 |
360 |
|
5 |
Запасы |
100 |
120 |
60 |
2320 |
|||
|
6 |
Ограничения |
100 |
120 |
60 |
|
|
|
Примечание: составлена автором на основе полученных данных в ходе исследования
В решении использован инструмент «Поиск решения» и следующие формулы:
Ограничения для труда = B2*$G2+B3*$G3+B4*$G4 (труд);
Верхняя граница для А = МИН(B$5/B2; C$5/C2; D$5/D2);
Прибыль для А = E2*G2; Целевая функция = СУММ(H2:H4)
Популярное задание «Баланс ресурсов предприятия» может быть представлено и в формате стохастического моделирования. Применение метода Монте-Карло позволяет варьировать параметры расхода ресурсов и прибыли в допустимых диапазонах, оценивая устойчивость решения и возможные отклонения от оптимального плана. Таблица 3 демонстрирует пример такого моделирования.
Таблица 3
Фрагмент решения задания «Баланс предприятия» с помощью метода Монте-Карло в Excel
|
№ |
A |
B |
C |
D |
E |
F |
G |
H |
I |
|
8 |
A |
B |
C |
Труд |
Сырье |
Оборудование |
Выполнение ограничений |
Прибыль |
Максимальная прибыль |
|
9 |
37 |
3 |
9 |
113 |
162 |
79 |
0 |
0 |
2320 |
|
10 |
18 |
12 |
2 |
90 |
88 |
50 |
1 |
1920 |
|
|
11 |
14 |
25 |
9 |
155 |
137 |
100 |
0 |
0 |
|
|
12 |
7 |
11 |
4 |
70 |
63 |
45 |
1 |
1480 |
|
|
13 |
37 |
16 |
8 |
162 |
183 |
101 |
0 |
0 |
|
|
… |
|
|
|
|
|
|
|
|
|
|
33708 |
28 |
8 |
4 |
100 |
120 |
60 |
1 |
2320 |
|
|
… |
|
|
|
|
|
|
|
|
|
|
100008 |
26 |
23 |
0 |
144 |
124 |
72 |
0 |
0 |
|
Примечание: составлена автором на основе полученных данных в ходе исследования
В решении использована генерация случайных чисел и следующие формулы:
A = СЛУЧМЕЖДУ(0;F$2); B = СЛУЧМЕЖДУ(0;F$3); C = СЛУЧМЕЖДУ(0;F$4);
Труд = B$2*$A9 + B$3*$B9 +B$4*$C9;
Сырье = C$2*$A9 + C$3*$B9 +C$4*$C9;
Оборудование = D$2*$A9 + D$3*$B9 +D$4*$C9;
Выполнение ограничений = ЕСЛИ(И(D9< = B$5;E9< = C$5;F9< = D$5);1;0);
Прибыль = ЕСЛИ(G9 = 1;E$2*A9+E$3*B9+E$4*C9;0);
Максимальная прибыль = МАКС(H$9:H$100008).
Для быстрого копирования нескольких формул на большой диапазон строк в электронных таблицах применяется следующий подход: выделяются ячейки с формулами (например, A9:H9), после чего в поле имени ячейки указывается диапазон, на который требуется распространить формулы, например, A9:H100008, затем ввод подтверждается нажатием клавиши Enter. После выделения всего диапазона используется сочетание клавиш Ctrl+D, что обеспечивает одновременное распространение всех восьми формул на 100 000 строк с сохранением относительных ссылок в формулах.
Подобные задачи также можно решать с использованием языка программирования Python [9, 10]. В листинге 1 представлен фрагмент реализации метода Монте-Карло для задачи оптимального распределения ресурсов предприятия.
Листинг 1
Фрагмент решения задания «Баланс предприятия» методом Монте-Карло на Python
import numpy as np
import pandas as pd
# ПАРАМЕТРЫ ЗАДАЧИ
# Прибыль за единицу продукции A, B, C
c = np.array([50, 70, 90], dtype = float)
# Нормы расхода ресурсов (труд, сырье, оборудование)
A = np.array([
[2, 4, 3], # труд
[3, 2, 5], # сырье
[1, 2, 4] # оборудование
], dtype = float)
# Запасы ресурсов
b = np.array([100, 120, 60], dtype = float)
# ВЕРХНИЕ ГРАНИЦЫ ДЛЯ ПЕРЕМЕННЫХ
# Максимально возможные объемы продукции, исходя из каждого ресурса
upper_bounds = np.array([
int(min([b[j] / A[j, i] for j in range(3) if A[j, i] > 0]))
for i in range(3)
])
print("Верхние границы для продукции A, B, C:", upper_bounds)
# МЕТОД МОНТЕ-КАРЛО
def monte_carlo_integer(samples = 100000, seed = None):
rng = np.random.default_rng(seed)
# Генерация случайных целых точек в диапазоне [0, upper_bounds]
X = np.zeros((samples, 3), dtype = int)
for i in range(3):
X[:, i] = rng.integers(0, upper_bounds[i]+1, size = samples)
# Проверка ограничений A x < = b
feasible_mask = np.all(A @ X.T < = b.reshape(-1,1), axis = 0)
feasible_points = X[feasible_mask]
# Вычисление прибыли для допустимых комбинаций
profits = feasible_points @ c
return feasible_points, profits, feasible_mask
# Запуск моделирования
feasible_points, profits, feasible_mask = monte_carlo_integer(samples = 100000)
prob_feasible = len(feasible_points) / 100000
print(f"\nДопустимых комбинаций: {len(feasible_points)} из 100000")
print(f"Вероятность допустимых значений: {prob_feasible:.2%}")
# ЛУЧШЕЕ РЕШЕНИЕ
best_index = np.argmax(profits)
best_point = feasible_points[best_index]
best_profit = profits[best_index]
best_A, best_B, best_C = best_point
# ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ
mean_profit = np.mean(profits) # средняя прибыль
median_profit = np.median(profits) # медиана прибыли
var_profit = np.var(profits, ddof = 1) # выборочная дисперсия
std_profit = np.std(profits, ddof = 1) # стандартное отклонение
# Массив прибылей, куда недопустимые решения записываются как 0
profits_with_zeros = np.zeros(100000)
profits_with_zeros[feasible_mask] = profits
var_profit0 = np.var(profits_with_zeros, ddof = 1) # дисперсия с учетом нулевых прибылей
std_profit0 = np.std(profits_with_zeros, ddof = 1) # стандартное отклонение с учетом нулевых прибылей
threshold = 2000
prob_over_threshold = np.mean(profits > threshold)
# ТОП-10 ЛУЧШИХ РЕШЕНИЙ
df = pd.DataFrame(feasible_points, columns = ["A", "B", "C"])
df["profit"] = profits
df_top10 = df.sort_values("profit", ascending = False).head(10)
# ВЫВОД РЕЗУЛЬТАТОВ
print("\nМаксимальная прибыль и соответствующие объемы продукции:")
print(f"Прибыль = {best_profit} при A = {best_A}, B = {best_B}, C = {best_C}")
print("\nЧисловые характеристики прибыли:")
print(f"Среднее: {mean_profit:.2f}")
print(f"Медиана: {median_profit}")
print(f"Дисперсия: {var_profit:.2f}")
print(f"Стандартное отклонение: {std_profit:.2f}")
print(f"Дисперсия с учетом нулевых прибылей: {var_profit0:.2f}")
print(f"Стандартное отклонение с учетом нулевых прибылей: {std_profit0:.2f}")
print(f"Вероятность прибыли(без учета прибылей = 0) > {threshold}: {prob_over_threshold:.2%}")
print(f"Количество уникальных комбинаций: {len(np.unique(feasible_points, axis = 0))}")
print("\nТоп-10 лучших найденных решений:")
print(df_top10)
Код реализует метод Монте-Карло для распределения ресурсов предприятия. Генерируются случайные комбинации объемов продукции, проверяется их допустимость по ограничениям ресурсов, вычисляется прибыль для каждой допустимой комбинации. Рассчитываются числовые характеристики прибыли: среднее, медиана, дисперсия, стандартное отклонение, вероятность превышения порога, а также определяется максимальная прибыль и соответствующая комбинация выпуска продукции. Результаты наглядно демонстрируют распределение возможных решений.
Для решения задания студентам необходимо опираться на знания из различных областей – экономики, линейного программирования и информатики. Метод Монте-Карло в данном случае применяется не для точного решения задачи, а как инструмент моделирования. Он позволяет студентам: наглядно изучить влияние изменения запасов ресурсов на оптимальное решение; оценить устойчивость результатов к вариациям входных данных; развивать навыки экономического моделирования и практического применения математических методов. Педагогический эффект проявляется в формировании у студентов способности применять абстрактные знания к реальным экономическим ситуациям и видеть взаимосвязи между разными дисциплинами.
После того как метод Монте-Карло был продемонстрирован на задаче, которая может быть решена стандартными методами, со студентами на занятиях по высшей математике можно рассмотреть более абстрактные задачи, например вычисление многомерных интегралов.
Далее автором будет рассмотрен пример вычисления 50-мерного интеграла функции 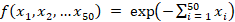 с использованием метода Монте-Карло.
с использованием метода Монте-Карло.
Задание № 2. Интегралы на многомерных кубах и метод Монте-Карло
Одномерный гиперкуб [0,1]1 представляет собой отрезок на числовой прямой от 0 до 1. В рамках интегрирования это соответствует учету всех точек на данном отрезке.
Одномерный интеграл – площадь под кривой 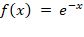 .
.
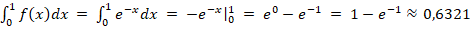 .
.
Двумерный гиперкуб [0,1]2 задается как декартово произведение отрезков: [0,1]2 = [0,1]×[0,1]. Геометрически это квадрат, где координаты 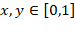 .
.
Двумерный интеграл – объем под поверхностью 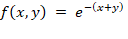 на квадрате [0,1]².
на квадрате [0,1]².
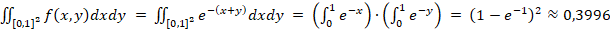 .
.
Трехмерный гиперкуб задается аналогично: [0,1]3 = [0,1]×[0,1]×[0,1], где координаты 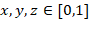 . Интеграл по кубу рассматривается как сумма (интегрирование) значений функции во всем объеме куба. При интегрировании учитывается вклад функции f (x, y, z) в каждой точке куба, складывая его для всех точек непрерывно. Трехмерный интеграл – объем под функцией
. Интеграл по кубу рассматривается как сумма (интегрирование) значений функции во всем объеме куба. При интегрировании учитывается вклад функции f (x, y, z) в каждой точке куба, складывая его для всех точек непрерывно. Трехмерный интеграл – объем под функцией 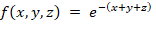 на кубе [0,1]³.
на кубе [0,1]³.
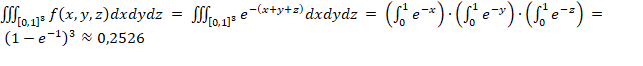 .
.
50-мерный гиперкуб [0,1]50 – это множество точек 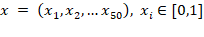 . Каждая точка характеризуется 50 координатами, каждая из которых лежит в интервале [0,1]. Интеграл по 50-мерному кубу записывается как
. Каждая точка характеризуется 50 координатами, каждая из которых лежит в интервале [0,1]. Интеграл по 50-мерному кубу записывается как 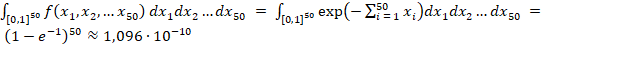 . Здесь аналитическое решение возможно из-за разложения функции на множители.
. Здесь аналитическое решение возможно из-за разложения функции на множители.
Метод Монте-Карло во всех этих примерах также применим: для численной аппроксимации выбирается N случайных точек 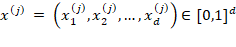 , вычисляются значения функции
, вычисляются значения функции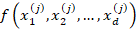 , затем усредняются значения:
, затем усредняются значения: 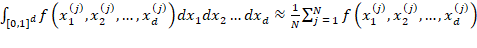 .
.
Представленный фрагмент кода на Python (листинг 2) реализует численное вычисление многомерных интегралов вида 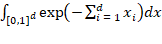 с использованием метода Монте-Карло.
с использованием метода Монте-Карло.
Листинг 2
Вычисление интеграла функции 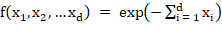
import numpy as np
N = 1_000_000
# 1D интеграл
x1 = np.random.uniform(0, 1, N)
f1 = np.exp(-x1)
I1_mc = np.mean(f1)
std1 = np.std(f1, ddof = 1) / np.sqrt(N)
print(f"1D интеграл: {I1_mc:.6f} ± {std1:.6f}")
# 2D интеграл
x2 = np.random.uniform(0, 1, N)
y2 = np.random.uniform(0, 1, N)
f2 = np.exp(-(x2 + y2))
I2_mc = np.mean(f2)
std2 = np.std(f2, ddof = 1) / np.sqrt(N)
print(f"2D интеграл: {I2_mc:.6f} ± {std2:.6f}")
# 3D интеграл
x3 = np.random.uniform(0, 1, N)
y3 = np.random.uniform(0, 1, N)
z3 = np.random.uniform(0, 1, N)
f3 = np.exp(-(x3 + y3 + z3))
I3_mc = np.mean(f3)
std3 = np.std(f3, ddof = 1) / np.sqrt(N)
print(f"3D интеграл: {I3_mc:.6f} ± {std3:.6f}")
# 50D интеграл
d50 = 50
x50 = np.random.uniform(0, 1, (N, d50))
f50 = np.exp(-np.sum(x50, axis = 1))
I50_mc = np.mean(f50)
std50 = np.std(f50, ddof = 1) / np.sqrt(N)
print(f"50D интеграл: {I50_mc:.6e} ± {std50:.6e}")
Код демонстрирует ключевое преимущество метода Монте-Карло: слабую зависимость точности от размерности пространства, что делает его особенно актуальным при интегрировании функций в высоких измерениях. Для размерностей d = 1, 2, 3 и d = 50 генерируется одинаковое количество равномерно распределенных случайных точек в гиперкубе [0,1]d. Далее вычисляются значения подынтегральной функции, после чего среднее значение по выборке используется как несмещенная оценка интеграла. Стандартная ошибка вычисляется как 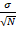 , где σ – выборочное стандартное отклонение значений функции.
, где σ – выборочное стандартное отклонение значений функции.
Замена суммирования на произведение в функции 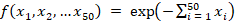 существенно усложняет структуру интегрируемой функции, делая задачу более сложной и тем самым значительно повышая методологический интерес примера с точки зрения применения метода Монте-Карло.
существенно усложняет структуру интегрируемой функции, делая задачу более сложной и тем самым значительно повышая методологический интерес примера с точки зрения применения метода Монте-Карло.
Далее рассматривается вычисление интеграла 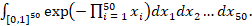
В отличие от функции вида 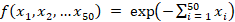 данный интеграл не может быть разложен на произведение одномерных компонент. Это делает применение метода Монте-Карло особенно рациональным для численной оценки интеграла. Представленный фрагмент кода на Python (листинг 3) реализует численное вычисление 50-мерного интеграла экспоненциального вида
данный интеграл не может быть разложен на произведение одномерных компонент. Это делает применение метода Монте-Карло особенно рациональным для численной оценки интеграла. Представленный фрагмент кода на Python (листинг 3) реализует численное вычисление 50-мерного интеграла экспоненциального вида 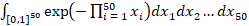 .
.
Листинг 3
Вычисление интеграла функции 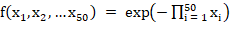
import random
from decimal import Decimal, getcontext
import math
# Настройки
getcontext().prec = 50 # точность Decimal
N_decimal = 100_000 # число случайных точек (уменьшено для скорости)
d50 = 50 # размерность интеграла
# Метод Монте-Карло (Decimal)
f_values = [] # сохраняются значения функции для std
for i in range(N_decimal):
point = [Decimal(random.random()) for _ in range(d50)]
prod = Decimal(1)
for x in point:
prod * = x
f_val = Decimal.exp(-prod)
f_values.append(f_val)
if (i+1) % 10000 = = 0:
print(f"Обработано {i+1} точек")
# Среднее значение интеграла
I_mc_decimal = sum(f_values) / N_decimal
# Стандартная ошибка (несмещенная оценка)
mean = I_mc_decimal
variance = sum((x - mean)**2 for x in f_values) / (N_decimal - 1) # деление на N-1
std_error = variance.sqrt() / Decimal(N_decimal).sqrt()
print(f"\n50D интеграл (Monte Carlo Decimal) : {I_mc_decimal}")
print(f"Стандартная ошибка : {std_error}")
# Метод Тейлора (Decimal)
I_series = Decimal(0)
k = 0
max_terms = 200
while k < max_terms:
term = Decimal((-1)**k) / Decimal(math.factorial(k)) / Decimal(k+1)**d50
I_series + = term
if abs(term) < Decimal('1e-50'):
break
k + = 1
print(f"50D интеграл (ряд Тейлора) : {I_series}")
# Абсолютная погрешность
abs_error = abs(I_mc_decimal - I_series)
print(f"Абсолютная погрешность : {abs_error}")
Данный код реализует численное вычисление 50-мерного интеграла функции 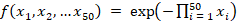 двумя способами. Первый способ использует метод Монте-Карло с высокой точностью (Decimal), оценивая интеграл через среднее значение функции на случайной выборке из 100 000 точек и вычисляя стандартную ошибку оценки. Второй способ применяет разложение функции в ряд Тейлора с последующей суммой аналитических членов, что обеспечивает высокую точность результата. В конце вычисляется абсолютная погрешность между оценкой методом Монте-Карло и результатом ряда Тейлора, что позволяет количественно оценить точность численной аппроксимации. Применение метода Монте-Карло здесь также служит независимым источником проверки и контроля точности, подтверждая результаты, полученные другим численным способом. Абсолютная погрешность между оценкой методом Монте-Карло и результатом ряда Тейлора оказывается крайне малой (при 100 000 случайных точек примерно 5⋅10−16), что подтверждает корректность реализации обоих методов.
двумя способами. Первый способ использует метод Монте-Карло с высокой точностью (Decimal), оценивая интеграл через среднее значение функции на случайной выборке из 100 000 точек и вычисляя стандартную ошибку оценки. Второй способ применяет разложение функции в ряд Тейлора с последующей суммой аналитических членов, что обеспечивает высокую точность результата. В конце вычисляется абсолютная погрешность между оценкой методом Монте-Карло и результатом ряда Тейлора, что позволяет количественно оценить точность численной аппроксимации. Применение метода Монте-Карло здесь также служит независимым источником проверки и контроля точности, подтверждая результаты, полученные другим численным способом. Абсолютная погрешность между оценкой методом Монте-Карло и результатом ряда Тейлора оказывается крайне малой (при 100 000 случайных точек примерно 5⋅10−16), что подтверждает корректность реализации обоих методов.
Рассмотренные примеры демонстрируют эффективность метода Монте-Карло для численного решения задач и выявляют образовательный потенциал метода Монте-Карло, делая абстрактные понятия наглядными и экспериментально проверяемыми.
На основе анализа литературы и педагогического опыта автором выделены ключевые дидактические функции метода Монте-Карло, оказывающие существенное влияние на образовательный процесс при изучении математических дисциплин в вузе и формировании цифровых компетенций студентов.
Интеграция математических дисциплин с цифровыми инструментами.
Метод Монте-Карло позволяет выстраивать учебные задания в единой рамке «моделирование → вычисление → визуализация → интерпретация», сочетая математику с элементами программирования и обработки данных. Обучающиеся используют цифровые инструменты для анализа и обработки информации, что дает возможность наглядно исследовать математические модели, прослеживать влияние вариативности и выявлять закономерности. При этом проявляется связь математики с информатикой, экономикой, инженерией и другими областями, демонстрируя практическое применение численных методов в решении разнообразных задач [11]. Интеграция метода в учебный процесс формирует междисциплинарное мышление (способность видеть и использовать связи между различными областями знаний) и подготавливает обучающихся к последующим этапам моделирования и экспериментальной работы [12].
Формирование навыков математического моделирования. Метод Монте-Карло начинается с построения вероятностной модели, отражающей структуру задачи, заданные ограничения и случайные факторы. Построение модели включает выбор параметров, формулировку стохастической схемы, определение случайных величин и правил их генерации, что формирует понимание перехода от реальной ситуации к ее математической формализации. Моделирование создает основу для последующих этапов – визуализации, интерпретации и анализа данных. Этот процесс развивает математическое мышление (способность структурировать задачи, выявлять закономерности и строить логически обоснованные выводы), подготавливая обучающихся к системной работе с математическими и стохастическими моделями [13].
Проведение виртуальных экспериментов для дорогостоящих и трудновоспроизводимых процессов. Виртуальные эксперименты с использованием метода Монте-Карло предоставляют возможность исследовать процессы, которые трудно или невозможно воспроизвести в реальности, экономя ресурсы, время и средства. Обучающиеся планируют и проводят такие эксперименты, варьируют параметры моделей, анализируют результаты и формулируют обоснованные выводы, не подвергая риску реальные объекты или системы. Деятельность развивает экспериментальную самостоятельность, аналитические навыки и способность системно оценивать последствия изменений в моделях [14].
Упрощение освоения сложных математических идей через эксперимент. При работе с трудными для аналитического решения задачами, такими как многомерные распределения, интегралы высокой размерности или модели с неопределенными параметрами, обучающиеся переходят к экспериментальному исследованию. Они планируют и проводят численные эксперименты, варьируют параметры модели, наблюдают динамику изменений и систематизируют результаты. Такой подход позволяет глубже понять структуру и поведение сложных процессов, выявлять закономерности и проверять гипотезы на практике. В процессе работы формируются навыки экспериментальной самостоятельности, внимательности к данным и критической оценки результатов [15].
Освоение последовательного и логического подхода к решению задач. Работа с методом Монте-Карло выстраивает у обучающихся системный процесс решения задач, основанный на последовательном разбиении задачи на этапы и логической организации действий. Такой формат деятельности развивает алгоритмическое мышление – способность планировать шаги, выявлять закономерности и оформлять структурированное решение. Обучающиеся учатся формулировать стратегию, упорядочивать информацию и делать обоснованные выводы. Последовательная организация работы способствует формированию устойчивых подходов к решению как конкретных, так и абстрактных задач и создает фундамент для последующего анализа данных и интерпретации результатов экспериментов.
Развитие вычислительных навыков при работе с многомерными данными. Метод Монте-Карло развивает у обучающихся вычислительные способности, необходимые для реализации моделей, генерации случайных данных и проведения численных экспериментов. Обучающиеся осваивают методы обработки и анализа данных, учитывают погрешности и вариативность, сравнивают альтернативные подходы и проверяют достоверность полученных результатов. Постоянная практика в решении задач с многомерными и неопределенными данными укрепляет уверенность в использовании вычислительных инструментов и формирует навыки системной работы с данными, что является основой для дальнейшего развития аналитического мышления – способности выделять существенные элементы, выявлять закономерности и делать обоснованные выводы на основе анализа информации.
Формирование навыков визуализации и интерпретации результатов. Метод Монте-Карло дает обучающимся возможность наглядно представлять стохастические процессы и результаты численных экспериментов, что помогает понять распределение данных, разброс результатов и влияние случайных факторов. Обучающиеся учатся визуализировать данные различных моделей, сравнивать их между собой и выявлять закономерности в процессах. Такая практика формирует интерпретационные навыки – способность системно анализировать данные и делать обоснованные выводы, оценивая достоверность результатов и принимая решения на основе анализа информации.
Сравнение аналитических и численных методов. Метод Монте-Карло помогает обучающимся понимать различия между строгими аналитическими решениями и численными экспериментами, выявлять сильные и слабые стороны каждого подхода и оценивать ситуации, в которых численные методы дают преимущество. Обучающиеся проверяют гипотезы, сопоставляют альтернативные методы и формируют осознанный выбор подхода к решению задач. Освоение этих навыков развивает критическое мышление – способность оценивать данные, выявлять закономерности и принимать обоснованные решения, укрепляет исследовательскую самостоятельность и формирует системный, осознанный подход к научному исследованию, углубляя понимание того, как и когда применять численные методы для решения практических и теоретических задач.
Освоение вероятностного подхода к анализу данных. Работа с методом Монте-Карло вводит обучающихся в вероятностную природу моделируемых процессов и побуждает рассматривать результаты с учетом случайности и вариативности данных. В ходе экспериментов обучающиеся анализируют распределения, отслеживают изменения выборок, оценивают устойчивость результатов и учатся связывать наблюдаемые частоты с вероятностями событий. Такой опыт делает случайность не абстрактным понятием, а инструментом анализа, встроенным в решение практических и теоретических задач. В результате формируется вероятностное мышление – способность понимать поведение случайных процессов, интерпретировать вероятностные характеристики и опираться на статистические закономерности при анализе данных и принятии решений.
Повышение мотивации через практико-ориентированное исследование. Практическое использование метода Монте-Карло делает учебный процесс более наглядным и содержательным: абстрактные математические идеи приобретают конкретную форму через моделирование, эксперименты и визуализацию результатов. Обучающиеся видят прямую связь между теорией и ее применением в реальных задачах – от анализа неопределенности до изучения сложных систем. Работа с моделями усиливает чувство вовлеченности, формирует интерес к исследовательской деятельности и повышает уверенность в собственных возможностях. Такой опыт создает устойчивую учебную мотивацию и делает освоение материала осмысленным и личностно значимым.
Заключение
В ходе исследования была достигнута цель – выявлены дидактические функции метода Монте-Карло, которые могут способствовать формированию у студентов аналитического, алгоритмического и вероятностного мышления при изучении математических дисциплин.
Анализ научной и учебно-методической литературы позволил систематизировать представления об алгоритме метода Монте-Карло, выделить его основные этапы и уточнить особенности применения в образовательной среде. На этой основе определены ключевые дидактические функции метода, связанные с развитием навыков математического моделирования, интерпретацией результатов стохастических процедур и освоением принципов работы со случайностью в вычислительных задачах.
Применение метода Монте-Карло в учебном процессе усиливает познавательную мотивацию студентов и делает освоение материала более личностно значимым, поскольку основано на самостоятельном поиске решений, экспериментировании и осмысленном взаимодействии с математическими моделями
Конфликт интересов
Библиографическая ссылка
Григорян М.Э. ДИДАКТИЧЕСКИЕ ФУНКЦИИ МЕТОДА МОНТЕ-КАРЛО ПРИ ИЗУЧЕНИИ МАТЕМАТИЧЕСКИХ ДИСЦИПЛИН В ВЫСШЕЙ ШКОЛЕ // Современные проблемы науки и образования. 2025. № 6. ;URL: https://science-education.ru/ru/article/view?id=34386 (дата обращения: 07.01.2026).
DOI: https://doi.org/10.17513/spno.34386



