Введение
В 2022 году средние общеобразовательные школы перешли на новый Федеральный государственный образовательный стандарт основного общего образования третьего поколения [1]. Основные изменения стандарта коснулись целей и требований к результатам обучения (личностным, метапредметным и предметным). В качестве одной из целей основного образования определено овладение обучающимися приемами реализации учебно-исследовательской деятельности. Метапредметные результаты обучения представлены в виде трех групп универсальных учебных действий.
Группа познавательных универсальных учебных действий (ПУУД), состоящая из логических действий, исследовательских действий и действий с информацией, отражает содержание учебно-исследовательской деятельности (УИД) на разных ее этапах. Поэтому естественно предположить, что начальным этапом процесса формирования навыков выполнения учебно-исследовательской деятельности у обучающихся должен стать этап формирования отдельных ПУУД.
Математика как учебная дисциплина обладает значительным дидактическим потенциалом для реализации учебных исследований школьников. Самостоятельное решение любой субъективно новой математической задачи является для обучающегося исследованием, требующим поэтапного выполнения УИД. Действительно, «математика непосредственно способствует развитию когнитивных способностей обучающихся, прививает навыки построения и исследования математических моделей реальных объектов и процессов» [2, с. 59]. Поэтому математику рассматриваем в качестве предметной области для формирования навыков учебно-исследовательской деятельности школьников.
Цель исследования – разработать, научно обосновать и экспериментально проверить содержание компонентов модели методики формирования навыков учебно-исследовательской деятельности через систему ПУУД у обучающихся основной школы на уроках математики.
Материал и методы исследования. Теоретической основой для разработки методики формирования навыков учебно-исследовательской деятельности через систему ПУУД послужили основные положения теории поэтапного формирования умственных действий П.Я.Гальперина [3], учение о типах ориентировочной основы деятельности Н.Ф.Талызиной[4], труды ученых по формированию метапредметных результатов обучения (Л.И. Боженкова[5], Е.О. Новикова, И.Н. Власова [6], Е.В. Позднякова, Г.А. Малышенко [7]идр.). Труды психологов и методистов-математиков по развитию учебно-исследовательской деятельности (Т.А. Воронько [8], В.А. Далингер [9], М.В.Таранова [10], К.А. Халатян [11]идр.) были использованы для уточнения сущностных характеристик понятия «учебно-исследовательская деятельность», для создания плана формирования навыков УИД в основной школе, для разработки средств и методов обучения.
Опытно-экспериментальная работа по проверке эффективности разработанной авторами методики была проведена в период 2021–2024 гг. с обучающимися 7–8-х классов государственного бюджетного образовательного учреждения Астраханской области «Школа одаренных детей им. А.П. Гужвина». Целью эксперимента на основном этапе (соответствующем возрастной категории обучающихся) стратегического плана формирования учебно-исследовательских умений являлось формирование навыков реализации отдельных этапов УИД.
Результаты исследования и их обсуждение. На основе анализа определений разных авторов в контексте настоящего исследования уточнено содержание понятия «учебно-исследовательская деятельность», под которой будем понимать вид учебно-познавательной поисковой деятельности обучающихся, который реализуется в соответствии с основными этапами исследования и способствует формированию навыков выполнения учебно-исследовательской деятельности[12].
Для целостного представления о процессе формирования учебно-исследовательских умений обучающихся основной школы при обучении математике разработана модель методики, в основу которой положено установленное авторами соответствие между этапами реализации УИД и выполнением ПУУД (рис.1).
В модели выделены целевой, теоретический, содержательный, процессуальный и контрольно-корректировочный блоки. Перечисленные компоненты образуют систему, взаимосвязаны и функционируют как единое целое. Раскроем сущность каждого блока.
Целевой блок модели включает в себя цель, которая определяет ожидаемый результат и задает направление деятельности учителя и обучающихся. Целью реализации построенной модели является переход большинства обучающихся на более высокий уровень сформированности учебно-исследовательских умений.
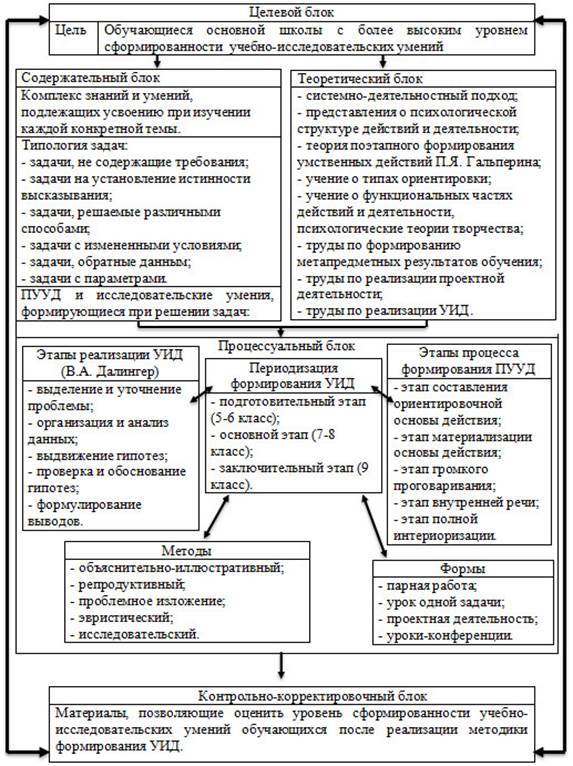
Рис. 1. Модель методики формирования учебно-исследовательских умений обучающихся через систему ПУУД при обучении математике
Теоретический блок модели содержит описанные выше теоретические основы исследования.
Процессуальный блок рассматриваемой модели включает в себя методику формирования навыков УИД обучающихся основной школы на уроках математики в соответствии со следующими этапами:
- этапы плана формирования навыков УИД, соответствующие возрастным особенностям обучающихся (табл. 1);
- этапы реализации УИД [10];
- этапы формирования ПУУД [4, 5, 6].
Таблица 1
План формирования навыков УИД в основной школе
|
Этап формирования навыков УИД |
Период |
Цель этапа |
Средства формирования |
|
Подготовительный этап |
5–6-й класс |
Сформировать ПУУД, входящие в состав учебно-исследовательской деятельности |
Задачи, направленные на формирование ПУУД |
|
Основной этап |
7–8-й класс |
Сформировать навыки реализации этапов учебно-исследовательской деятельности |
Учебно-исследовательские задачи |
|
Заключительный этап |
9-й класс |
Сформировать навыки реализации учебно-исследовательской деятельности как целостного процесса |
Проектные задания |
Содержательный блок модели включает:
– комплекс дидактических средств для изучения каждой конкретной темы, разработанный в соответствии с типологией задач Т.А. Воронько [9];
– установленное авторами соответствие между ПУУД и учебно-исследовательскими умениями, формирующимися при решении задач [12]. Например, для овладения учебно-исследовательским умением «выделение и уточнение проблемы исследования» у обучающихся должны быть сформированы следующие познавательные универсальные учебные действия: использовать вопросы как исследовательский инструмент познания, формулировать вопросы, фиксирующие разрыв между реальным и желательным состоянием ситуации, объекта; самостоятельно устанавливать искомое и данное; с учетом предложенной задачи выявлять закономерности и противоречия в рассматриваемых фактах, данных и наблюдениях; предлагать критерии для выявления закономерностей и противоречий.
В качестве примеров содержательного обеспечения методики формирования учебно-исследовательских умений представлены образцы дидактических материалов для изучения темы «Линейная функция» в 7-м классе: схема определения основного понятия (рис. 2); примеры задач, разработанные в соответствии с типологией учебно-исследовательских задач Т.А.Воронько (табл. 2).

Рис. 2. Схема определения понятия «линейная функция»
Таблица 2
Примеры учебно-исследовательских задач по теме «Линейная функция»
|
Тип задачи |
Пример задачи |
|
Задачи, не содержащие требования |
Составьте различные требования к условию задачи и решите полученные задачи. Функции заданы формулами: а) у = 2х; у = 2х + 2; у = 2х + 4; у = 2х – 1; б) у = 3; у = -х + 3; у = х + 3; у = -2х + 3. |
|
Задачи на установление истинности высказывания |
Верно ли утверждение: 1. Если угловые коэффициенты линейных функций равны, то их графики не пересекаются. 2. Если угловой коэффициент положительный, то угол наклона графика линейной функции к положительному направлению оси х острый. 3. Прямая пропорциональность является частным случаем линейной функции. 4. Линейная функция является частным случаем прямой пропорциональности. Приведите контрпримеры, доказывающие ложность следующих утверждений: 1. Любая прямая является графиком линейной функции. 2. Горизонтальная прямая не является графиком линейной функции. 3. График линейной функции пересекает ось Ох в единственной точке |
|
Задачи с некорректными условиями |
а) Задачи с недостающими данными: Найдите формулу задания линейной функции, проходящей через точку М(2; -3). б) Задачи с избыточными данными: Задайте формулой прямую пропорциональность, график которой параллелен прямой у = 3х – 4 и проходит через точки А (1; 3); В (4; 12) |
|
Обратные задачи |
Решите данную задачу. Составьте и решите задачу, обратную данной: Линейная функция пересекает оси координат в точках (0; 2) и (-1; 0). Найдите формулу задания этой функции |
|
Задачи с параметрами |
Дана линейная функция у = ах + 4. При каком значении а график этой функции: а) параллелен графику прямой пропорциональности у = 3х; б) пересекает ось ординат в точке с ординатой 4 |
Контрольно-корректировочный блок модели представлен материалами, позволяющими оценить уровень сформированности навыков УИД в процессе педагогического эксперимента: уровни сформированности, задания входной и итоговой контрольных работ, критерии их оценивания. Поскольку педагогический эксперимент был проведен в 7–8-х классах, что соответствует основному этапу развития навыков УИД (табл.1), то оценивалась способность обучающихся выполнять отдельные этапы УИД при решении задач.
Примеры заданий входной и итоговой контрольных работ, показатели и критерии их оценивания представлены в таблице 3.
Таблица 3
Примеры заданий контрольной работы и критерии их оценивания
|
Задания контрольной работы |
Показатели сформированности навыков УИД |
Критерии оценивания |
|
1. Составьте различные требования к данному описанию и решите полученные задачи. «При подготовке к экзамену ученик планировал ежедневно решать 12 задач. Однако он решал ежедневно на 4 задачи больше. Когда до экзамена осталось 2 дня, ему осталось решить 6 задач» |
Выделение и уточнение проблемы |
5 баллов за каждую правильно составленную и решенную задачу; 2 балла за каждую правильно составленную, но не решенную задачу |
|
2. Дайте обоснованный ответ на вопрос, не решая задачу аналитически: «Существует ли такое значение аргумента х, при котором значения функций |
Выдвижение гипотез |
5 баллов за правильно решенную задачу |
|
3. Сформулируйте утверждение, обратное данному. Установите истинность или ложность прямого и обратного утверждений: «Если треугольник равносторонний, то его углы равны» |
Проверка и обоснование гипотез |
3 баллов за правильно сформулированную и решенную задачу; 2 балла за правильно сформулированную, но не решенную задачу |
Для исследования динамики формирования навыков учебно-исследовательской деятельности в экспериментальных и контрольных классах были проведены входная и итоговая контрольные работы. Анализ результатов педагогического эксперимента показал, что в экспериментальных классах, обучение в которых осуществлялось по авторской методике, наблюдались снижение долей обучающихся с низким и средним уровнями сформированности выделенных авторами навыков УИД (в среднем на 18%) и увеличение долей обучающихся с высоким и творческим уровнями сформированности навыков УИД. При этом в контрольном классе произошли незначительные изменения в уровнях сформированности у обучающихся навыков УИД (в среднем на 5%).
Выводы. Установленное соответствие между этапами учебно-исследовательской деятельности и познавательными универсальными учебными действиями, необходимыми для их реализации, позволило разработать методику формирования навыков учебно-исследовательской деятельности на уроках математики в основной школе. Экспериментальные данные позволяют сделать вывод, что представленная методика обеспечивает положительную динамику уровней сформированности навыков учебно-исследовательской деятельности при обучении математике. Методически верно организованный процесс обучения математике в основной школе последовательно подготовит ее выпускников к самостоятельному участию в проектной деятельности, успешному решению практико-ориентированных задач и задач повышенной сложности, будет способствовать формированию первичного исследовательского опыта и научного мировоззрения.
Библиографическая ссылка
Астахова Т.Н., Бурмистрова Н.А., Байгушева И.А. МОДЕЛЬ МЕТОДИКИ ФОРМИРОВАНИЯ НАВЫКОВ УЧЕБНО-ИССЛЕДОВАТЕЛЬСКОЙ ДЕЯТЕЛЬНОСТИ ОБУЧАЮЩИХСЯ ОСНОВНОЙ ШКОЛЫ НА УРОКАХ МАТЕМАТИКИ // Современные проблемы науки и образования. 2025. № 1. ;URL: https://science-education.ru/ru/article/view?id=33901 (дата обращения: 13.03.2026).
DOI: https://doi.org/10.17513/spno.33901




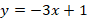 и
и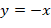 равны?»
равны?»