Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Введение

Широкое внедрение современных форм государственной итоговой аттестации обучающихся по учебным предметам, в частности основного государственного экзамена и единого государственного экзамена по математике, приводит к необходимости совершенствования на основе их результатов методики обучения математике в школе [1, c. 26]. Результаты этих экзаменов подвергаются тщательному анализу на различных уровнях образования: класса, школы, региона, страны [2, c. 14]. Особенный интерес представляют предметные результаты обучения математике по различным блокам учебного содержания [3, с. 23].

Данные объективных процедур контроля знаний позволяют характеризовать качество математического образования в его динамике [4, с. 32].

Цель исследования – изучение динамики предметных результатов обучения выражениям и преобразованиям на основе количественных и качественных данных основного государственного и единого государственного экзамена по математике в одном из регионов Российской Федерации – Алтайском крае.

Материал и методы исследования

В ходе исследования предстояло выявить количественные и качественные данные предметных результатов обучения обучающихся одному из разделов учебного материала – «Выражения и преобразования», на основе изучения данных основного государственного экзамена по математике и единого государственного экзамена профильного уровня. Для этого использованы теоретические и эмпирические методы: анализ, синтез, обобщение. На втором этапе с помощью экспертных оценок выявлялись погрешности в предметных результатах обучения этому разделу, возможные причины появления ошибок и пути их предотвращения [5, c. 36]. Исследование проводилось с использованием материалов региональной предметной комиссии по проверке задач с развернутым ответом государственной итоговой аттестации по математике в Алтайском крае.

Результаты исследования и их обсуждение

Исходные положения.

1. Раздел «Выражения и преобразования» относится в основном к дисциплине «Алгебра» школьного курса математики. Его усвоение проверяется в условиях ОГЭ и ЕГЭ по математике профильного уровня в виде как заданий с кратким ответом, так и задач с развернутым решением.

2. По результатам итоговой государственной аттестации на уровне региона возможно выявление погрешностей участников экзамена, в том числе ошибок, в частности типичных ошибок. Сравнение данных результатов ОГЭ и ЕГЭ, продемонстрированных одним и тем же контингентом участников, позволяет выявить повторяющиеся ошибки, а также погрешности, которые были исправлены в процессе обучения в старшей школе.

3. На основе сравнения данных ОГЭ и ЕГЭ по математике могут быть выделены элементы содержания и характеристики учений, характеризующиеся положительной динамикой результатов.

4. Основным объектом оценки предметных результатов обучения является достижение обучающимися планируемых результатов обучения: способность обучающихся решать учебно-познавательные и учебно-практические задачи с использованием средств, релевантных учебному предмету, в том числе на основе метапредметных действий [6, c. 12].

Материал блока учебного содержания «Выражения и преобразования» занимает центральное место в школьном курсе математики, так как формирует базовые навыки алгебраических преобразований, необходимые для последующего изучения более сложных математических концепций. Понимание методов преобразования выражений помогает обучающимся не только решать уравнения, но и развивает аналитическое мышление, что является важным аспектом общего образования. Процесс преобразования выражений включает в себя использование различных алгебраических правил и свойств, таких как распределительный и сочетательный законы, приведение подобных членов в выражениях, упрощение выражений, сокращение дробей и др. Эти приемы не только упрощают решения задач, но и способствуют глубинному пониманию структуры математических отношений. Школьники учатся распознавать паттерны и связи между величинами, что в дальнейшем помогает им в изучении различных областей математики, включая геометрию и анализ.

Кроме того, навыки работы с выражениями имеют практическое применение в инженерии, физике и экономике. Таким образом, изучение преобразования выражений не только обогащает математическую подготовку, но и открывает возможности для продолжения образования.

В процессе контроля предметных результатов обучения математике в условиях итоговой аттестации целесообразно придерживаться следующих принципов: достоверность, объективность и информативность оценки [7, c. 23]. Ориентация на достижение планируемых результатов должна пройти через все составляющие и все виды оценивания.

Данные о предметных результатах освоения блока учебного содержания «Выражения и преобразования» были получены из анализа представленных в таблице 1 заданий ОГЭ-2022 и ЕГЭ-2024 по математике профильного уровня.

Таблица 1

Требования к результатам выполнения заданий

Общая динамика результатов, демонстрируемых участниками ЕГЭ по математике профильного уровня, показана в таблице 2.

Таблица 2

Результаты ЕГЭ по математике профильного уровня

Сравнение результатов показывает положительную динамику выполнения заданий, проверяющих результаты освоения содержания раздела (рис. 1).

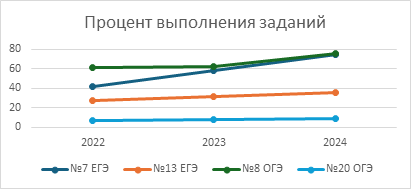
Рис. 1. Процент выполнения заданий

Важным для совершенствования обучения становится выявление погрешностей в предметных результатах обучения школьников. Эта проблема различными способами решается в научно-педагогической и методической литературе [8-10].

Особенностью ОГЭ и ЕГЭ по математике является наличие двух типов задач: с кратким ответом и с развернутым ответом. Выводы о погрешностях при выполнении задач с кратким ответом носят вероятностный характер и делаются на основе анализа вееров ответов участников экзамена. Термин «веер ответов» [11, с. 425] применительно к заданию контрольно-измерительных материалов экзамена означает множество всех ответов, которые участники экзамена предоставили в результате его выполнения. В качестве примера рассмотрим затруднения обучающихся при выполнении одного из заданий ЕГЭ по математике.

Задание 1. Найдите значение выражения .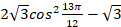

Приступили к решению этой задачи 88,92% участников экзамена. Верный ответ «1,5» получили 168 человека, что составляет 42,97%. «Массовые» неверные ответы: «2» (получили 25 участников экзамена), «0» (24 человека), «1» (23 человека).

Типичная ошибка, приведшая обучающихся к неправильным ответам, указывает на неправильное оперирование действиями над тригонометрическими выражениями, незнание тригонометрических формул и значений тригонометрических функций острых углов.

При анализе решений школьниками заданий с развернутым ответом учитывались требования к оцениванию стандартных задач [12, c. 43]. Такой анализ позволяет выявить типичные ошибки и затруднения обучающихся. Рассмотрим одну из таких задач.

Задание 2

а) Решите уравнение .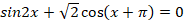

б) Укажите корни этого уравнения, принадлежащие отрезку [].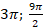

Решаемость задания 2 представлена на рисунке 2.

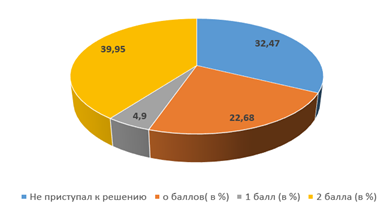
Рис. 2. Процент решаемости задачи 2

Типичные ошибки при решении задания 2

1. Уравнение в задании решалось разложением на множители, предварительно использовались формула синуса двойного угла и формулы приведения. В целом, можно констатировать слабое владение обучающихся этим методом решения уравнения, несформированность необходимых алгоритмов.

2. Ошибки при применении формул приведения.

3. Деление обеих частей уравнения на выражение с переменной, которое в этой задаче может быть равно нулю. Обучающиеся часто делили обе части уравнения на 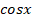, теряя при этом отдельные корни уравнения.

4. Нередко, решая простейшее тригонометрическое уравнение, обучающиеся находили неверное его решение.

Ежегодно среди типичных ошибок участников ЕГЭ по математике при решении такой задачи констатируется незнание формул раздела «Тригонометрия» школьного курса математики: корней простейших тригонометрических уравнений общего и частного вида, табличных значений тригонометрических и обратных тригонометрических функций и др. Наиболее типичными среди них в 2024 году были ошибки в формулах корней простейших тригонометрических уравнений общего или частного вида, незнание формул приведения и табличных значений обратных тригонометрических функций.

При отборе корней в пункте б) задачи 2 многие участники ЕГЭ не оформляют решение должным образом. Часто обоснование ответа не является полным или совсем отсутствует.

В зависимости от способа отбора корней из промежутка часто встречалась одна из следующих ситуаций:

· осуществляется перебор целых значений k без обоснования, почему другие значения рассматривать не нужно;

· на единичной окружности не выделен исследуемый промежуток или указаны корни, не принадлежащие данному промежутку.

Отсутствие обоснования решения при отборе корней, даже при правильном ответе, не позволяет эксперту оценить пункт б) задания 2 положительным баллом.

Следует отметить, что при решении задачи 2 обучающиеся традиционно и в основном успешно использовали различные способы отбора корней: перебор, с помощью двойного неравенства, используя единичную окружность.

Информативность оценивания результатов государственной итоговой аттестации обеспечивается выявлением погрешностей участников экзамена и планированием предупреждающих и корректирующих действий [13-15].

Рассматриваемые погрешности обучающихся согласуются с опытом современной подготовки к ОГЭ по математике [16; 17].

Выводы

Сопоставление результатов ОГЭ и ЕГЭ в Алтайском крае позволило выявить положительную динамику предметных результатов обучения выражениям и преобразованиям. Типичные ошибки обучающихся встречаются при выполнении как задач с кратким, так и с развернутым ответом. Выявление таких ошибок позволяет обосновать рекомендации по совершенствованию организации и методики преподавания учебного предмета «Математика» всем обучающимся.

На основе анализа результатов итоговой государственной аттестации разработана методика анализа выполнения заданий ОГЭ и ЕГЭ по математике профильного уровня, включающая:

а) выявление погрешностей при выполнении заданий контрольно-измерительных материалов;

б) оформление форм представления результатов;

в) контроль предметных результатов обучения математике в условиях итоговой аттестации;

г) типизацию ошибок при выполнении заданий экзаменов.

Подготовку к ОГЭ по математике целесообразно осуществлять по направлениям: информационная деятельность, психолого-педагогическое и методическое сопровождение, повышение предметных и методических компетенций учителей.

Заключение

Динамика предметных результатов обучения математике представляет собой сложный и многоуровневый процесс, который включает в себя как количественные, так и качественные изменения в понимании и освоении математических концепций учениками. Важным аспектом этой динамики является учет возрастных и индивидуальных особенностей обучающихся, их предшествующего опыта и мотивации к обучению.

Систематический подход к анализу результатов обучения позволяет выявить закономерности, влияющие на рост учебных достижений обучающихся. Сопоставление результатов ОГЭ и ЕГЭ позволяет в динамике отследить усвоение различных разделов предмета, в частности блока «Выражения и преобразования», что демонстрирует практика осуществления аналитической работы по результатам экзамена.

Кроме того, значительную роль в динамике предметных результатов играет интеграция математических знаний с другими дисциплинами. Это помогает ученикам понять практическую ценность математики и ее применение в реальной жизни. Опыт показывает, что в результате обучающиеся становятся более уверенными в своих силах и способны к самостоятельному анализу и обобщению информации, что положительно сказывается на их учебных успехах.