Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Введение. Имплантация современных интраокулярных линз (ИОЛ) позволяет офтальмологам успешно решать задачи по хирургическому лечению катаракты. При этом улучшение зрительных функций пациента напрямую связано с точностью предоперационного расчета оптической силы ИОЛ. К настоящему времени разработано значительное количество формул для расчета данного показателя, отличающихся принципиальным подходом (теоретический, аппроксимационный, базируемый на машинном обучении и системах искусственного интеллекта), числом входных параметров и коэффициентов, а также количеством данных в датасете, на которых были получены эти коэффициенты.

Поколения формул для расчета оптической силы ИОЛ. Первая формула расчета оптической силы ИОЛ была создана академиком С.Н. Федоровым с сотрудниками в 1967 году. Эта формула была основана на законах физической оптики, то есть на теоретических представлениях преломления пучка света оптическими средами глаза. В связи с этим данная формула и созданные позже, основанные на законах физиологической оптики, получили название теоретических. Данные формулы обычно относят к первому поколению.

Формулы второго поколения основаны на обработке больших массивов эмпирических данных и по своей сути являются регрессионными, т.е. не несут в себе теоретической базы, но хорошо соответствуют наблюдениям.

Формулы третьего поколения являются смешанными, т.е. сочетают в себе известные теоретические положения, а их коэффициенты оптимизированы на основе больших массивов эмпирических данных.

И, наконец, формулы четвертого поколения появились в связи с быстрым развитием систем искусственного интеллекта, базируемого на искусственных нейронных сетях. Такой подход сочетает в себе гибкость в выборе архитектуры модели или структуры формулы с легкостью получения значений коэффициентов формул на основе датасетов эмпирических данных с использованием алгоритмов машинного обучения.

Имеются работы, в которых проведено сравнение классических формул для расчетов оптической силы ИОЛ [1–3], а также исследуется целесообразность использования для этой цели современных систем искусственного интеллекта, основанных на машинном обучении [4–6].

Работа T. Yamauchi с соавт. [7] посвящена исследованию использования машинного обучения для прогнозирования возникновения послеоперационной рефракции после операции по удалению катаракты и сравнению точности этого метода с традиционными формулами расчета оптической силы интраокулярной линзы. Всего был исследован 3331 глаз от 2010 пациентов. При этом коэффициенты формул расчета оптической силы ИОЛ и модели машинного обучения были оптимизированы с использованием обучающих данных, т.е. адаптированы к локальным данным. Были оценены результаты, полученные по формулам SRK/T, Haigis, Holladay 1, Hoffer Q и Barrett Universal II. Показано, что среди традиционных формул Barrett Universal II имела самую низкую среднюю и медианную абсолютную ошибку прогноза. Поэтому авторы сравнили точность моделей машинного обучения с точностью Barrett Universal II. Абсолютные ошибки некоторых методов машинного обучения были ниже, чем у Barrett Universal II. Однако статистически значимой разницы не наблюдалось. Авторы сделали вывод, что точность методов машинного обучения не уступала точности формулы Barrett Universal II.

В обзоре W. Stopyra с соавт. [1] оценивали точность формул для расчета оптической силы ИОЛ, основанных на искусственном интеллекте, на основе анализа статей, опубликованных с 2017 года по июль 2023 года. Всего было рассмотрено 25 рецензируемых статей на английском языке с максимальной выборкой и наибольшим количеством сравниваемых формул. Для оценки точности формул использовали оценки средней абсолютной ошибки и процента пациентов, для которых рефракционная ошибка расчета попадала в диапазоны ±0,5 дптр и ±1,0 дптр. В большинстве случаев формула Kane позволила получить наименьшую среднюю абсолютную ошибку и самый высокий процент пациентов в указанных диапазонах. Второе место обычно занимала формула Pearl DGS.

N. Kuthirummal с соавт. [4] считают, что формула Barrett Universal II (BU-II) является одной из наиболее точных современных формул расчета оптической силы линз. Основной акцент исследования сделан на том, чтобы оценить возможности этой формулы и ее точность в прогнозировании оптической силы ИОЛ при хирургии катаракты у азиатско-индийской популяции, т.е. оценить возможности ее локализации. Необходимость локализации формулы может быть вызвана различием измерительных приборов, некоторым отличием используемых методик измерения, а также и спецификой пациентов.

В современной офтальмологической практике наиболее часто используются как формулы третьего поколения, так и формулы четвертого поколения, разработанные с использованием систем искусственного интеллекта. Необходимо отметить, что формулы третьего поколения и их коэффициенты можно найти в специальной литературе или на соответствующих сайтах. Это означает, что возможно осуществить локализацию этих формул на основании датасетов определенного региона или даже клиники, путем оптимизации их параметров на основе методов нелинейного программирования, как это сделано, например, в работах T. Yamauchi с соавт. [7] или А.А. Арзамасцева с соавт. [8]. Формулы четвертого поколения обычно представлены в виде специализированных калькуляторов, например: https://iolcalculator.escrs.org/. По этой причине любые их модификации практически исключены.

Наиболее популярными среди офтальмологов являются формулы второго и третьего поколений SRK II, Haigis, Holladay, SRK/T. Несмотря на существенные погрешности расчетов по этим формулам, офтальмологи «привыкли» к их использованию и часто расчетную величину корректируют при помощи «своей добавки», которую они получили эмпирически, учитывая большой опыт работы. По всей видимости, формулы четвертого поколения, такие как Barrett Universal II, Hill-RBF, Kane, Pearl DGS, судя по данным обзора [1], в такой «добавке» не нуждаются или нуждаются в ней в значительно меньшей степени.

Целью исследования является сравнение точности расчетов оптической силы интраокулярных линз с использованием формул различных поколений, в том числе и основанных на системах искусственного интеллекта, на локальных данных одной из офтальмологических клиник.

Материалы и методы исследования. При сравнении погрешностей различных поколений формул для расчета оптической силы ИОЛ рассчитывались следующие основные показатели: средняя относительная погрешность, выраженная в процентах, и процент попадания расчетных величин оптической силы ИОЛ в диапазон ±0,5 дптр от требуемого значения (послеоперационная эмметропия). Дополнительными показателями являлись: абсолютная погрешность и ее распределение по диапазонам; максимальная относительная погрешность формул, характеризующая их адаптивность к крайним значениям параметров.

Погрешности формул второго и третьего поколений SRK II, Haigis, Holladay, SRK/T анализировались на основании значительного количества эмпирических данных, предоставленных в обезличенном виде Тамбовским филиалом МНТК «Микрохирургия глаза» им. академика С.Н. Федорова [8]. Начальное количество записей 28940. Запись в таблице содержит следующие параметры: условный номер пациента, дату операции, марку и оптическую силу установленной линзы, возраст, длину глаза, необходимую оптическую силу линзы для коррекции аномалии рефракции и астигматизма (сфера, цилиндр), а также некоторую дополнительную информацию, связанную с положением линзы в глазу. Количество обработанных записей – 11701. Были исключены 17239 записей по следующим причинам: не известны параметры линзы, очевидно некорректные данные в полях (например, на несколько порядков превышающие средние значения).

Поскольку в работе А.А. Арзамасцева с соавт. [8] не анализировался процент попадания расчетных величин оптической силы ИОЛ в диапазон ±0,5 дптр от требуемого значения, эти параметры восстанавливали для сравнения с аналогичными параметрами формул четвертого поколения путем вычислительного эксперимента, в котором учитывались известные показатели: распределение абсолютных ошибок (общий вид зависимости) и средняя относительная погрешность формулы.

Погрешности формул четвертого поколения Barrett Universal II, Hill-RBF, Kane, Pearl DGS и процент попадания расчетных величин оптической силы ИОЛ в диапазон ±0,5 дптр от требуемого значения рассчитывали на основании сравнения таблицы эмпирических значений, предоставленных в обезличенном виде Тамбовским филиалом МНТК «Микрохирургия глаза» им. академика С.Н. Федорова, и вычислениями по соответствующим калькуляторам https://iolcalculator.escrs.org/. Расчеты были сделаны сначала на датасете в 150 записей, а затем на датасете в 400 записей, после чего произвели сравнение полученных результатов. Использование такой технологии было необходимо для подтверждения репрезентативности выборки ввиду небольшого количества записей.

Результаты исследования и их обсуждение. Формулы второго и третьего поколений. На рисунке1 приведены корреляционные зависимости необходимой (эмметропия) и расчетной оптической силы ИОЛ по формулам SRK II, Haigis, Holladay, SRK/T [8].

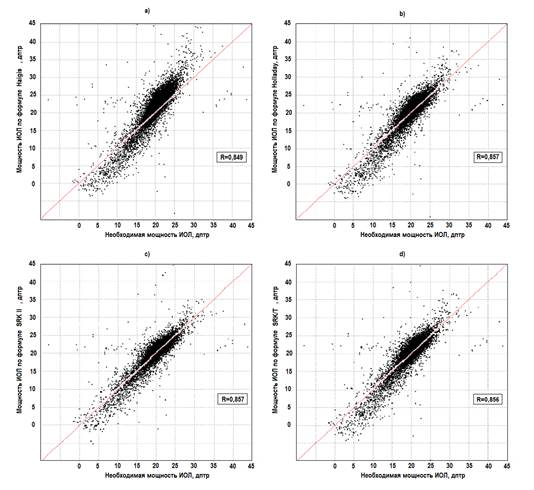
Рис. 1. Корреляционные зависимости необходимой мощности ИОЛ (эмметропия) по оси абсцисс и расчетное значение мощности ИОЛ – по оси ординат по формулам: a) – Haigis, b) – Holladay, c) – SRK II, d) – SRK/T для 11701 пациента. Значения коэффициентов корреляции приведены на графиках

Видно, что для средних значений оптической силы ИОЛ все формулы дают близкие к необходимым результаты, однако при крайних значениях наблюдается значительный разброс относительно необходимых значений. На рисунках 1 a), b) и d) наблюдается также значительное несовпадение угла наклона зависимостей относительно диагонали, соответствующей точным расчетам. Все исследованные формулы в качестве входных величин используют всего три параметра: AL – длина глаза, мм; K – среднеарифметическое преломляющей силы сильного и слабого меридианов роговицы (или радиусов передней поверхности роговицы), мм; ACD (константа А и т.п.) – параметр линзы, задаваемый производителем. Это обстоятельство невольно наводит на мысль, что существуют другие факторы (возможно, ненаблюдаемые), воздействие которых на оптическую силу ИОЛ приводит к перечисленным особенностям расчета. Средние относительные погрешности формул второго и третьего поколений, полученные на значительных выборках эмпирических данных, составляют 11,7–15,6%, при этом процент попадания расчетных величин оптической силы ИОЛ в диапазон ±0,5 дптр от требуемого значения является очень низким и составляет 11–14% (табл.). Данное обстоятельство как раз и оправдывает тот факт, что многие практикующие офтальмологи при использовании этой группы формул корректируют полученные результаты с помощью некоторых «добавок», полученных по результатам многолетнего опыта.

В работе А.А. Арзамасцева с соавт. [8] для этих же эмпирических данных авторы привели оптимизированную регрессионную формулу, полученную в результате решения задачи оптимизации коэффициентов. В ней удалось снизить среднюю относительную погрешность до 10,6% и, соответственно, получить процент попаданий в диапазон ±0,5 дптр на уровне 18%.

Для формул второго и третьего поколений, а также для оптимизированной регрессионной формулы процент попаданий рассчитывался на основе вычислительного эксперимента, результаты которого представлены в виде аппроксимационной кривой на рисунке 2. Кривая имеет гладкий характер, что может свидетельствовать о ее адекватности как эмпирическим данным, так и различным формулам, используемым для расчетов оптической силы ИОЛ.

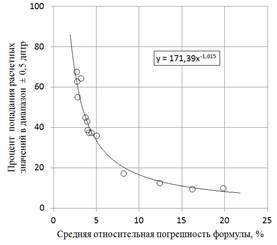
Рис. 2. Аппроксимация зависимости процента попадания расчетных значений оптической силы ИОЛ по различным формулам в диапазон ±0,5 дптр от средней относительной погрешности формулы

Таким образом, анализ результатов расчетов величин оптической силы ИОЛ с помощью формул второго и третьего поколений на локальных данных показал их значительные погрешности, что могло быть вызвано учетом лишь главных входных факторов. Очевидно, что увеличение числа входных факторов, доступных офтальмологу перед операцией, должно снизить погрешности формул и, как следствие, увеличить процент попадания расчетных величин в диапазон ±0,5 дптр, что авторы и наблюдают у формул четвертого поколения.

Формулы четвертого поколения. Поскольку выборка локальных эмпирических данных, имеющихся в распоряжении авторов для проверки погрешностей формул четвертого поколения, была относительно мала (400 записей), была предпринята попытка оценки репрезентативности такой выборки. Для этой цели оценки средней относительной погрешности и процента попаданий расчетной величины в диапазон ±0,5 дптр проводили сначала на случайной выборке из 150 записей, а затем эти же параметры получали для всех 400 записей. Полученные значения практически совпали, что указывает на репрезентативность выборки, состоящей из 400 записей. Далее проводили оценку точности каждой из формул четвертого поколения путем сравнения расчетных и эмпирических данных. Так, на гистограммах (рис. 3) показан разброс абсолютных ошибок формул Barrett Universal II, Hill-RBF, Kane и Pearl DGS. Видно, что распределение ошибок близко к нормальному закону. При оценке процента попаданий в диапазон ±0,5 дптр лучшие результаты показала формула Barrett Universal II (68%). В обзоре [1] на основе анализа значительного числа литературных источников эта цифра составляет 75%. Другие формулы дают меньший процент попаданий в указанный диапазон (табл.). Интересно отметить тот факт, что на локальных данных из всех формул четвертого поколения наименьший процент попаданий в диапазон у формулы Kane (55%), которая в ряде литературных источников часто называется одной из лучших в смысле точности на настоящий момент. Данное обстоятельство может указывать на существование некоторых особенностей локальных выборок данных.

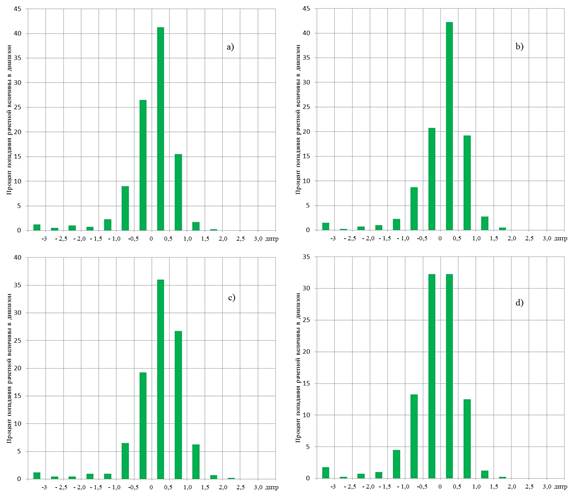
Рис. 3. Гистограммы распределений абсолютных погрешностей различных формул четвертого поколения (дптр): a)Barrett Universal II, b) Hill-RBF, c) Kane, d) Pearl DGS

Для визуализации точности аппроксимации эмпирических данных на рисунках 4–7 показаны корреляционные зависимости расчетной величины оптической силы ИОЛ по оси ординат от требуемого значения (эмметропия) по оси абсцисс. Если формулы были бы абсолютно точными, то все точки на этих графиках ложились бы точно на диагональ квадрата. Их отклонение от этой диагонали визуализирует ошибку формулы. Можно сделать вывод, что все исследованные формулы дают близкие значения оптической силы ИОЛ, однако расчет средней относительной погрешности (табл.) свидетельствует о том, что наиболее точные результаты получаются по формуле Barrett Universal II. У этой формулы также и самое маленькое значение максимальной относительной погрешности (табл.), что может быть свидетельством ее хорошей адаптивности к крайним значениям параметров.

В таблице показаны также входные параметры, учитываемые каждой из формул различных поколений при расчете оптической силы ИОЛ.

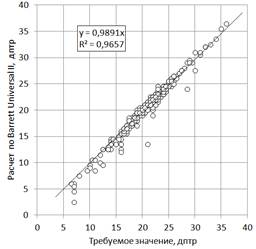
Рис. 4. Значения оптической силы ИОЛ, рассчитанные по формуле Barrett Universal II для 400 записей. Средняя относительная погрешность составляет 2,67% при максимальной относительной погрешности 64%. Коэффициент корреляции 0,99

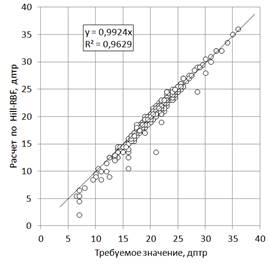
Рис. 5. Значения оптической силы ИОЛ, рассчитанные по формуле Hill-RBF для 400 записей. Средняя относительная погрешность составляет 2,75% при максимальной относительной погрешности 71%. Коэффициент корреляции 0,99

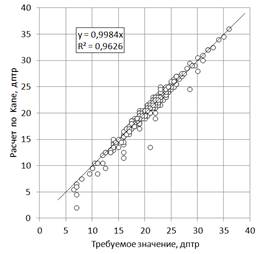
Рис. 6. Значения оптической силы ИОЛ, рассчитанные по формуле Kane для 400 записей. Средняя относительная погрешность составляет 2,78% при максимальной относительной погрешности 71%. Коэффициент корреляции 0,99

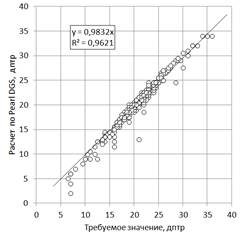
Рис. 7. Значения оптической силы ИОЛ, рассчитанные по формуле Pearl DGS для 400 записей. Средняя относительная погрешность составляет 3,21% при максимальной относительной погрешности 71%. Коэффициент корреляции 0,99

Таблица 1

Сравнение результатов предоперационных расчетов оптической силы ИОЛ для формул различных поколений на локальных данных

* Получено по аппроксимационой зависимости (рис. 2)

А – константа, модель ИОЛ; ACD – глубина передней камеры, мм; AL – длина глаза, мм; K – среднее значение кератометрии, дптр; K1 – рефракция слабого меридиана, дптр; K2 – рефракция сильного меридиана, дптр; LT – толщина линзы, мм.

Заключение

Таким образом, в данной статье на основе значительных выборок локальных эмпирических данных проведено сравнение уровня погрешностей расчетов оптической силы ИОЛ с помощью наиболее популярных формул второго, третьего и четвертого поколений. Показано, что современные формулы четвертого поколения по величине средней относительной погрешности в три-четыре раза превосходят пока еще используемые в офтальмологической практике формулы второго и третьего поколений. Процент попадания расчетных значений в диапазон ±0,5 дптр может приближаться к 68%, что несколько ниже, чем результаты, описанные в современной офтальмологической периодике.