Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Как никогда актуальны в настоящее время вопросы совершенствования системы подготовки инженерных кадров. На всех уровнях обсуждаются способы повышения мотивации к изучению естественно-научных предметов, звучат призывы обратить внимание на качество преподавания математики, физики и черчения.

Первый раздел всех графических дисциплин, среди которых «Инженерная графика», «Начертательная геометрия и компьютерная графика» и т.п., входящих в обязательный базовый модуль общепрофессиональных дисциплин высшего технического образования, составляет начертательная геометрия. Уже в первом семестре студенты машиностроительных направлений подготовки приступают к изучению инженерной графики, и начертательная геометрия – первая дисциплина, дающая студенту представление о выбранной специальности. Назревшая необходимость изменений в системе образования требует пересмотра и уточнения содержания дисциплины, насыщения программы более сложными и практико-направленными задачами. При этом важно уже на этапе разработки методики правильно определить место задач, верно сформулировать условия и требования, а также цели учебной деятельности.

Вопросам целеполагания в мировой и отечественной практике уделено достаточно много внимания. В современной российской педагогике высшей школы [1; 2] цели обучения тесно связаны с компетентностной парадигмой образования и определяются как планируемые результаты обучения, характеризующие полученные знания, умения и навыки, а также ряд других качеств, имеющих не только профессиональный характер, но транспрофессиональный: интеллектуальные, социальные и личностные [3]. Отмечается ориентация на индивидуализацию учебной деятельности, «усиление ответственности обучающихся за проектирование содержания своего обучения, определение персонализированных траекторий обучения» [4]. Обращается внимание на отличие целей научной деятельности от целей учебной дисциплины, где знания представляются в систематизированной и дидактически обработанной форме и ставятся цели не только передачи знаний, но и «развития учебно-профессионального интеллекта, гуманистического воспитания личности» [5]. Выявляются особенности компетентностного подхода, согласно которому просто обладать знаниями выпускнику вуза сегодня недостаточно, он должен уметь применять знания в профессиональной деятельности и в жизни. Поэтому цели обучения в вузе теперь формулируются как некий набор компетенций, под которыми подразумевается «совокупность знаний, умений и навыков, способностей и ценностей, необходимых для эффективной профессиональной деятельности и личностного развития выпускников, и которые они обязаны освоить и продемонстрировать после завершения части или всей образовательной программы» [6]. Контроль результатов обучения должен быть обеспечен определенным действием, связанным с целью обучения. Цель может быть не одна, и тогда строят так называемую таксономию – т.е. систему целей с разделением на уровни (этапы).

Наибольшую известность получила таксономия Б.Блума – многоуровневая классификация целей, разработанная Б.Блумом в 1956г. и усовершенствованная Л.Андерсоном и Д.Кратволем в 2001г. [7]. В последнее время она все чаще вызывает интерес у педагогов самых разных дисциплин [8]. Необходимость особого внимания к вопросам целеполагания учебной деятельности в новых условиях определила цель данного исследования – формирование таксономии целей при решении практико-направленных задач начертательной геометрии, образующих обучающий методический комплекс с системой контроля достижения запланированных результатов обучения.

Материал и методы исследования

В уточненной таксономии Блума познавательной деятельности шесть уровней (категорий): знание, понимание, использование, анализ, оценка и создание. Поскольку знания и навыки, полученные на некотором уровне, являются основой для изучения следующего, таксономию чаще всего изображают в виде пирамиды, уровни (категории) которой характеризуют результаты обучения [9]. Каждая категория определяет некоторые мыслительные действия–когнитивные процессы, соотносящиеся с навыками, которые должны быть сформированы у обучающихся в результате обучения [10]. Для описания целей и результатов обучения используются глаголы действия (табл. 1).

Таблица 1

Ключевые глаголы действия и вопросы для использования при разработке методического обеспечения дисциплины «Инженерная графика»

Составлено по [7].

Таксономия Блума может быть построена как для всего курса, так и для отдельного раздела, темы, занятия или задачи. Оценка результатов обучения по каждой категории производится на основе формулировок ее целей, а по уровню сформированности запланированных навыков можно оценить эффективность учебного процесса [11].

Конструирование целей проводят по этапам: сначала выделяют цели курса, затем цели текущей, повседневной деятельности. Описываемая работа выполнена с опорой на данные рабочей программы дисциплины (РПД) «Инженерная графика» для укрупнённой группы специальностей и направлений (УГСН) «Машиностроение» Санкт‑Петербургского политехнического университета Петра Великого (СПбПУ):

1. Цели освоения дисциплины: развитие образного, пространственного мышления, способностей к анализу и синтезу геометрических форм, овладение методами построения плоских проекционных моделей трехмерного пространства, формирование умений выражать свойства пространственных объектов и отношений между ними средствами геометрической модели, приобретение первоначального опыта проектирования машиностроительных объектов и выполнения конструкторских документов на основе стандартов ЕСКД, формирование навыков применения элементов инженерной компьютерной графики при разработке конструкторской документации.

2. Компетенции: способен работать с нормативно-технической документацией, связанной с профессиональной деятельностью, с учетом стандартов, норм и правил.

3. Индикаторы достижения компетенции: понимает конструкцию технического объекта по чертежу, демонстрирует первичные навыки выполнения конструкторских документов на основе стандартов ЕСКД.

4. Трудоемкость освоения первого раздела дисциплины (начертательной геометрии), составляет 2 з.ед. (зачетные единицы), лекции не предусмотрены, на практические занятия выделено 30 ак.ч. (академических часов), продолжительность курса – один семестр.

С использованием таксономии Блума выполнен анализ РПД дисциплины.

Результаты исследования и их обсуждение

Анализ целей и достигаемых компетенций показывает, что начертательная геометрия, несмотря на то что возможности применения ее методов гораздо шире, рассматривается только как дисциплина, формирующая базовые знания для дальнейшего освоения сначала следующего раздела курса – непосредственно инженерной графики, и далее общетехнических и специальных дисциплин, таких как «Детали машин», «Технология конструкционных материалов» и ряда других. Более точная формулировка целей изучения начертательной геометрии и результатов обучения, разработанная по таксономии Блума, приведена в таблице2.

Таблица 2

Обобщенные цели и результаты изучения дисциплины «Начертательная геометрия»

Достижению обозначенных целей и пониманию студентами предназначения дисциплины, азначит, и заинтересованности студентов в освоении науки, способствует решение практико-направленных задач. Рассмотрим пример задачи и покажем, как использование таксономии Блума может помочь преподавателю спланировать занятие, добиться усвоения нового материала обучающимися с максимальной эффективностью. Рисунки 1и2 отражают содержание задачи: по данному наглядному изображению детали необходимо построить три основных вида, выполнить необходимые разрезы и сечения, оформить чертеж.

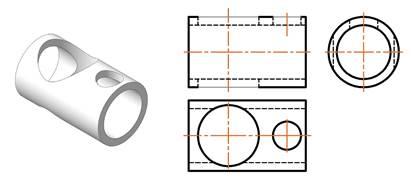
Рис.1. Пример задачи. Наглядное изображение фигуры и ортогональные проекции ее поверхностей

Сначала студенты строят контуры изображений: очерковые образующие цилиндров и вырожденных проекций их поверхностей (рис.1), без проекций линий пересечения поверхностей. При объяснении темы (первом решении задачи подобного рода) заготовка чертежа выдается. Следующие этапы решения показаны на рисунке 2.

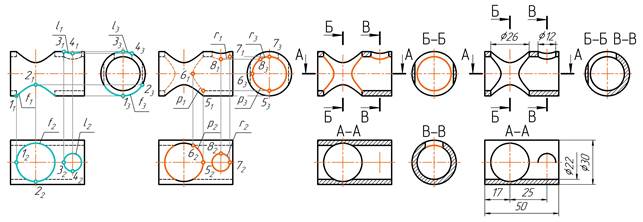
Рис. 2. Этапы решения практико-направленной задачи: а – построение проекций линий пересечения наружных поверхностей, б – построение проекций линий пересечения внутренних поверхностей, в – построение разрезов и сечений, г – нанесение размеров

Для формирования навыков распознавания форм и анализа характера линий пересечения поверхностей и их проекций разработан комплекс моделей и наглядных изображений, примеры которых представлены на рисунке3.

Рис. 3. Примеры заданий для тренировки навыков анализа формы деталей машин

Практическое значение задач очевидно: фигуры имеют форму и содержат элементы деталей машин. Рассматриваемая в примере пара пересекающихся цилиндрических поверхностей вращения с взаимно перпендикулярными пересекающимися осями – наиболее часто встречающая в инженерной практике.

Задачи предлагаются студентам на завершающем этапе изучения дисциплины, поэтому цели, которые ставит перед студентами преподаватель в процессе обучения алгоритму решения подобных задач, и достигаемые результаты перекликаются с указанными в таблице2. Таблица 3 отражает структуру занятия, составленную с помощью ключевых глаголов таксономии Блума и возможных вопросов, отобранных специально для использования в методических разработках по дисциплине «Инженерная графика» (табл.1).

Таблица 3

Структура занятия по теме «Построение линий пересечения поверхностей деталей машин»

Согласно сформированной методике, объяснение темы проводится с использованием разноуровневых вспомогательных заданий и вопросов. Каждый уровень, по Блуму, описывает возможные результаты обучения студента на соответствующем этапе, и переход на следующий, более сложный уровень возможен только после усвоения учебного материала предыдущего. Глаголы трех низших категорий соответствуют репродуктивному уровню познавательной деятельности, на более высоких уровнях – продуктивному, включающему более сложные навыки мышления. Поэтому для большинства этапов решения задачи практического характера задействованы только уровни знания (запоминания), понимания и применения. Глаголы действия, используемые в методике Блума для описания целей, применяют также и при разработке материалов для текущего и промежуточного контроля. Для оценки результатов обучения на уровне запоминания обычно используют тесты, для более высоких уровней необходимы другие методы.

В таблицу 3 внесены только этапы построения линий пересечения поверхностей. Порядок формирования разрезов и сечений, правила их оформления, нанесения размеров и оформления чертежа детали (рис.2 в, г) в соответствии со стандартами Единой системы конструкторской документации (ЕСКД) рассматриваются на занятии, но эта тема требует отдельного внимания, уделить которое в рамках данной статьи возможности нет.

Автором отмечено положительное влияние использования таксономии на качество проведения занятия. Структурирование помогает организовать учебную деятельность. Однако следует обращать внимание преподавателей на недопустимость формального подхода, вредность чрезмерного усердия в следовании правилу, запрещающему переход на более сложный уровень до полного усвоения учебного материала предыдущего. Это было и остается основной причиной критики таксономии Блума, поскольку может ослабить заинтересованность и мотивацию к учебе у студентов, тормозить развитие одаренных обучающихся, а также интерес к учебному процессу у самого преподавателя.

В завершение обсуждения обратим внимание: несмотря на развитие компьютерной техники, методов 3D-моделирования и инструментов формирования конструкторской документации с помощью построенных моделей, решение задач, подобных рассмотренной встатье, с выполнением построений на бумаге карандашом, по мнению авторов, остается совершенно незаменимым упражнением, формирующим и развивающим логическое мышление, навыки анализа формы технических объектов, без чего невозможен процесс компьютерного моделирования, анализа изображения на чертеже и выявления ошибок, что является необходимым условием осуществления проверки правильности модели. Знание закономерностей отображения линий пересечения на чертеже и умение «видеть» эту задачу при чтении и разработке чертежа детали – одна из важнейших инженерных компетенций, признак успешно пройденного первого этапа формирования инженерного мышления.

Заключение

В современных условиях преподавания, когда количество отведенных на дисциплину часов продолжает сокращаться, а число студентов в группах увеличиваться, особенно остро стоит вопрос рационального построения учебного процесса.

В рассмотренной работе авторами рассмотрен порядок формирования целей и методы контроля усвоения учебного материала с опорой на таксономию Блума при выполнении заданий графических дисциплин «Инженерная графика», «Инженерная геометрия и компьютерная графика», «Начертательная геометрия». Пример разработанной методики проведения занятия, посвященного разбору алгоритма решения задачи начертательной геометрии с ярко выраженным практическим значением, демонстрирует, что таксономия может с успехом применяться как для всего курса, так и для отдельных разделов и задач. Показано, что грамотно, с точки зрения методологии преподавания, сформулированные цели помогают преподавателю определить содержание учебного материала, выбрать объем и содержание заданий, методов преподавания, оценить результаты обучения, построить занятие в соответствии с индивидуальными особенностями студентов в разных группах, с учетом мотивированности и уровнем подготовленности, развивая мотивацию и интерес к дисциплине.

Периодическая критика таксономии Блума, связанная в основном с излишней формализацией, не мешает последователям Блума развивать и применять его теорию. Так, например, в настоящее время благодаря системности подхода таксономию Блума активно используют при разработке электронных учебников. Авторы видят возможность использования описанной в статье методики как основы для разработки электронной версии тренажера по решению задач, пример которой рассмотрен в статье.

Обобщая опыт, авторы делают вывод: таксономия Блума дает возможность осуществления системного подхода к разработке всех этапов и уровней учебного процесса. Это улучшает качество учебного процесса, повышает заинтересованность студентов визучении предмета, а преподавателей – в совершенствовании педагогических навыков.