Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

В действующих программах значительно усилена прикладная направленность школьного курса математики. Наиболее существенным изменениям в этом отношении подверглись программы старших классов. Однако их успешная реализация во многом зависит от того, в какой мере обучающиеся основной школы овладеют приемами и методами решения простейших задач прикладной направленности, научатся выявлять необходимые для их решения связи между практикой и теорией. Реализуются эти связи в первую очередь с помощью языка. Исторически сложилось так, что жители целого ряда удаленных районов Республики Тыва общаются между собой на родном тувинском языке. Это означает, что для многих взрослых жителей республики и их детей языком практики и жизни является тувинский язык. С другой стороны, теоретические положения и научные концепции формируются в вузах и научных центрах. В условиях России это означает, что языком теории и науки является преимущественно русский язык. Следовательно, для выявления необходимых для решения прикладных задач связей между практикой и теорией в республике желательно хорошо владеть как тувинским, так и русским языком. Это означает, что проблема успешного обучения тувинских школьников решению задач прикладного характера имеет не только содержательно-математический аспект, но и языковой.

Для решения содержательно-математического аспекта проблемы авторами предлагается пополнить традиционную методику решения прикладных задач анимационным подходом. Основные положения концепции обучения математике с использованием компьютерной анимации разработаны В.В. Абдулкиным, С.И. Калачевой, М.А. Кейв, С.В. Лариным и В.Р. Майером в монографии [1, с. 37], где под компьютерной анимацией понимается «компьютерная имитация реального или идеального процесса с помощью изменения формы объектов, текста или показа последовательных изображений с фазами движения» [1, с. 8]. Методика применения компьютерной анимации была успешно апробирована С.В. Лариным и В.Р. Майером в гимназиях № 13 и 14 г. Красноярска с использованием учебного пособия [2, с. 25] и на математических курсах Красноярского государственного педагогического университета им. В.П. Астафьева [3, c. 228]. Реализовать анимационный подход можно на базе любой системы динамической математики. Однако, по мнению авторов, наибольшие анимационные возможности заложены разработчиками в среду «Живая математика» [4, с. 102]. Именно они успешно применялись при решении задач прикладного характера в [5]. Отметим здесь, что под задачами прикладного характера будем понимать задачи, поставленные вне математики и решаемые математическими средствами. Прикладные задачи являются одним из основных средств ознакомления с приложениями математики, которые являются неотъемлемой частью математического образования. Это один из важнейших видов задач, формирующих образовательные, воспитательные и развивающие навыки в математическом образовании.

Для преодоления трудностей, связанных с языковым аспектом проблемы, предлагается взять на вооружение билингвальный подход. Существует несколько достаточно близких по содержанию определений понятия билингвизма. В данной работе, как и в статье [6], под билингвизмом будем понимать двуязычие, которое рассматривается как равноправное существование двух языков в пределах одного этноса, владение человеком двумя языками и практика их попеременного пользования, умения с их помощью осуществлять успешную коммуникацию либо одинаковое владение двумя языками. В республике различают несколько видов билингвизма, например русско-тувинский, тувинско-русский, кыргызско-русский, кыргызско-тувинский. В данной статье авторы рассматривают в основном тувинско-русский билингвизм. Теорией обучения математике в условиях этого двуязычия занимались такие исследователи, как Ю.В. Вайнштейн, С.К. Саая, Н.М. Кара-Сал, А.С. Монгуш, К.В. Сафонов, О.М. Танова, М.В. Танзы, В.А. Шершнева и другие [7–9].

Условимся в дальнейшем подход к обучению с использованием возможностей билингвизма и компьютерной анимации именовать термином «билингвально-анимационный подход», сокращенно «БЛА подход». Ключевая идея этого подхода применительно к обозначенной выше проблеме заключается в том, что при решении прикладной задачи предлагается максимально использовать возможности компьютерной анимации, при этом формулировку задачи и комментарии по ее решению сопровождать как на тувинском, так и на русском языках.

Цель статьи – продемонстрировать возможности использования билингвально-анимационного подхода в обучении решению прикладных задач на уроках математики в основной школе в условиях тувинско-русского двуязычия.

Материалы и методы исследования

Методологическую основу работы составили системно-деятельностный, личностно-ориентированный и когнитивно-визуальный подходы. Анализ, обобщение и систематизация научно-методической литературы, исследований отечественных и зарубежных авторов по проблеме обучения решению задач прикладной направленности на уроках математики в основной школе с использованием билингвального подхода и компьютерной анимации. Значимое место среди методов исследований в работе заняли элементы опытной работы.

Важнейшим классическим методом решения прикладных задач является математическое моделирование. Одним из средств математического моделирования реальных зависимостей служат эмпирические графики. Их применение опирается на приобретенные в 5 классе навыки работы обучающихся с диаграммами. Обучение решению прикладных задач с использованием эмпирических графиков проходит успешнее в том случае, если учащимся ясна цель их введения, если функциональный аппарат применяется ими для решения задач прикладного содержания, использующих личный опыт учащихся, их живой интерес к явлениям тувинской природы, склонность к наблюдениям. В качестве примера использования БЛА подхода рассмотрим следующую задачу, которую можно предложить обучающимся на уроке математики в 6 классе.

З а д а ч а 1. На анимационном чертеже среды «Живая математика», представленном двумя стоп-кадрами на рис. 1, изображен график изменения температуры воздуха в течение суток. С ним связаны два отрезка: ОА, изображающий время в часах, прошедшее от начала суток, и АВ, изображающий температуру воздуха в градусах. Представьте, что отрезок ОА увеличивается и его правый конец, точка А, проходит последовательно точки, отмеченные числами 2, 4, …, 24. Вместе с этим меняется и длина отрезка АВ. Пользуясь графиком, ответьте на следующие вопросы:

1) В какие часы суток температура возрастает, в какие – убывает? Какая температура была в 10 часов? В 20 часов?

2) Какого наименьшего (наибольшего) значения в эти сутки достигла температура и в каком часу это произошло?

Для реализации анимационной составляющей БЛА подхода в среде «Живая математика» создается динамический чертеж. Разработка такого чертежа по заранее подготовленной таблице с температурными значениями не представляет большого труда. Кстати, к сбору необходимых табличных данных можно привлечь обучающихся.

Рис. 1. Стоп-кадры компьютерной анимации, поддерживающей решение задачи 1

После обращения к команде «Построить график по данным из таблицы…» на экране появится изображение координатной сетки и требуемый эмпирический график. Далее остается поместить на ось времени произвольную точку А, найти соответствующую ей точку В на графике, изобразить отрезки ОА и АВ.

Для удобства обучающихся и большей наглядности на чертеже с помощью заранее подготовленных собственных инструментов изображаются часы и градусник. Особенность инструмента «Часы» заключается в полной синхронности длины отрезка ОА и соответствующих положений часовой и минутной стрелок. Для создания этого инструмента необходимо знание некоторых свойств окружности, поэтому к участию в его разработке можно привлечь обучающихся 8 или 9 классов. Особенность инструмента «Градусник» заключается в полной синхронности отрезка АВ и высоты ртутного столба в градуснике. Справиться с его разработкой под руководством учителя могут обучающиеся 6 класса.

Задать анимацию можно несколькими способами, отметим два из них, которые в соответствии с классификацией из [1, с. 16] называются «кнопочной» и «ручной» анимациями. В первом случае подсвечивается точка А, затем в меню «Правка» выбирается опция «Кнопки», далее – команда «Анимация». На экране появляется кнопка, после нажатия на которую начинает перемещаться А, вслед за ней приходят в движение стрелки часов, меняются показания градусника. Более полезной для исследования является ручная анимация. Для ее реализации достаточно подсветить точку А и перемещать ее, используя для этого компьютерную мышь или клавиши управления курсором.

Для реализации билингвальной составляющей БЛА подхода в верхней части экрана создаются две кнопки (рис. 1), одна из которых выводит на экран формулировку и комментарии к решению задачи на русском языке, вторая – на тувинском языке.

Как известно, большие прикладные возможности заложены в графиках движения, поэтому в качестве примера использования на уроках алгебры компьютерной анимации приведем следующую задачу, которую можно с успехом рассмотреть в 7 классе при изучении линейных зависимостей.

З а д а ч а 2. На анимационном чертеже, выполненном в среде «Живая математика» и представленном двумя стоп-кадрами на рис. 2, изображены графики движения пешеходов, идущих по одной дороге навстречу друг другу.

1) Опишите движение пешехода, идущего из Березовки в Сосновку:

а) В какое время вышел пешеход из Березовки в Сосновку? б) На каком расстоянии от Сосновки был он в 9 часов? в) В котором часу и на каком расстоянии от Сосновки отдыхал? г) С какой скоростью прошел первую половину пути, с какой – вторую? д) В котором часу прибыл он в Сосновку?

2) Опишите движение пешехода, идущего из Сосновки в Березовку:

а) В котором часу пешеход вышел из Сосновки? б) В котором часу пешеход пришел в Березовку? в) С какой скоростью прошел он весь путь? г) Делал ли он остановки в пути?

3) Сравните движения обоих пешеходов:

а) На каком расстоянии друг от друга были пешеходы в 11 часов? б) В котором часу и на каком расстоянии от Сосновки пешеходы встретились? в) В котором часу пешеходы были на расстоянии 5 км друг от друга в первый раз, во второй раз?

Для создания анимационного эффекта на горизонтальную ось времени t (рис. 2) помещена произвольная точка, которая обозначена t0. Перемещать ее можно вручную с помощью мыши. Через t0 проведена вертикальная прямая, точка пересечения этой прямой с графиком движения пешехода, идущего из Березовки, обозначена через Б, точка пересечения вертикальной прямой с графиком движения второго пешехода – через С.

Для того чтобы обучающиеся ни в этой задаче, ни в дальнейшем не путали графики движения объектов с их траекторией перемещения по трассе, желательно на первых порах при решении задач на движение помимо графиков приводить изображение трассы и движущихся по ней объектов. При этом траекторию трассы следует изображать существенно отличающейся по форме от графиков движения. В связи с этим чуть ниже координатной сетки изображен в виде отрезка фрагмент дороги, проходящей через Сосновку и Березовку, на дороге изображены фигурки обоих пешеходов. Пешеход, вышедший из Березовки, находится от Сосновки на расстоянии, равном длине отрезка, соединяющего точки t0 и Б, второй пешеход – на расстоянии, равном длине отрезка, соединяющего точки t0 и С. Кроме этого, для удобства обучающихся справа от графиков помещено изображение циферблата с минутной и часовой стрелками, положение которых также зависит от выбора точки t0.

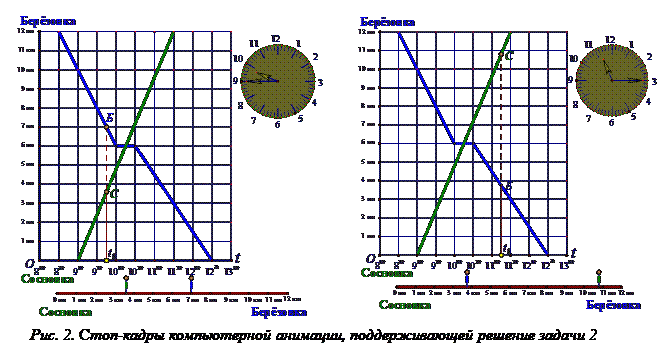
Таким образом, обучающиеся, меняя с помощью мыши положение точки t0, могут одновременно наблюдать соответствующие изменения как точек Б и С на графиках движения, так и фигур пешеходов на дороге. Кроме этого, они имеют возможность с достаточно большой точностью находить требуемые в соответствии с условием задачи значения времени и расстояния. Так, например, на левом слайде рис. 2 положение пешеходов соответствует значению времени 9 ч 45 мин, на правом слайде – 11 ч 15 мин. Причем в первом случае расстояние между пешеходами равно 3,40 км, во втором – 7,05 км.

Результаты исследования и их обсуждение

Всего в общей сложности авторами разработаны в среде «Живая математика» 48 анимационных чертежей, поддерживающих систему задач прикладного характера, главное назначение которой – исподволь, начиная с 6 класса, готовить учащихся к неформальному усвоению основных понятий и методов математического анализа в школах Республики Тыва. Несколько пробных уроков с использованием билингвально-анимационного подхода проведено авторами в 7 и 8 классах школы № 1 им. М.А. Бухтуева, и также в 7 и 8 классах школы № 3 им. героя Советского Союза Т.Б. Кечил-оола г. Кызыла. В общей сложности на занятиях присутствовало 106 учеников, в каждом классе на четырех уроках удалось решить по восемь прикладных задач. Опрос, проведенный среди этих обучающихся, позволяет сделать вывод о большом эмоциональном эффекте, который оказывает анимационное сопровождение обсуждаемых задач на учебную атмосферу в классе во время таких уроков. В большинстве случаев динамические чертежи позволяют максимально визуализировать сюжет прикладной задачи, что в соответствии с основным дидактическим принципом наглядности способствует успешному ее решению. Отметим также, что прикладная задача, сформулированная не только на русском, но и на родном для обучающегося тувинском языке, дает наиболее глубокое осмысление ее условия. Помимо обучающего эффекта такое терминологическое сопровождение задач является эффективным средством успешного развития этнокультурной идентичности обучающихся, не владеющих родным языком, и наоборот.

Предложенный в статье авторский подход обучения решению задач прикладной направленности на уроках математики в основной школе Республики Тыва, в основе которого лежит интеграция билингвального и анимационного подходов, позволяет мотивировать обучающихся на заинтересованное решение обсуждаемых задач, создает эффект успешности участия каждого ученика в совместном обсуждении способов решения задач, способствует формированию у обучающихся исследовательских умений и навыков.

Заключение

Обучение решению задач прикладной направленности в 7 и 8 классах с применением анимационных чертежей, сопровождаемых поддержкой на тувинском языке, положительно воспринимается обучающимися. Анимационные чертежи, создаваемые в среде «Живая математика», пополняют арсенал традиционных средств обучения математике в условиях двуязычия. Ясно, что применение этого подхода целесообразно лишь на первых порах решения прикладных задач каждого типа. Чрезмерное увлечение таким подходом может негативно сказаться как на развитии логического мышления, так и на формировании пространственного воображения и геометрической интуиции обучающихся.

Отметим, что предложенный авторами подход имеет практическую значимость, его легко адаптировать к обучению решения прикладных задач в условиях любого двуязычия.