Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

В последнее время в обществе произошел разрыв между потребностями науки и техники и существующим уровнем математической культуры будущих инженеров, что объясняет актуальность выбора темы данного исследования. Терминология математики и методы математического мышления пронизывают практически все области науки и техники. Подготовка современного инженера невозможна без интеграции в профессиональную культуру математической, которая обеспечивает общий, понятный для всех наук и профессий язык общения, прививает умение логически мыслить, обобщать, анализировать, делать выводы, применять методы индукции и дедукции, развивает прогностическую функцию мышления. Математическое мышление обеспечивает возможность воспитания инженеров, отвечающих потребностям общества, способных к мобильности в профессиональной сфере, совершенствованию и инновациям.

Цель исследования – создать благоприятные условия формирования математической культуры студентов в рамках учебно-воспитательного процесса в КНИТУ при обучении студентов технологических направлений.

Материал и методы исследования

В качестве объекта исследования рассматривается процесс формирования элементов математической культуры студентов Инженерного химико-технологического института КНИТУ.

Предмет исследования – формирование элементов математической культуры при обучении студентов Инженерного химико-технологического института КНИТУ первого и второго курсов с применением авторского курса.

Изменения в содержании и характере профессиональной деятельности инженера-технолога определяют изменение требований к его математической культуре, что влияет и на наполнение курса математики. В качестве задачи исследования авторы выбрали задачу создания авторского курса высшей математики для технологических направлений обучения, углубив изучение наиболее важных в профессиональном смысле математических понятий и навыков и дополнив содержание курса разноуровневыми профессионально значимыми задачами. Новизна исследования определяется изменениями требований к математическим компетенциям инженера, необходимостью согласовать курс математики с применением математического аппарата в специальной подготовке, а также тем, что решение такой важной проблемы как формирование устойчивых элементов математической культуры, происходит при значительном сокращении количества аудиторных часов, выделяемых на изучение предмета.

Результаты исследования и их обсуждение

Требование времени ставит перед высшим образованием задачу подготовки специалистов, обладающих практическим и научным потенциалом, способных активно развивать нашу науку, промышленность и экономику. Во многом результативность работы инженера определяется сформированностью его научного фундамента. Взаимопроникновение наук, увеличение математической составляющей в их понятийном аппарате позволяет усилить прогностическую функцию научных знаний [1].

Большинство современных авторов, занимающихся исследованиями вопросов, связанных с математической культурой специалиста технического или технологического профиля, понимают под математической культурой систему знаний, умений, навыков и методов, полученную в процессе изучения математических дисциплин, а также естественнонаучных, общепрофессиональных и специальных дисциплин общего и профессионального образования.

Среди элементов математической культуры принято выделять:

- владение языком математики в различных формах - устной и письменной;

- сформированность логического мышления, развитость пространственного воображения;

- владение абстрактным математическим аппаратом;

- представление о возможности применения математических понятий в технических и технологических задачах;

- сформированность критического мышления;

- способность к саморазвитию;

- использование истории развития математики для развития культуры личности.

Процесс формирования элементов математической культуры начинается в школе, продолжается в высших учебных заведениях и на всех этапах профессиональной деятельности инженера [2]. Управление процессом формирования математической культуры в вузе осуществляется на основе научного планирования, организации и контроля. Важнейшие базовые компоненты математической культуры — развитое математическое мышление и язык. Совокупность средств обозначения, изложения и записи математических суждений и идей (терминология, символика, письменная и устная речь) составляют язык математики. Как и другие, язык математики имеет свой словарь символов и слов, свою грамматику. Система обозначений математики ассимилировала символы из других алфавитов, например греческий, латинский, а также имеет и специальные математические знаки. В словарь математики входят и визуальные элементы, например диаграммы. Грамматика математики включает в себя правила написания и чтения формул. Разработаны типографские соглашения при печатном изложении математических текстов. Уровень владения математическим языком и развитость логического абстрактного мышления и пространственного воображения взаимозависимы. Свойства математического мышления — это ясность, точность, лаконичность выводов, изложения материала текста или беседы, самостоятельность мышления, аргументированность, критичность, доказательность суждений. Математическое мышление – это теоретическое мышление, объекты которого могут быть наполнены разным содержанием. Сформированность математической культуры предполагает умение грамотно и лаконично строить математические формулировки как устно, так и письменно с использованием математической символики. Умение формулировать и понимать математические фразы (каждая из которых несет определенную математическую мысль) наиболее эффективно развивается во взаимодействии с носителем математической культуры, при работе с математическими текстами, при постановке, решении и обсуждении задач и полученных результатов.

Проводя из года в год входное тестирование студентов, поступивших на первый курс КНИТУ, авторы отметили недостаточный уровень сформированности их математической культуры, что проявляется, в основном, в неумении читать, формулировать и анализировать математические тексты. Причем дидактическая литература для развития математического языка практически отсутствует. Для адаптации студентов к обучению в вузе, усвоения нового теоретического материала курса, а также для восполнения существующего пробела математической культуры авторы использовали в разработанном курсе задания различных типов:

– задания, имеющие цель закрепить знание основной символики языка, его терминологии и основных понятий (тесты, содержащие верные и неверные математические предложения, где требовалось выбрать правильные утверждения или дополнить утверждения). Пример подобного задания:

- Являются ли коллинеарные вектора компланарными?

1) не являются; 2) да, но при определенных условиях; 3) являются при любых условиях.

– задания, позволяющие отрабатывать владение терминологическим аппаратом на более высоком языковом и понятийном уровнях с использованием логических связи (например, задания, выполнение которых требует знание определений, свойств математических объектов). Например:

- Если векторы коллинеарны, то модуль их скалярного произведения равен:
1) произведению длин данных векторов; 2) нулю; 3) сумме длин данных векторов.

– задания, развивающие критическое мышление и индивидуальные творческие способности студентов (задания, где требуется поиск или выбор оптимального решения, соответствующего заданным исходным данным). Например: определить линейно независимые реакции процесса получения СО2 при взаимодействии водяного пара с углем:

H2O + C = CO + H2

H2O + CO = H2 + CO2

2CO = CO2 + C

2H2O + C = 2H2 + CO2

Математическая культура инженера включает в себя две взаимосвязанные компоненты: информационную и деятельную. При формировании информационной компоненты используется опыт человечества, индивидуальный опыт преподавателя (носителя математической культуры) и самого студента. В условиях крайне ограниченного аудиторного времени выделенного на изучение курса высшей математики в вузе и огромного объема знаний, накопленного человечеством, роль преподавателя в этом процессе является определяющей. В основе содержания информационной компоненты математической культуры инженера должен лежать принцип баланса между фундаментальной и профессиональной направленностью курса высшей математики [3].

На начальном этапе формирования элементов математической культуры в вузе главным педагогическим условием является формирование мотивации к обучению. Студенты младших курсов не обладают специальными знаниями и не могут оценить значимость математических методов в дальнейшей их деятельности. С целью популяризации математических идей и методов классический лекционный курс авторы дополнили материалом, содержащим истории и причины возникновения математических понятий и их развитие. Заинтересованность к изучению материала курса высшей математики усиливается показом связи изучаемых абстрактных понятий с физическими, их геометрического смысла, а математические утверждения сопровождаются примерами и контрпримерами.

Формирование профессиональной культуры будущего инженера в вузе происходит на протяжении всего учебно-воспитательного процесса [4]. Интегрирование математической культуры в профессиональную связано с профессиональным ориентированием содержания математического образования. Проведенный обзор и анализ требований, выдвигаемых к уровню профессиональной подготовки выпускников технологических направлений, показал, что наиболее значимыми разделами курса высшей математики оказались линейная алгебра; теория множеств; элементы топологии; дифференциальное и интегральное исчисление, математическая статистика. Для усиления мотивации к обучению и выработки единой системы обозначений, авторами эти разделы были дополнены задачами прикладного характера. Например, в разделе «Линейная алгебра» рассматривалось решение задач расчета смесей сложного состава [5]. В таких задачах нужно определить количество каждой из компонент, необходимых для приготовления смеси. Например, требуется приготовить смесь из m веществ. Смесь должна содержать 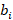единиц i - го вещества (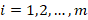) и для ее приготовления есть n компонентов, каждый из которых (j -ый) содержит 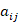единиц i-го вещества (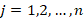). Если 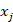количество j-го компонента, которое необходимо взять для приготовления смеси, то математическая модель задачи можно записать в виде системы линейных алгебраических уравнений:

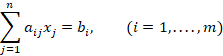
Приведем задачу с конкретными данными. Требуется приготовить 4250 кг нитрующей смеси из трех компонент: 22% воды (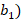, 16% азотной кислоты (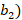, 62% серной кислоты (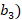из смеси: 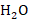– 5% (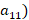, 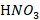– 85% (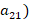, 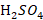-10% (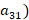; из олеума: : 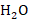– 0% (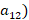, 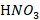– 0% (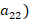, 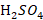-104% (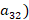; из отработанной кислоты : 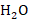– 30% (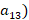, 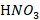– 0% (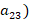, 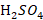-70% (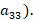Нужно найти расход кислот, идущих на приготовление этой смеси. Записав математическую модель задачи в виде системы линейных алгебраических уравнений, можно легко найти ее решение.

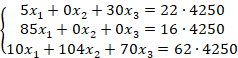
Применив, например методом Крамера, получим .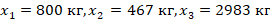

Возникновение наукоемких технологий диктует новые требования к профессиональным компетенциям инженера. Преподавателями нашей кафедры были проведены беседы и опросы преподавателей выпускающих кафедр КНИТУ, готовящих инженеров-технологов. На основе собранного материала были проведены анализ, и систематизация наиболее часто встречающихся профессионально ориентированных задач и выделены значимые понятия математики, используемые при их решении. Например, при решении задач расчетов смесей сложного состава, определения состава смеси по данным спектрофотометрических измерений, при проведении исследования состава смеси с помощью системы химических сенсоров, при анализе размерностей величин, широко применимы такие математические понятия раздела линейной алгебры, как система линейных алгебраических уравнений, ее решение, матрица, ранг матрицы, определитель, метод Гаусса, правило Крамера. При решении таких задач, как построение линии равновесия состава, нахождение максимальной скорости окисления, определение максимального выхода продукта, исследование автокаталитических реакций, применяются понятия математического анализа такие как, пределы, производная и ее приложения, выпуклость, вогнутость функции, экстремум, асимптоты графика функции.

Для эффективного управления процессом формирования математической культуры и установления баланса между фундаментальной и профессиональной составляющей содержания, авторы провели корректировку содержания курса высшей математики, и разработали комплекс профессионально ориентированных дифференцированных задач и заданий для студентов технологических направлений, представленных в КНИТУ.

Решение таких задач создает условия для приобретения навыков определения проблемных ситуаций, их научного анализа, построения математических моделей, исследования и нахождения их решений, то есть способствует формированию деятельной компоненты математической культуры в условиях вуза [6]. Для формирования способности к саморазвитию в курсе предложены индивидуальные расчетные задания, самостоятельно выполняемые студентами, с возможностью использования любой литературы и консультирования с преподавателем. С целью создания благоприятных условий формирования устойчивых элементов математической культуры в условиях ограниченного количества аудиторных часов, авторы использовали технологию смешанного обучения [7]. Часть занятий было перемещено в электронную среду, что позволило выделить время на решение профессионально-значимых задач. Соотношение аудиторной и виртуальной компонент в обучении зависело как от изучаемого материала, так и от уровня подготовки и мотивации обучаемых.

Высшая математика изучается в КНИТУ бакалаврами в течение трех, специалистами – четырех семестров. В каждом из семестров проводилось тестирование студентов экспериментальных групп для оценки уровня сформированности элементов математической культуры. В тестах использовались задания открытого и закрытого типа. При диагностировании уровня сформированности математической культуры авторы оценивали знание математической символики, основных понятий и свойств математических объектов, умение довести решение задачи до конца, представление результатов в стандартном виде. Результаты тестирования показали положительную динамику формирования элементов математической культуры. По окончании третьего курса опрос студентов экспериментальных групп (через год после завершения курса высшей математики), имеющих средний балл 4 по математике (за 4 семестра) показал, что большинство из них помнят основные понятия и знают терминологию, могут решать математические задачи с использованием справочных материалов. Преподавателями специальных дисциплин было замечено, что эти студентам меньше испытывают трудности при изучении материала.

Заключение

Для студентов технологических направлений обучения, представленных в КНИТУ (КХТИ), был разработан разноуровневый комплекс заданий, связывающих математические понятия с профессиональными задачами. Оценка сформированности математической культуры - это прежде всего качественная характеристика, отражающая уровень владения языком математики, умение логически мыслить, обобщать, анализировать, делать выводы, использовать методы индукции и дедукции, способности к самосовершенствованию. Наиболее активно формируются элементы культуры при личном общении с носителями культуры. Использование цифровых технологий в обучении позволили авторам обеспечить как фундаментальную, так и профессиональную направленностью курса. Внедрение авторского курса повысило уровень мотивации студентов к обучению, позволило сформировать необходимые элементы математической культуры. Положительные результаты работы по развитию математической культуры могут найти применение в методической работе вуза.