Включение элементов стохастики в федеральный стандарт общего образования востребовало тщательного понимания особенностей обучения соответствующих частей точных дисциплин [1], анализа возможностей предметов естественно-научного цикла при необходимости использования стохастических методов. Требуется указать эффективный набор инструментов изучения стохастики; установить критерии развития стохастической компетентности. На сегодняшний день образование ориентировано на практику, поэтому показателем образовательной работы школы должен стать набор основных компетентностей. Следовательно, одним из основных приоритетных направлений обучения школьников элементам стохастики является их развитие и подготовка к жизни в реальных условиях непрерывно изменяющегося мира.
Цель исследования: выявить некоторые инструменты, способствующие развитию базовых навыков стохастической компетентности обучающихся в общеобразовательной школе.
Материал и методы исследования. Отбор соответствующей литературы: философской, психолого-педагогической, методической; новых стандартов образования. Методологическую основу исследования составили: фундаментальные работы в области педагогики, психологии; системно-деятельностный, компетентностный подходы; исследования в области изучения элементов теории вероятностей и математической статистики в общеобразовательной школе.
Результаты исследования и их обсуждение. Известно, что компетентность − уже состоявшаяся совокупность личностных качеств учащихся, а также необходимый минимальный опыт деятельности. Компетенции предлагаются учащимся для овладения, формирования у них определенных компетентностей [2]. Для исследования механизмов формирования стохастической компетентности важна связь стохастики и математики в целом. Здесь авторы используют уже устоявшийся в научных исследованиях термин «стохастическая компетентность», подразумевая, что это компетентность в области стохастики (объединяющей элементы теории вероятностей, комбинаторики, математической статистики и некоторых элементов теории множеств, теории графов, математической логики и др.) [2].
Под математической компетентностью вслед за Н.С. Седовой будем понимать «доказанную подготовленность к деятельности, которая показывает уровень владения базовыми математическими знаниями, умениями, навыками и способность их применять в конкретных и зачастую (выделено авторами) нестандартных ситуациях» [2]. В структуру математической компетентности включают следующие элементы: психологическую подготовку, позволяющую учащимся применять математические знания в образовательной деятельности; наличие уверенности в своих возможностях успешно привлекать математические методы и средства при решении задач; желание познавать новое и готовность выходить за рамки обычной деятельности.
В качестве основных структурных единиц математической компетентности выделяются мотивационно-ценностные, содержательно-процессуальные и рефлексивные элементы. В настоящее время происходит математизация науки, и в частности увеличение роли стохастических методов во всех областях деятельности человека. Для того чтобы современный человек считался образованным, он обязан иметь представления о коммуникации случайного и необходимого, о стохастических и динамических закономерностях, о возможностях принятия оптимальных решений. На сегодняшний день просматривается тенденция применения стохастики в качестве языка для исследования различными способами возникающих проблем в различных сферах деятельности. Наиболее острой является необходимость формирования стохастической культуры и, конечно же, стохастической компетентности учащихся [3]. Внедрение элементов стохастики в школьный курс в рамках новой учебной дисциплины «Вероятность и статистика», помимо систематической работы по формированию основных понятий и базовых навыков стохастической компетентности, требует также пропедевтической работы в начальной школе. Здесь основным средством развития стохастических представлений является статистическое наблюдение и представление добытой информации с использованием геометрических образов [4]. Следует отметить, что для многих учащихся наша система образования предоставляет уникальную и порой единственную возможность освоить базовые понятия и методы стохастики, приблизиться к стохастической культуре, овладеть ценностными знаниями в области стохастики. Под становлением стохастической культуры предполагается процесс учебной деятельности, направленный на «осознанное овладение стохастическими знаниями и умениями, также развитие познавательной мотивации, стохастического мышления, культуры исследовательской деятельности» [5, с. 118-119]. Как и любой вид компетентности, стохастическая компетентность включает в себя теоретическую (владение понятиями стохастики) и практическую (навыки владения методами стохастики) подготовленность обучающихся, а также способность применения знаний и умений в реальной ситуации. Кроме того, предполагается также мотивационная готовность (ученик не только может, но и хочет применять знания и умения). Стохастическая компетентность входит в состав математической компетентности, тем самым является компонентом базовой компетентности. Фиксируются следующие ключевые условия приобретения необходимой степени стохастической компетентности учащихся: знание элементарных основ стохастики; знание методов стохастического анализа реальной действительности; применение принципов стохастики в учебном процессе и в процессе жизнедеятельности; владение фундаментом стохастического мышления. Укажем на ряд компонентов стохастической компетентности и их роль в подготовке учащихся по вероятностно-статистической линии: целевой, содержательно-математический, алгоритмический, прикладной, вероятностно-прогностический, логико-вероятностный (показывает специфичность стохастических рассуждений), эвристический, имитационный (анализ связи между моделями аналогичной ситуации), межпредметный, внутрипредметный (фиксирует масштабность осмысления роли стохастики в математике), воспитательный компонент, организационно-деятельностный. Воплощение в жизнь перечисленных компонентов делает возможным обеспечить набор базовых навыков стохастической компетентности учащихся в области комбинаторики, статистики, теории вероятностей, а также развитие мышления.
Укажем на некоторые инструменты, способствующие развитию стохастической компетентности учащихся.
1. Интерактивные методы обучения. В научной литературе обращается внимание на эффективность интерактивных методов в обучении стохастике [6]. Сами по себе стохастические компетенции немыслимы без активности школьника и соответствующих этой активности методов обучения. Развитые стохастические компетенции предполагают выполнение следующих функций: поднимают познавательную мотивацию учащихся к изучению стохастического материала; учат приемам статистического анализа данных; совершенствуют навыки публичного обмена мнениями, выполнения самостоятельной работы; воспитывают навык к партнерскому общению; делают доходчивым для усвоения тяжелый теоретический материал вероятностно-статистической линии. При построении стохастической модели задачи интерактивными методами ученику приходится самому понять ее реальное содержание, представив конкретную жизненную либо профессиональную ситуацию, часто приходится провести исследование, эксперимент, поставить опыт. Поэтому при использовании интерактивных методов обучения необходимо организовать целеустремленное сотрудничество учителя и учащихся по решению учебных проблем во взаимодействии друг с другом, моделируя различные ситуации, оценивая совместные действия в атмосфере реального делового сотрудничества. Эти методы обеспечивают оптимальные условия для развития стохастической компетентности у школьников. Работа в команде невозможна без интеллектуальной активности каждого, при этом язык стохастики становится языком общения школьников, а достижение общей цели происходит благодаря не столько конкуренции, сколько кооперации совместных усилий. В интерактивной деятельности идея, мысль реализуются только при учете мнения каждого, сама деятельность организуется так, чтобы высказался каждый. Для этого класс обычно делится на группы, каждая из которых решает свою задачу, но общий результат зависит от усилий каждой группы.
Опираясь на основные структурные компоненты математической компетентности, можно выделить критерии для определения уровня развития стохастической компетентности: мотивационно-ценностный, содержательно-процессуальный, оценочно-рефлексивный. В связи с этими критериями могут быть сформированы диагностические задания. Заметим, что для основной школы при подборе заданий больше внимания необходимо уделять сформированности базовых навыков, но и применение более творческих заданий в неопределенных условиях также может присутствовать, их правильное выполнение позволит выявлять более высокий уровень овладения стохастической компетенцией. Интерактивные методы как раз способствуют решению стохастических задач в неопределенных условиях, когда решение не лежит на поверхности, не имеет готового алгоритма решения. И если в традиционном обучении в большей мере раскрывается содержательно-процессуальный компонент (знания и умения), то при компетентностно-ориентированном подходе на первый план выходят мотивационно-ценностный и оценочно-рефлексивный. В обычном обучении учитель – ведущий (объясняет, дает задания), ученик – ведомый (слушает, запоминает, решает по образцу). Здесь же учитель и ученик выступают в активной позиции. Учитель организует активную деятельность учеников, добивается самостоятельного решения задач. Такое обучение основывается на собственном опыте учащихся, их взаимодействии в области осваиваемого опыта. Причем формирование нового опыта реализуется с учетом наличествующего опыта, создания различных проблемных ситуаций на основе противоречий, возникающих в процессе решения задач, и образования других познавательных мотивов и интересов. Интерактивные методы обучения дифференцируют: выделяют игровые и неигровые ситуации в них. В частности, ко вторым из них относят использование компетентностно-ориентированных заданий. Остановимся подробнее на компетентностно-ориентированных заданиях, учитывая при этом специфику формирования стохастической компетентности.
2. Компетентностно-ориентированное задание (КОЗ) следует определять как объединенную дидактическую единицу содержания, технологии и мониторинга качества обучения [7]. Компетентностно-ориентированные задание охватывает практические основы, способствующие формированию знаний, умений, навыков и признание разумными тех качеств, которые содействуют выполнению самостоятельной познавательной деятельности [8; 9]. Суть формулирования и решения компетентностно-ориентированных задач: разведение стандартных и нестандартных ситуаций. КОЗ не направлены на простое транслирование информации и выполнение конкретных действий. Они способствуют организации учебно-познавательной, научно-исследовательской, межпредметной работы. К ключевым функциям компетентностно-ориентированных заданий общепринято причислять: получение новых знаний; углубление знаний; воспитательную; мотивационно-стимулирующую; управляющую; контрольно-оценочную. В типологии компетентностно-ориентированных заданий выделяют три основных типа: предметные, межпредметные, практические [9]. При реализации КОЗ учащиеся решают набор компетентностных задач, которые можно отнести к определенному виду из типологии. Чтобы школьникам гарантировать развитие необходимых компетентностей, следует к содержанию компетентностно-ориентированных заданий предъявлять следующие требования:
– условие КОЗ, а также полученный результат должны нести познавательную, развивающую и воспитывающую значимость, чтобы деятельность учеников, направленная на нахождение решения, была мотивированной;
– учащимся необходимо понимать ценность приобретения нового способа или же приема решения, который в дальнейшем можно использовать и в аналогичных ситуациях, иными словами, целью результата КОЗ не следует считать формальное получение ответа;
– формулировать задание необходимо в форме проблемы, которую учащимся предстоит разрешить, причем в тексте не должно содержаться явных указаний на ход решения;
– способ решения задания должен содержать в себе комбинацию уже известных способов, причем на выбор способа не накладываются ограничения;
– информация, представленная в задании, может быть как недостающей или избыточной, так и противоречивой;
– при завершении работы над компетентностно-ориентированным заданием необходимо учащимся продемонстрировать приобретенный в ходе работы набор знаний, умений и навыков;
– в связи с тем что результат выполнения задания должен нести в себе некую значимость, в конце необходимо указать на такие области, где может применяться полученный результат [9].
Оформлять компетентностно-ориентированные задания принято в соответствии с определенно построенной структурой. Создавая компетентностно-ориентированные задания, важно учитывать, что в процессе обучения школьникам необходимо осуществлять учебно-познавательную деятельность продуктивного характера. Следовательно, в процессе проектирования таких заданий можно задействовать проблемные, обучающие, поисковые КОЗ [9]. Заметим, что не существует готовых к внедрению в обучение в школе компетентностно-ориентированных зданий по стохастике, а есть только иллюстрации возможных реализаций компетентностного подхода. Представленные авторами задания отвечают целям изучения стохастического материала, а именно, развитию стохастической интуиции, формированию соответствующих взглядов о свойствах в окружающем нас случайном мире [9]. В качестве иллюстрации представим компетентностно-ориентированное задание «Попасть хотя бы раз» по теме «Испытания Бернулли», окончательное выполнение которого реализовано с применением пакета GeoGebra [10].
|
Формируемые компетенции
|
Познавательная: - уметь совершать поиск информации и выделять из нее необходимые сведения; - развитие памяти, внимания, выработка и критичность мышления; - ориентироваться на многообразие приемов решения задач; - развитие умения строить логические рассуждения. Коммуникативная: - уметь в достаточной степени полноты и точности высказывать свои мысли в согласии с задачами и требованиями коммуникации. Регулятивная: - намечать траектории развития с помощью включения в незнакомые виды деятельности. Личностная: - формирование твердой мотивации по реализации задания; - формирование когнитивного интереса. |
|
Стимул
|
Вероятность |
|
Задачная формулировка
|
Сколько потребуется орудий, чтобы шанс поражения цели при одном залпе был больше половины? |
|
Источник информации
|
Никольский С.М. Алгебра и начала математического анализа / С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин. М.: Просвещение, 2019. 431 с. |
|
Бланк выполнения задания |
Решение оформляется в виде отчета, в который включаются скриншоты вычислений. Для выполнения задания учащиеся используют любой доступный математический калькулятор (например, GeoGebra, Desmos). |
|
Инструмент оценивания
|
Модельный ответ Пусть событие Вероятность
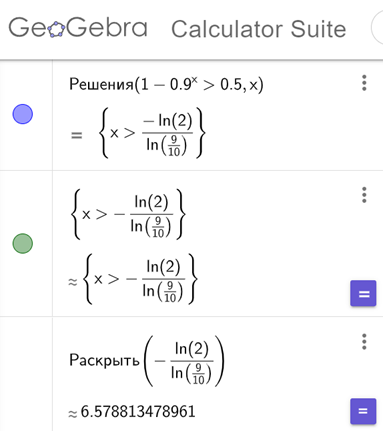
Она должна быть больше 0,5. Решаем соответствующее неравенство в GeoGebra (рис. 1). Получаем:
Рис. 1. Решение неравенства в GeoGebra Критерии оценивания: Последовательный алгоритм рассуждения решения задания − 1 балл. Понимание теоретических знаний и умение их применять при решении задания – 1,5 балла. Верно выполненные вычисления, в том числе в GeoGebra – 1 балл. Грамотное оформление задания − 1 балл. Самостоятельность при решении – 0,5 балла. Максимальное количество баллов − 5. |
Рассмотрим еще один пример КОЗ по теме «Испытания Бернулли», в которой могут присутствовать избыточные условия, однако они могут нести некоторую познавательную функцию межпредметного либо практического характера.
|
Формируемые компетенции
|
Познавательная: - уметь совершать поиск информации и выделять из нее необходимые сведения; - развитие памяти, внимания, выработка и критичность мышления; - развитие умения строить логические рассуждения. Коммуникативная: - уметь в достаточной степени полноты и точности высказывать свои мысли в согласии с задачами и требованиями коммуникации. Регулятивная: - планировать необходимые действия, операции, действовать по плану; - намечать траектории развития с помощью включения в незнакомые виды деятельности. Личностная: - готовность к действиям в условиях неопределенности; - формирование твердой мотивации по реализации задания. |
|
Стимул
|
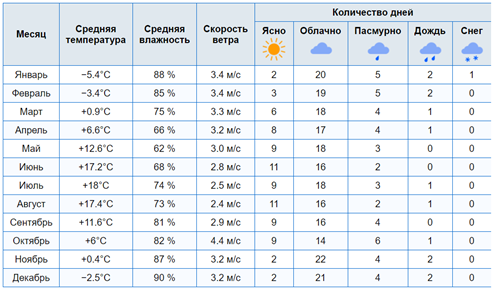
На рисунке представлена статистика погоды в городе Смоленске. По данным таблицы видно, что самым теплым месяцем является июль, самым холодным – январь. Больше всего солнца в Смоленске в июне и августе. Таким образом, июнь и август – самые солнечные месяцы в Смоленске.
|
|
Задачная формулировка
|
Какова вероятность того, что из семи наугад выбранных дней в мае три окажутся ясными? |
|
Источник информации
|
Авторская задача |
|
Бланк выполнения задания |
Решение оформляется в виде отчета. Для выполнения задания учащиеся могут использовать любой доступный математический калькулятор (например, GeoGebra, Desmos). |
|
Инструмент оценивания
|
Модельный ответ Событие А – 3 из 7 наугад выбранных дней в мае – ясные. По таблице находим, что в мае 9 ясных дней. Значит, вероятность ясного дня в мае: Вероятность, что из 7 наугад выбранных дней в мае 3 окажутся ясными, находится по формуле Бернулли: Подставив данные значения в формулу, получаем Критерии оценивания: Последовательный алгоритм рассуждения решения задания − 1 балл. Понимание теоретических знаний и умение их применять при решении задания – 1,5 балла. Верно выполненные вычисления – 1 балл. Грамотное оформление задания − 1 балл. Самостоятельность при решении – 0,5 балла. Максимальное количество баллов − 5. |
Заключение
Стохастические методы внедряются в практическую, профессиональную деятельность людей и тем самым приобретают все возрастающее значение. Компетентностный подход в условиях современного образовательного процесса является наиболее оптимальным для формирования стохастической компетентности школьников, так как учитывает не только содержательно-операциональный компонент учебной деятельности, но и мотивационно-ценностный и рефлексивно-оценочный. Это особенно важно при обучении стохастике, достаточно сложному для восприятия и овладения разделу математики. В качестве эффективных инструментов формирования стохастической компетентности мы выделяем интерактивные методы обучения и компетентностно-ориентированные задания. При построении стохастической модели задачи интерактивными методами ученику приходится самому понять ее реальное содержание, представив конкретную жизненную либо профессиональную ситуацию, требующую применения методов стохастики, провести исследование, эксперимент, поставить опыт, используя при этом современные информационные технологии.
Представленные в исследовании рекомендации по постановке и использованию компетентностно-ориентированных заданий способны улучшить эффективность обучения стохастике, а значит, и повысить уровень стохастической компетентности учащихся.
Библиографическая ссылка
Евдокимова Г.С., Сенькина Г.Е., Осипов Р.А. РАЗВИТИЕ СТОХАСТИЧЕСКОЙ КОМПЕТЕНТНОСТИ ОБУЧАЮЩИХСЯ В ОБЩЕМ ОБРАЗОВАНИИ: ВЫЯВЛЕНИЕ КРИТЕРИЕВ, ИНСТРУМЕНТОВ // Современные проблемы науки и образования. 2023. № 6. ;URL: https://science-education.ru/ru/article/view?id=33182 (дата обращения: 14.03.2026).
DOI: https://doi.org/10.17513/spno.33182




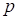 поражения цели при одиночном выстреле любого из n орудий равна 0,1.
поражения цели при одиночном выстреле любого из n орудий равна 0,1.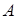 – при одновременном выстреле из n орудий цель будет поражена хотя бы одним из них. Найдем вероятность противоположного события
– при одновременном выстреле из n орудий цель будет поражена хотя бы одним из них. Найдем вероятность противоположного события 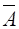 – цель не поражена. Это означает, что все орудия промахнутся.
– цель не поражена. Это означает, что все орудия промахнутся. 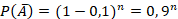 .
.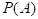 хотя бы одного попадания:
хотя бы одного попадания: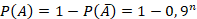 .
.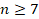 .
.
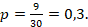 Вероятность того, что выбранный день не будет ясным:
Вероятность того, что выбранный день не будет ясным: 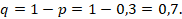
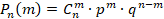 , где
, где 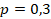 ,
, 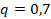 ,
, 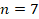 ,
, 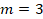 .
.