Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Проблема контроля знаний учащихся возникла давно, с той поры, когда появились первые образовательные учреждения. С развитием человеческого общества, появлением многочисленных институтов, школ, колледжей и других учреждений проблема становится все актуальнее.

В российских университетах внутренние методики обучения практически не менялись с 1930-х годов, что вызывает критику в свете несоответствия потребностям современного рынка труда. Выпускники сталкиваются с недостатком подготовки к профессиональным задачам, вынуждая бизнес тратить дополнительные ресурсы на их обучение. Следствием этого является снижение значимости университетских дипломов.

Сегодня, в эпоху цифровой экономики, наблюдаются быстрая эволюция технологий и появление новых профессий, таких как копирайтер, вебмастер, интернет-коуч, требующих новых умений и навыков. Для успешной адаптации к современным рыночным требованиям выпускникам необходимо не только обладать профессиональными знаниями и навыками, но и развивать гибкие компетенции. В этом контексте наиболее эффективным решением является использование индивидуальных образовательных траекторий (ИОТ).

Изучение высшей математики является важным компонентом и неотъемлемой частью образования студентов во многих областях знаний. Оно развивает важные навыки, которые пригодятся не только в академическом смысле, но и в профессиональной жизни. Математическое образование вносит значительный вклад в личностный и профессиональный рост студентов. Изучение высшей математики развивает абстрактное мышление и способность видеть закономерности во всем окружающем нас мире. Оно помогает студентам осознать, что многие явления и процессы можно представить в виде математических моделей, что позволяет сделать точные прогнозы и предсказания.

Высшая математика состоит из различных разделов, таких как линейная алгебра, математический анализ, аналитическая геометрия, теория вероятностей и статистика. Каждый из этих разделов имеет свои собственные принципы и методы, которые применяются в решении задач и проблем. Однако из-за сложности этой науки многие студенты испытывают трудности при ее изучении. Стоит также отметить, что в настоящее время процесс обучения на всех этапах един для всех учащихся по уровню содержания и сложности. Эта проблема касается и контроля – одинаковые измерительные материалы и критерии оценивания для всех студентов независимо от их индивидуальных особенностей, что усложняет получение достоверной информации о результатах учебной деятельности учащихся.

Для достижения поставленных задач при организации учебного процесса целесообразно учитывать принцип индивидуализации обучения. Это обусловливает создание системы обучения, которая адаптируется к уникальным потребностям каждого студента, помогая избежать несправедливого сравнения и оценки. Такой подход дает каждому учащемуся возможность раскрыть свой истинный потенциал. Очевидно, данный подход поможет решить проблему утраты интереса к образованию, так как каждому студенту будет предоставлена индивидуальная траектория, которая позволит достичь максимальных результатов.

Цель исследования

Цель настоящего исследования состоит в определении подходов к реализации индивидуальной образовательной траектории студентов при изучении дисциплины «Алгебра и геометрия» и построении индивидуальных маршрутов оценки образовательных достижений студентов по рассматриваемой дисциплине.

Материал и методы исследования

С целью оценки эффективности внедрения ИОТ в учебный процесс авторы статьи провели закрытое исследование в течение одного семестра группы из 24 студентов Пензенского государственного университета (ПГУ).

В процессе исследования использовались различные методы: анализ психолого-педагогической и математической литературы; наблюдение и обобщение опыта преподавания, моделирование индивидуальных траекторий оценивания образовательных достижений студентов.

Подробнее остановимся на понятии образовательной индивидуальной траектории. Индивидуальная образовательная траектория (ИОТ) – подход, при котором студент может самостоятельно формировать свою образовательную программу с учетом собственных интересов, целей и возможностей [1, 2]. Это перспективная стратегия цифровой трансформации науки ивысшего образования, предусматривающаяпереход обучающихся в вузах, подведомственных Минобрнауки России, к ИОТ ориентировочно к2030 году [2].

Основными характеристиками индивидуальной образовательной траектории являются: личная инициатива студента, проявление индивидуальности, адекватное восприятие мира и себя в этом мире, накопление различного учебного, социального и образовательного опыта.

В рамках ИОТ студенты могут получать персонализированную помощь и советы по своей образовательной траектории от преподавателя, что позволяет им лучше разобраться в своих сильных и слабых сторонах и выбрать оптимальные пути развития.

Индивидуальная образовательная траектория является важным инструментом для студентов, позволяющим им развить свои потенциальные возможности и достичь поставленных образовательных целей наиболее эффективным и интересным для них способом. Это способствует созданию качественного и гибкого образовательного процесса, который учитывает индивидуальные потребности и интересы каждого студента.

В качестве примеров реализации концепции индивидуального обучения и ИОТ можно привести следующие:

– концепция «Personalized Learning Pathways», разработанная компанией Summit Public Schools (США) для создания персонализированной образовательной модели, учитывающей индивидуальные потребности и интересы каждого ученика;

– Summit Learning: концепция, разработанная в США, предоставляющая ученикам возможность создавать свои собственные ИОТ с помощью онлайн-ресурсов и индивидуальной поддержки учителей. Эта концепция ставит целью помочь ученикам развиваться в соответствии с их сильными сторонами и интересами;

– концепция Adaptive Learning – разрабатывалась и реализовывалась в различных контекстах и организациях по всему миру. Adaptive Learning – это подход к обучению, основанный на использовании компьютерных технологий и алгоритмов, которые адаптируют образовательный процесс под индивидуальные потребности и способности каждого ученика. Множество университетов, исследовательских центров и компаний занимаются разработкой и применением Adaptive Learning. Некоторые из них включают Carnegie Mellon University, Massachusetts Institute of Technology (MIT), Stanford University, а также венчурные и инновационные компании в сфере образования;

– Competency-based Learning (Обучение на основе компетенций): концепция компетентностного обучения была разработана в разных странах, включая США, Канаду, Финляндию, Новую Зеландию и Австралию.

В российских психолого-педагогических исследованиях выделены следующие подходы к классификации индивидуальных образовательных маршрутов: на основании направленности образовательных интересов (Е.А. Александрова); интеллектуальная направленность деятельности (С.В. Маркова); по возрастному критерию (А.П. Тряпицына) [3, 4].

Рассмотрим реализацию данного подхода в процессе изучения курса «Алгебра и геометрия», в частности на этапе контроля сформированных знаний, умений и навыков.

Контроль выполняет четыре основные функции.

1. Определение уровня подготовки: контроль позволяет оценить степень усвоения учебного материала, умений и навыков, которые были сформированы в процессе обучения. Это дает возможность определить, насколько студенты готовы к следующему этапу обучения или к решению реальных задач в профессиональной деятельности.

2. Регуляция образовательного процесса: контроль позволяет выявить слабые места в обучении студентов и принять меры для их устранения. На основе результатов контроля можно скорректировать методы и технологии обучения, ввести дополнительные материалы или упражнения для более эффективного освоения учебного материала.

3. Мотивация студентов: контроль стимулирует студентов к активному и осознанному участию в образовательном процессе. Регулярная проверка знаний позволяет контролировать их успеваемость и отслеживать прогресс, что влияет на мотивацию к дальнейшему обучению.

4. Обратная связь: контроль предоставляет ученикам информацию о недостатках и ошибках в их знаниях, умениях и навыках. Это дает возможность студентам получить обратную связь от преподавателя, исправить ошибки и улучшить свою подготовку. Контроль также позволяет преподавателям анализировать результаты и предоставлять индивидуальное обучение, если это необходимо.

Рассмотрим реализацию индивидуальных маршрутов по дисциплине
«Алгебра и геометрия» на этапе контроля. Эффективным инструментом проверки качества усвоенных знаний является тестирование, подробнее остановимся на нем. Тесты считаются наиболее эффективным и объективным методом оценки, позволяющим не только определить уровень учебных достижений, но и анализировать структуру знаний и отклонения от нормы в ответах студентов на тестовые задания. Они обладают несколькими преимуществами по сравнению с другими методами оценки знаний: снижают временные и финансовые затраты на проверку знаний, способствуют определению индивидуального темпа обучения каждого студента, быстро выявляют пробелы в подготовке, а также мотивируют студентов к самоконтролю. Кроме того, системы тестирования могут использоваться для создания рейтингов, что является эффективным средством стимуляции учебной мотивации. Согласно педагогическим и методическим исследованиям, качество теста определяется такими параметрами, как надежность, валидность и эффективность [5].

Характеристика надежности теста определяется стабильными и устойчивыми показателями, получаемыми при проведениях повторных измерений при помощи одного и того же теста или его аналога. Повышение содержательного разнообразия тестовых заданий ведет к снижению надежности теста. Также на критерий надежности тестов значительное влияние оказывает сложность их выполнения. Наибольшую надежность и практическую ценность имеют тесты, в состав которых включены задания, на которые дают правильные ответы 50–85% обучаемых [6]. Следует также обозначить ряд показателей качества, предъявляемых к тестовым заданиям, согласно [7].

1. Адекватность целям проверки. При составлении задания выделяются существенные и несущественные признаки элементов знаний. Существенные признаки закладываются в эталонный ответ. В другие ответы закладываются несущественные признаки с учетом характерных ошибок. Если учащийся выделяет существенные признаки, а не формальные, то задание отвечает критерию адекватности целям проверки.

2. Определенность. После прочтения задания каждый учащийся понимает, какие действия он должен выполнить, какие знания продемонстрировать. Если учащийся после прочтения задания правильно действует и отвечает, задание считается определенным. Если на вопрос задания отвечает менее 70% учащихся, то его необходимо проверить на определенность.

3. Простота. Формулировки заданий и ответы должны быть четкими и краткими. Показателем простоты является скорость выполнения задания.

4. Однозначность. Задание должно иметь единственный правильный ответ-эталон.

5. Равная трудность. При составлении тестов в нескольких вариантах равная трудность определяется стабильностью по вопросам во всех вариантах одного и того же задания [7].

Результаты исследования и их обсуждение

Рассмотрим дисциплину «Алгебра и геометрия». Общая трудоемкость дисциплины составляет 5 зачетных единиц, 144 часа; состоит из следующих разделов:

Каждый раздел содержит теоретическую подготовку в виде лекций, предполагает отработку умений и навыков на практических занятиях и оценку качества усвоенных знаний. Традиционно всем студентам выдаются задания для контрольной работы одинаковой сложности, что не позволяет организовать оценку качества образовательных достижений студентов в контексте построения индивидуальной образовательной траектории для каждого учащегося. Поэтому необходимо организовать процесс следующим образом.

1. После изучения темы студенту предлагается пройти тест первого уровня. Минимальным порогом прохождения данного теста является верное выполнение 60% заданий, при этом он получает 40 баллов и переходит к выполнению теста второго уровня, который позволяет повысить рейтинг до 100 баллов.

2. В противном случае студенту необходимо вернуться к повторному изучению необходимых теоретических сведений, после чего заново пройти тест первого уровня. Данный процесс будет повторяться до тех пор, пока обучающийся не наберет необходимый минимум баллов.

В случае успешного прохождения теста первого уровня обучающийся переходит к тесту второго уровня с возможностью повышения рейтинга до 100 баллов.

Рассмотрим реализацию предложенной схемы на примере изучения темы «Матрицы. Определители». После изучения данной темы студенту предлагается пройти тест первого уровня, содержащий 20 вопросов и рассчитанный по времени на 45 минут. В тесте содержатся вопросы следующих видов:

– тесты опознания, в которых студенту задается вопрос, требующий альтернативного ответа: «да» или «нет», «является» или «не является», «относится» или «не относится» и т. п.;
– тесты различения вместе с заданием содержат ответы, из которых учащийся должен выбрать один или несколько вариантов ответа.

Если студент при прохождении теста первого уровня набирает минимум 60% верных ответов, то он получает возможность перехода к тесту второго уровня по этой же теме. В противном случае обучающийся должен вернуться к повторному изучению теоретических сведений по теме «Матрицы. Определители». Причем анализ допущенных ошибок позволяет выявить и обратить внимание на конкретные для определенного студента пробелы в теоретических знаниях. Например, при решении матричных уравнений студент допускает ошибку в нахождении обратной матрицы, тогда ему рекомендуется повторно изучить методы нахождения обратной матрицы и способы нахождения определителя. Затем, после успешного прохождения теста первого уровня, учащийся переходит к изучению новой темы.

Тесты второго уровня содержат 30 вопросов, рассчитаны на два академических часа и представляют собой вопросы следующих типов.

Множественный выбор с одним верным вариантом ответов: например, студенту необходимо выбрать из предложенного списка правильную формулу, утверждение, термин, числовой ответ и т.д.

Задание. Если определитель матрицы 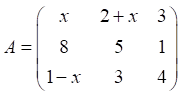равен «-11», то положительное значение x равно

Варианты ответов: 1) 4; 2) 8; 3) 2; 4) 6; 5) 13

Конструктивные и на подстановки: например, студент должен дописать необходимый элемент или элементы формулы, определения, теоремы.

Задание. Минор определителя – это:

Варианты ответов: 1) сумма элементов главной диагонали; 2) произведение элементов главной диагонали; 3) другой определитель, полученный из данного вычеркиванием строки и столбца; 4) алгебраическое дополнение элемента определителя.

Тесты-задачи с выборочными ответами. Этот тип заданий предполагает предоставление условия задачи вместе с необходимыми начальными данными, а в ответах студенту предлагается выбрать один из нескольких вариантов числовых или буквенных решений. Задача студента состоит в том, чтобы проанализировать предоставленную информацию и выбрать наиболее подходящий ответ из представленных вариантов, демонстрируя свои навыки решения и понимания материала.

Задание. Для матриц указать те операции, 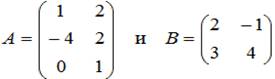которые можно выполнить. Ответ введите числом, записывая цифры в порядке возрастания.

Варианты ответов: 1) B · A; 2) B · AT; 3) BT · A; 4) BT · AT; 5) A · B; 6) AT · B; 7) A · BT

Если студент успешно прошел данное тестирование, то он повышает свой рейтинг (61–100 баллов) и переходит к изучению новой темы. Иначе с минимальным рейтингом 40 баллов также переходит к изучению новой темы.

В процессе реализации вышеизложенных положений авторами были сформированы методические указания к построению системы тестирования. Особенности содержания такой дисциплины, как «Алгебра и геометрия», обусловливают специфические подходы к разработке тестовых заданий. Выделим следующие значимые при разработке тестовых заданий по рассматриваемым дисциплинам особенности: большое количество числовой и формульной информации; формирование умений и навыков решения определенного класса задач; обилие специальной терминологии; необходимость в громоздких вычислительных операциях.

В частности, можно выделить следующие этапы разработки тестов по дисциплине «Алгебра и геометрия» (рисунок).

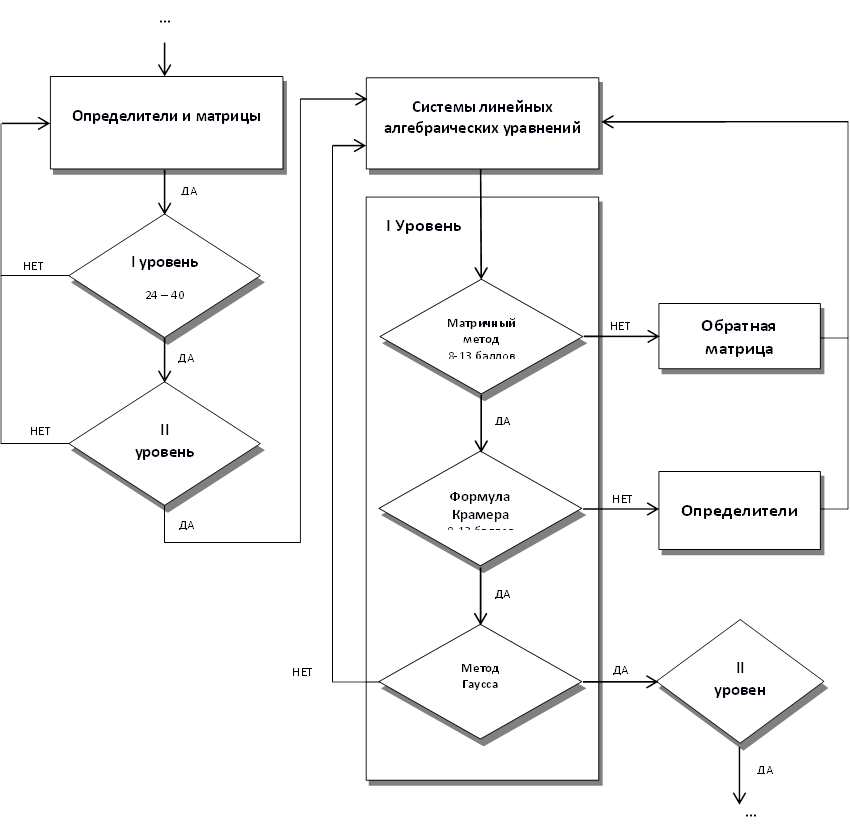Схема разноуровневого тестирования

В рассматриваемом ключе авторами статьи составлены методические рекомендации к разработке системы тестирования для построения индивидуальных маршрутов оценки образовательных достижений студентов по дисциплине «Алгебра и геометрия».

1. Определение цели и задачи тестирования: перед началом разработки системы тестирования необходимо определить основные цели и задачи, которые она должна решать. Например, это могут быть проверка знаний студентов по определенной теме, определение уровня подготовки учащихся для дальнейшей индивидуальной работы, оценка эффективности обучения и т.д. Уровень трудности тестового задания должен соответствовать уровню усвоения учебного материала с учетом реализации ИОТ.

2. Определение критерия оценки знаний: для того чтобы система тестирования была эффективной, необходимо определить критерии оценки знаний. Это могут быть критерии, связанные с количеством правильных ответов, скоростью выполнения заданий, уровнем сложности заданий и т.д. Методика оценивания ответов студентов должна быть простой, объективной и удобной для компьютерной обработки результатов тестирования.

3. Разработка тестовых заданий: для того чтобы система тестирования была эффективной, необходимо разработать качественные тестовые задания. Они должны быть разнообразными по форме и содержанию, позволяя оценить знания учащихся в различных аспектах и исследовать процесс усвоения студентами учебного материала по математике. Содержание должно отражать знания, умения и навыки по дисциплине «Алгебра и геометрия» которые необходимо проверить. Формулировка содержания тестового задания должна быть в виде кратких свернутых суждений и в повествовательной форме. Необходимо соблюдение единого стиля оформления тестового задания.

4. Разработка алгоритма выбора индивидуальной траектории обучения: для того чтобы система тестирования была адаптивной, нужно разработать алгоритм выбора индивидуальной траектории обучения. Он должен учитывать результаты тестирования и предлагать студентам задания, соответствующие их уровню знаний.

5. Проведение тестирования системы: перед внедрением системы тестирования необходимо провести ее проверку. Это позволит выявить ошибки и недостатки, а также определить эффективность системы.

6. Внедрение системы тестирования: после проведения тестирования и исправления ошибок систему тестирования можно внедрять в образовательный процесс. Следует провести обучение студентов работе с системой и обеспечить ее поддержку и сопровождение. Использование электронной системы тестирования позволяет интенсифицировать процесс обучения математики и эффективно организовать образовательную деятельность.

Выводы

Таким образом, в ходе исследования получены следующие результаты.

1. Построены индивидуальные маршруты оценки образовательных достижений студентов по дисциплине «Алгебра и геометрия» для студентов специальности 27.05.02 Метрологическое обеспечение вооружения и военной техники. 

2. Разработана и апробирована система многоуровневого тестирования по дисциплине «Алгебра и геометрия».

3. Составлены методические рекомендации к разработке системы тестирования для построения индивидуальных маршрутов оценки образовательных достижений студентов по дисциплине «Алгебра и геометрия».

Индивидуальная образовательная траектория (ИОТ) представляет собой инновационный инструмент, способный эффективно справляться с проблемой утраты интереса к обучению, предлагая каждому студенту интересный именно ему путь. Применение ИОТ способствует формированию у студентов интереса ксаморазвитию, критической оценки, готовности принимать решения инести заних ответственность. Как показывает наш собственный опыт преподавания, такой подход существенно интенсифицирует работу по систематизации математических знаний за счет разностороннего анализа ситуации и привнесения в этот анализ субъективно-личностного фактора.