Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Исследовательские умения являются базовыми для исследовательской деятельности, и их формирование актуально для обучающихся младших курсов. В процессе получения среднего общего образования происходит первое знакомство с учебно-исследовательской деятельностью. Учебной исследовательской деятельностью будем называть деятельность обучающихся, направленную на решение задачи путем творческой деятельности с заранее не известным результатом (в отличие от практикума, служащего для иллюстрации тех или иных законов природы) и предполагающую наличие основных этапов, характерных для исследования в научной сфере: постановка проблемы, изучение теории, посвященной данной проблематике, подбор методик исследования и практическое овладение ими, сбор собственного материала, его анализ и обобщение, собственные выводы [1, с. 5]. Современный ФГОС основного общего образования предусматривает формирование проектных и исследовательских умений в ходе создания каждым школьником индивидуального проекта, однако это направление работы стало обязательным для школьников относительно недавно и требует подготовки учителей к такой деятельности, тщательной отработки методики и технологии.

Для системы высшего образования характерна исследовательская деятельность студентов, однако часто она не охватывает всех обучающихся и в большей степени задействует обучающихся старших курсов. Как правило, несколько лучших студентов принимают участие в конкурсах исследовательских работ по итогам выполненных курсовых проектов и выпускных квалификационных работ. Формирование исследовательских умений играет существенную роль в педагогическом образовании, поскольку учителю предстоит развиваться на протяжении всей карьеры и познакомить учеников с научными исследованиями [2, 3]. Учебно-исследовательская работа обучающихся способствует повышению самостоятельности, активности и усилению самоконтроля.

Возрастание самостоятельности в выполнении экспериментально-исследовательских работ зависит от совокупности личностных значимых качеств обучающихся и может быть оценено методом экспертных исследований, описанных в [4]. Привлечение экспертов профессионального сообщества способствует объективной оценке сформированных умений учащихся и увеличению практико-ориентированности содержания учебных дисциплин и практик.

Разносторонние знания и глубокое осмысление математических теорий достигаются в процессе изучения профильных математических дисциплин, таких как алгебра и теория чисел, геометрия, математический анализ, и закрепляются при выполнении учебно-исследовательских проектов [5, 6].

Целью работы является описание формирования исследовательских умений у обучающихся посредством учебных дисциплин «Алгебра» и «Геометрия».

Материалы и методы исследования

Для выполнения исследования проведен анализ учебных пособий по вводному курсу математики и геометрии для педагогических вузов, заданий олимпиад и конкурсов, анализ педагогического опыта в процессе работы со студентами первого, второго и третьего курсов педагогического вуза в рамках преподавания дисциплин «Вводный курс математики», «Алгебра» и «Геометрия».

Результаты исследования и их обсуждение

Будем придерживаться следующих исследовательских умений, указанных в работе [7]:

· умение выделять подзадачи;

· умение задавать вопросы;

· умение выдвигать гипотезы;

· умение давать определение понятиям;

· умение классифицировать;

· умение делать выводы и умозаключения;

· умения и навыки работы с текстом;

· умение доказывать и защищать свои идеи.

ФГОС высшего образования (ядро педагогического образования) включает в себя компетенции, сопряженные с проектной и исследовательской деятельностью:

УК-1 – способен осуществлять поиск, критический анализ и синтез информации, применять системный подход для решения поставленных задач;

УК-2 – способен определять круг задач в рамках поставленной цели и выбирать оптимальные способы их решения, исходя из действующих правовых норм, имеющихся ресурсов и ограничений.

Рекомендации Министерства просвещения о содержании ядра педагогического образования содержат единые требования к наполнению профильных дисциплин в обязательной части учебного плана, что позволяет унифицировать содержание во всех педагогических вузах, обеспечить освоение необходимых для педагогической деятельности знаний, умений и навыков.

Выделим уровни усвоения компетенции УК-1 в дисциплинах «Вводный курс математики», «Алгебра», «Геометрия».

• Высокий (продвинутый). Соответствует оценке «отлично». Основные признаки выделения уровня: знает особенности системного и критического мышления, методы критического анализа и синтеза информации, методы и алгоритмы решения математических задач. Свободно демонстрирует умение аргументировать собственное суждение и оценивать информацию, обобщать, анализировать математические факты, методы, алгоритмы; формулировать задачу и осуществлять выбор соответствующего метода решения, выбрать нужную алгебраическую структуру в качестве модели задач. Свободно владеет навыком принимать обоснованное решение, навыками рефлексии мыслительной деятельности, основными законами логического мышления, методами выявления противоречий и достоверности суждений.

• Средний (оптимальный). Соответствует оценке «хорошо». Основные признаки выделения уровня: знает методы и алгоритмы решения математических задач, допускает незначительные ошибки. Демонстрирует умения анализировать математические факты, методы, алгоритмы; формулировать задачу и осуществлять выбор соответствующего метода решения. Уверенно владеет навыком принимать обоснованное решение, основными законами логического мышления, методами выявления противоречий и достоверности суждений допускает незначительные ошибки.

• Пороговый. Соответствует оценке «удовлетворительно». Основные признаки выделения уровня: не демонстрирует глубокого понимания материала о методах и алгоритмах решения математических задач. В основном демонстрирует умения применять методы, алгоритмы; осуществлять выбор соответствующего метода решения. Владеет основными законами логического мышления, допускает ошибки в построении логических рассуждений.

• Недостаточный. Соответствует оценке «неудовлетворительно» и характеризуется отсутствием признаков удовлетворительного уровня.

Выделим уровни усвоения компетенции УК-2 в дисциплинах «Алгебра», «Геометрия», «Вводный курс математики».

· Высокий (продвинутый). Соответствует оценке «отлично». Основные признаки выделения уровня: свободно демонстрирует умение определять совокупность взаимосвязанных задач и ресурсное обеспечение условия достижения поставленной цели. Свободно владеет навыком оценивать вероятные риски и ограничения, определять ожидаемые результаты решения поставленной цели.

· Средний (оптимальный). Соответствует оценке «хорошо». Основные признаки выделения уровня: демонстрирует умение определять совокупность взаимосвязанных задач и ресурсное обеспечение условия достижения поставленной цели. Уверенно владеет навыком оценивать вероятные риски и ограничения, определять ожидаемые результаты решения поставленной цели, допускает незначительные ошибки.

· Пороговый. Соответствует оценке «удовлетворительно». Основные признаки выделения уровня: не демонстрирует глубокого понимания, как определять взаимосвязанные задачи и условия достижения поставленной цели. Частично владеет навыком оценивать вероятные риски и ограничения, допускает ошибки в определении ожидаемых результатов решения задачи.

· Недостаточный. Соответствует оценке «неудовлетворительно» и характеризуется отсутствием признаков удовлетворительного уровня.

Усвоению универсальных педагогических компетенций способствует создание технопарков в педагогических университетах страны. Как показано в [8], технопарки дают возможность прохождения учебных практик проектно-исследовательского характера, способствуют расширению возможностей использования современного оборудования в учебных исследованиях и повышению мотивации к освоению педагогической профессии.

Цифровая образовательная среда активно проникает в традиционное образовательное пространство [9], что ставит новые задачи перед педагогическим сообществом и будущими учителями математики в том числе.

Онлайн-сервисы и калькуляторы оказались полезны при изучении математических дисциплин как во время аудиторных занятий, так и в самостоятельной работе школьников и студентов. Особенности применения графического калькулятора Desmos для создания интерактивного задания на построение графика функции описаны в [5]. В работе [2] рассмотрено использование среды GeoGebra и графического калькулятора Desmos в проектной деятельности по математике и моделировании, при осуществлении контроля решения задачи.

Рассмотрим возможности дисциплин обязательной части учебного плана для профиля «Математика», таких как «Алгебра» и «Геометрия», для формирования исследовательских умений на младших курсах. Базовые понятия логики высказываний и логики предикатов изучаются в педагогическом университете в начале обучения в курсе алгебры, а позднее расширяются в курсе математической логики. Как правило, рассматриваются основные логические операции и их свойства. Отметим, что построение умозаключений и понимание методов доказательств теорем невозможны без овладения логическим аппаратом. Полезно познакомить студентов с логическими операциями, не относящимися к основным: штрих Шеффера 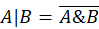и стрелка Пирса 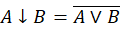– и предложить задание, требующее глубокого понимания свойств логических операций. Например, показать, что операция штрих Шеффера (или стрелка Пирса) образует полную систему связок сама по себе.

Для решения поставленной задачи требуется показать выражение конъюнкции и отрицания через штрих Шеффера: , .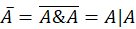

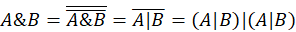Выполнение этого задания расширяет минимальный набор логических операций, позволяет уже на первых занятиях обсудить значимость рассматриваемых понятий, поработать с определениями понятий и выстраиванием логической цепочки рассуждений. Для выполнения задачи учащимся требуется выдвинуть гипотезу и подтвердить ее, выделить подзадачи: что значит полная система связок? Как взаимно выражаются изученные логические операции друг через друга?

Понятие «множество» является одним из основных в математике. Обучающиеся знакомятся с ним в школьном курсе, но более глубоко и строго изучают на первом курсе университета. В работе [10] подчеркнута роль этой темы в начале изучения математических дисциплин студентами вузов. Особый интерес представляет возможность использования свойств множеств при поиске решений нестандартных и олимпиадных задач, в том числе олимпиад школьников по математике. Одной из форм, позволяющих повысить мотивацию учащихся, а также познакомить с нестандартными формулировками заданий, являются олимпиады студентов. Соревнования дают возможность учащимся проявить себя, стать положительным примером для подражания. Олимпиады по педагогике, математике, информатике помогают формированию умения действовать в нестандартной ситуации. Совершенствование коммуникативных навыков учащихся, формирование умения распределять работу в группе происходят при организации работы в команде.

Отношение сравнения по модулю не рассматривают в базовом школьном курсе, знакомство с ним происходит также во введении в алгебру в теме «Множества», оно широко используется в теории чисел и в теории колец. Элементы 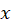и 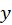сравнимы по модулю m, если их разность делится на m. Это записывают так: 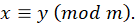Сравнения показывают важный пример колец, отличных от кольца целых чисел. Язык сравнений при работе со школьниками можно заменить на делимость. Таким образом, тематика сравнений и делимости может быть понятна старшим школьникам, с одной стороны, и знакомит с современными научными знаниями – с другой.

Процесс решения задачи требует исследовательского поиска метода решения, выдвижения гипотезы и анализа получающихся результатов для ее проверки. Выдвинутую гипотезу необходимо доказать, используя свойства математических объектов.

Использование теоретических фактов в нестандартных ситуациях способствует закреплению изученного материала. Отметим, что сравнения используются в современных научных исследованиях, например при поиске решений уравнений в целых числах.

Эффективным средством формирования исследовательских умений могут служить геометрические задачи на построение. Как минимум двум этапам схемы решения задачи на построение присущи элементы исследовательской деятельности. Кроме того, задачи на построение являются довольно сложными для школьного курса, а значит, требуют особенно тщательной проработки с будущими учителями математики как в курсе геометрии для глубокого осмысления теории, так и в курсе методики математики для освоения приемов обучения школьников решению таких задач.

На первом этапе решения задачи на построение путем анализа исходных данных задачи требуется выбрать оптимальный метод решения, не известный заранее. На этом этапе формируется умение выдвинуть гипотезу, классифицировать геометрические места точек, анализировать способы вычисления числовых характеристик фигур (длин, площадей, периметров).

На втором этапе происходит выполнение чертежа построения на основе анализа. Процесс построения требует разбить задачу на шаги, выполняемые с помощью циркуля и линейки, а значит, необходимо знание базовых задач на построение.

На третьем этапе необходимо выполнить доказательство того, что полученный объект удовлетворяет требованиям задачи. Здесь формируются умения делать выводы и строить умозаключения, доказывать свои идеи.

Цель последнего этапа решения задачи – исследования – состоит в необходимости ответить на два вопроса: при любых ли исходных данных задача разрешима и, если решения есть, то сколько их. Решение этих вопросов формируют умения анализировать данные, делать выводы и строить умозаключения, доказывать утверждения.

Отметим, что в задачах на построение для рационального решения часто требуется комбинация алгебраического метода и метода геометрических мест точек (пересечения фигур).

После изучения основных профильных курсов, таких как «Алгебра» и «Теория чисел», «Геометрия», «Математический анализ», студентам третьего и четвертого курсов предлагаются темы курсовых работ, которые, по сути, становятся важными учебно-исследовательскими проектами, демонстрирующими уровень сформированности исследовательских умений. Окончательный результат формирования исследовательских умений обучающихся оценивается в процессе выполнения и защиты дипломной работы. Тематику выпускных квалификационных работ рекомендуется согласовать с образовательными организациями.

Заключение

Описанный подход к подбору содержания и заданий учебных курсов способствует формированию исследовательских умений и позволяет учащимся легче включаться в работу по выполнению более крупных исследовательских проектов, проходить научно-исследовательскую и проектно-технологическую практику, подготовиться к профессиональной деятельности.