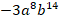На современную систему школьного образования возлагается ответственность за обеспечение условий для освоения обучающимися умения учиться, развития способности личности к самосовершенствованию, саморазвитию и самореализации. Для успешного освоения образовательной программы, достижения планируемых результатов, а также реализации профессиональных и жизненных планов в будущем каждый человек должен владеть регулятивными умениями, которые проявляются в способности ставить конкретную цель и формулировать задачи, планировать собственную деятельность для достижения цели, вносить определенные корректировки, предусматривать всевозможные варианты развития ситуации.
Анализ образовательной практики и научно-методических работ по проблеме формирования метапредметных образовательных результатов показывает, что реализация в процессе обучения комплекса средств и приемов диагностики и развития регулятивных универсальных учебных действий вызывает определенные затруднения у учителей математики [1, 2, 3].
Результаты диагностических и контрольных работ указывают на проблему недостаточной сформированности регулятивных универсальных учебных действий в условиях существующей образовательной практики. Например, в аналитических материалах результатов основного государственного экзамена (ОГЭ) по учебному предмету «Математика» разных регионов страны на протяжении последних лет подчеркивается недостаточный уровень регулятивных умений обучающихся, таких как: нахождение и исправление собственных ошибок, рациональная организация времени выполнения экзаменационных заданий, самостоятельное контролирование полученных результатов и др. [4, 5]. Ряд иностранных исследователей отмечают зависимость успешности обучения математике у обучающихся от сформировавшихся у них регулятивных умений [6, 7].
Цель исследования – предложить и обосновать методические подходы к диагностике и развитию регулятивных универсальных учебных действий на уроках математики.
Материал и методы исследования. Методологическую основу работы составили теоретические методы исследования. Проведены анализ, обобщение и систематизация научно-методической литературы, исследований отечественных и зарубежных авторов по проблеме формирования и диагностики метапредметных образовательных результатов и регулятивных умений обучающихся, а также данных статистических и методических отчетов по результатам итоговой государственной аттестации выпускников 9-го классов.
Результаты исследования и их обсуждение. Ряд исследователей отмечают, что регулятивные универсальные учебные действия (РУУД) являются опорой в управлении собственной учебной деятельностью и ключевым звеном в овладении предметными результатами [8]. Проблеме формирования РУУД у обучающихся общеобразовательной школы в 7–9-х классах на уроках математики посвящены исследования Е.А. Бараковой, С.П. Беребердиной, Е.А. Пустовит и др. Существуют различные подходы к структурированию РУУД обучающихся. Среди них выделим классификацию Л.И. Боженковой [9], а также группы авторов: А.Г. Асмолова, Г.В. Бурменской, И.А. Володарской, О.А. Карабановой, Н.Г. Салминой, С.В. Молчанова [10]; С.Г. Воровщикова, Е.В. Орловой [11]; О.В. Берсеневой, Н.А. Журавлевой, М.А. Кейв, Л.В. Шкериной [12] и др. Согласно Федеральному государственному образовательному стандарту основного общего образования (далее – ФГОС ООО) [13], овладение РУУД включает в себя самоорганизацию, самоконтроль, эмоциональный интеллект, принятие себя и других. На основе анализа результатов исследований в области формирования РУУД была уточнена структура РУУД обучающихся 7–9-х классов: целеполагание, планирование, прогнозирование, тайм-менеджмент, исполнение плана, контроль, коррекция, оценка [14].
Анализ учебников из Федерального перечня по математике позволил констатировать тот факт, что предлагаемый учебный материал дает возможность организовывать работу обучающихся по формированию РУУД на уроках математики. Однако со стороны педагога требуется дополнительная трансформация имеющегося учебного материала. Например, вместе с обучающимися можно формулировать цели учебной деятельности с использованием специализированных аннотаций, но задания с конкретными формулировками на эту группу умений отсутствуют в рекомендованных учебниках. Подчеркнем, что задачным материалом учебников не обеспечены некоторые группы умений сформулированной структуры РУУД: рациональное распределение собственного времени для реализации обозначенных шагов планов деятельности; осуществление контроля времени в соответствии с запланированным временем; оценивание результатов учебной деятельности с использованием цифрового образовательного ресурса; обращение за помощью в случае необходимости и др. В результате проведенного анализа учебников по математике для обучающихся 7–9-х классов был сделан вывод о необходимости обогащения задачного материала комплексом специализированных учебных задач и заданий, ориентированных на формирование РУУД у обучающихся. Приведем в качестве примера фрагмент разработки комплекса задач по теме «Синус, косинус, тангенс, котангенс угла», направленных на формирование РУУД у обучающихся 9-го класса, которые можно применять на уроках геометрии в качестве дополнительного материала.
Задание1. Определите, для чего необходимо знать формулу 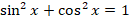 ?
?
Задание2. Установите и зафиксируйте последовательность шагов для решения следующей задачи: «Найдите 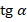 , если
, если 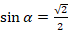 и
и 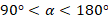 ».
».
Задание 3. Выполните задание по предложенной последовательности действий:
«Найдите 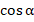 , если
, если 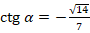 ».
».
1) Определить знак функции 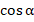 .
.
2) Найти 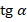 по формуле
по формуле 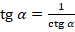 .
.
3) Воспользовавшись формулой 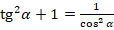 и подставив значение
и подставив значение 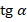 из пункта 2, найти значение
из пункта 2, найти значение 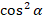 .
.
4) Определить значение 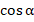 с учетом знака функции из пункта 1.
с учетом знака функции из пункта 1.
Задание 4. Дан ряд заданий по теме «Синус, косинус, тангенс, котангенс угла».
1) Определите примерное время, которое понадобится Вам для решения каждого из этих заданий (табл. 1).
Таблица 1
Задание 4 по теме «Синус, косинус, тангенс, котангенс угла»
|
№ |
Задания |
Примерное время |
|
|
«До» |
«После» |
||
|
1 |
Найдите значение выражения: а) |
|
|
|
2 |
Найдите |
|
|
|
3 |
Упростите выражение: а) |
|
|
|
4 |
Найдите значение выражения, не пользуясь таблицами и калькулятором: а) |
|
|
2) Запишите время, которое реально было потрачено на выполнение предложенных заданий.
3) Для решения предложенных заданий хватает ли Вам имеющихся теоретических знаний по теме?
4) Требуется ли Вам помощь со стороны учителя, одноклассников, ресурсов Интернета и т.д.?
Задание 5. Пройдя по ссылке https://learningapps.org/watch?v=pkdxy0z1n22, выполните задание, фиксируя решение в тетради. После его выполнения сравните ответ с эталоном на сайте. Внесите корректировки в Ваше решение в том случае, если были допущены ошибки.
На основе сформулированной структуры РУУД необходимо выделить критерии, показатели и уровни их сформированности, учитывая возрастные и психологические особенности обучающихся 7–9-х классов, предметное содержание учебного материала.
Критерии сформированности РУУД у обучающихся 7–9-х классов:
‒ умение организовывать учебную деятельность (КР1), включающее целеполагание, планирование, тайм-менеджмент и прогнозирование;
‒ умение управлять учебной деятельностью (КР2), включающее исполнение плана, тайм-менеджмент и контроль;
‒ умение осуществлять коррекционно-оценочную деятельность (КР3), включающее коррекцию и оценку.
Опорой для определения показателей и уровней сформированности РУУД у обучающихся 7–9-х классов, согласно предложенным критериям, являлись работы Г.М. Голубчикова, М.Г. Голубчиковой, Е.Л. Федотовой [15], В.А. Далингера, М.В. Дербуш, Р.Ю. Костюченко, С.Н. Скарбич, Т.П. Фисенко [16], Л.В. Шкериной [17]. В рамках исследования за основание выделения уровней примем степень самостоятельности выполнения действия (постоянные подсказки со стороны, частично самостоятельное и полностью самостоятельное), наличие результата выполнения действия (результат действия отсутствует, результат действия частично присутствует, результат действия полностью присутствует). Таким образом, низкий уровень выражается в невыполнении поставленной задачи обучающимся либо в выполнении задания в его малой доле, несмотря на помощь со стороны. Средний уровень будем интерпретировать как частичное выполнение поставленной задачи обучающимся, с возможными корректировками или подсказками со стороны учителя. Высокий уровень характеризуется полноценным выполнением поставленной задачи обучающимся самостоятельно, без посторонней помощи со стороны учителя или других взрослых, одноклассников.
На основе предложенных критериев, показателей и уровней сформированности РУУД у обучающихся, а также представленной в работе [14] динамической матрицы РУУД обучающихся, включающей содержание регулятивных действий обучающихся по классам, была разработана разноуровневая диагностическая карта РУУД обучающихся 7–9-х классов. В таблице 2 представлен ее фрагмент, содержащий критерий КР1.
Таблица 2
Разноуровневая диагностическая карта регулятивных универсальных учебных действий (фрагмент)
|
УУРД |
Уровни / дескрипторы уровней |
||
|
Низкий |
Средний |
Высокий |
|
|
КР1: умение организовывать учебную деятельность |
|||
|
Целеполагание |
Не формулирует цели и задачи учебной деятельности |
Формулирует цели и задачи учебной деятельности с помощью учителя |
Самостоятельно формулирует цели и задачи учебной деятельности |
|
Планирование |
Нецелесообразно или вовсе не составляет план учебной деятельности |
Частично самостоятельно, с подсказками со стороны учителя составляет план учебной деятельности |
Самостоятельно составляет план учебной деятельности |
|
Тайм-менеджмент |
Нерационально распределяет, несмотря на помощь со стороны, собственное время для выполнения плана учебной деятельности |
С помощью учителя рационально распределяет собственное время для выполнения плана учебной деятельности |
Рационально и самостоятельно распределяет собственное время для выполнения плана учебной деятельности |
|
Прогнозирование |
Не осуществляет прогнозирование учебной деятельности и не предвидит возможные трудности |
Прогнозирует учебную деятельность с помощью учителя и предвидит не все возможные трудности |
Самостоятельно прогнозирует учебную деятельность и предвидит возможные трудности |
В процессе развития РУУД у обучающихся 7–9 классов необходимо осуществлять контроль их сформированности через проведение диагностических работ. В рамках исследования были разработаны диагностические работы уровня сформированности РУУД у обучающихся 7–9-х классов. Диагностическую работу в каждом классе рекомендуется проводить во втором полугодии в зависимости от рабочей программы по алгебре и геометрии. В качестве примера рассмотрим диагностическую работу уровня сформированности РУУД у обучающихся 7-го класса. В таблице 3 представлена критериально-содержательная карта диагностической работы уровня сформированности РУУД у обучающихся 7-го класса.
Таблица 3
Критериально-содержательная карта диагностической работы уровня сформированности регулятивных универсальных учебных действий у обучающихся 7-го класса
|
№ задания |
|
Критерии сформированности регулятивных универсальных учебных действий |
|
|
1 |
КР1 |
Р1–1 |
умеет ставить цель учебной деятельности |
|
2 |
КР1 |
Р2–2 |
умеет составлять план учебной деятельности |
|
3 |
КР1 |
Р4–1 |
рационально распределяет время для реализации обозначенных шагов |
|
4 |
КР2 |
Р4–2 |
осуществляет контроль времени в соответствии с запланированным временем |
|
5 |
КР2 |
Р5–1 |
осуществляет действия в соответствии с планом |
|
6 |
КР1 |
Р3–1 |
прогнозирует учебную деятельность и предвидит возможные трудности |
|
7 |
КР2 |
Р6–1 |
осуществляет контроль учебной деятельности |
|
8 |
КР3 |
Р7–1 |
корректирует действия в результате обнаружения ошибок |
|
9 |
КР3 |
Р8–1 |
оценивает результаты учебной деятельности |
В таблице 4 представлен вариант диагностической работы уровня сформированности РУУД у обучающихся 7-го класса.
Таблица 4
Диагностическая работа уровня сформированности регулятивных универсальных учебных действий для 7-го класса
|
1 |
Учитель на уроке по теме: «Приведение подобных слагаемых» на доске написал следующее и сформулировал задание:
После самостоятельного выполнения задания обучающимися учитель озвучил правильное решение данного задания и попросил подчеркнуть ошибки в случае их нахождения. Определите цели выполнения данного задания: 1) закрепить вычислительные навыки; 2) закрепить навыки по теме «Приведение подобных слагаемых»; 3) познакомиться с правилом приведения подобных слагаемых; 4) формировать умение осуществлять контроль своих действий через сравнение с эталоном; 5) закрепить умение осуществлять подстановку числовых значений вместо буквенных переменных |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
Восстановите порядок действий (план своих действий) при сложении (вычитании) десятичных дробей, используя предложенные ниже шаги: 1. Дополнить недостающие разряды нулями. 2. Запятую в результате поставить под запятыми дробей. 3. Одноименные разряды записать друг под другом. 4. Сделать вывод о результате сложения (вычитания). 5. Сложить (вычесть) дроби поразрядно (как натуральные числа) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
3 |
Ознакомьтесь с заданием 5 и предположите примерное время на его выполнение, зафиксируйте примерное время в таблице в первом столбике.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
4 |
Запишите в таблицу (задание 3) во второй столбик, сколько составляет фактически затраченное время на выполнение задания 5. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
5 |
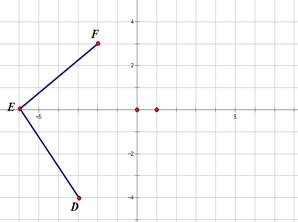
Перед выполнением задания обратите внимание на задания 3 и 4. Дан фрагмент чертежа.
Выполните следующие действия согласно следующему плану: 1. Отметьте точку 2. Подпишите получившуюся точку. 3. Отметьте точку 4. Подпишите получившуюся точку. 5. Отметьте точку 6. Подпишите получившуюся точку. 7. Соедините последовательно получившиеся точки с уже имеющимися точками |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
6 |
Спрогнозируйте все возможные ошибки, которые можно допустить при выполнении следующего задания:
Упростите выражение |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
7 |
Укажите номера уравнений, при решении которых были допущены ошибки:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
8 |
В предложенном варианте решения задания имеется ошибка. Скорректируйте решение задания в случае ее обнаружения. Упростите выражение
Решение:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
9 |
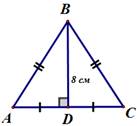
Оцените решение задачи в соответствии с предложенными критериями, запишите количество баллов, на которое вы оценили решение этой задачи. Обоснуйте свой ответ. В равнобедренном треугольнике
Решение. 1) 2) 3)
4) Ответ:
2 – ход решения верный, все его шаг выполнены правильно, получен верный ответ. 1 – ход решения верный, все его шаги выполнены правильно, но даны неполные объяснения или допущена одна вычислительная ошибка. 0 – решение не соответствует ни одному из критериев, перечисленных выше |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Для оценивания диагностической работы РУУД у обучающихся 7-го класса в таблице 5 сформулированы критерии и баллы.
Таблица 5
Оценочная карта диагностической работы регулятивных универсальных учебных действий обучающихся 7-го класса
|
№ задания |
Критерии для оценки |
Баллы |
|
1 |
Указаны ответы 2 И 4 |
2 |
|
Указан ответ 2 ИЛИ 4 |
1 |
|
|
Не указаны правильные ответы или ответ не дан |
0 |
|
|
2 |
Последовательность действий составлена правильно, т.е. 31524 |
2 |
|
Последовательность действий составлена частично правильно (3–4 позиции) |
1 |
|
|
Последовательность действий составлена неверно |
0 |
|
|
3 |
Ожидаемое и фактическое время совпадает ИЛИ второе меньше не более чем на 20% |
2 |
|
Фактическое время меньше ожидаемого, отличается на 21–50% ИЛИ фактическое время больше ожидаемого, но не более чем на 20% |
1 |
|
|
Ни один из критериев не выполняется |
0 |
|
|
4 |
Осуществляет контроль времени, запись ожидаемого и фактического времени присутствует |
2 |
|
Присутствует запись только одного из времени – фактического или ожидаемого |
1 |
|
|
Запись ожидаемого и фактического времени отсутствует |
0 |
|
|
5 |
Чёткое, последовательное и правильное выполнение действий в соответствии со всеми шагами предложенного плана
|
2 |
|
Имеются незначительные отклонения от порядка выполнения действий по предложенному плану |
1 |
|
|
Неправильное выполнение действий по предложенному шагу |
0 |
|
|
6 |
Указаны больше трех ошибок при выполнении задания |
2 |
|
Указаны 1–3 ошибки при выполнении задания |
1 |
|
|
Не указаны ошибки при выполнении задания |
0 |
|
|
7 |
Выбраны варианты ответа 1, 3 И 4 |
2 |
|
Выбраны один ИЛИ два варианта из трех вариантов ответа |
1 |
|
|
Не указан ни один из правильных вариантов ответа |
0 |
|
|
8 |
Обнаружена ошибка в рассуждении и полностью скорректировано решение, получено |
2 |
|
Обнаружена ошибка в рассуждении, но скорректированное решение не доведено до конца |
1 |
|
|
Ни один из критериев не выполняется |
0 |
|
|
9 |
Задача оценена верно по критериям с обоснованием оценки (поставили 0 баллов, так как ход решения верный, но нет объяснений, имеется вычислительная ошибка) |
2 |
|
Задача оценена верно, но без обоснования оценки |
1 |
|
|
Ни один из критериев не выполняется |
0 |
С помощью таблицы 6 можно определить уровень сформированности РУУД у обучающихся 7-го класса по каждому критерию.
Таблица 6
Определение уровня сформированности регулятивных универсальных учебных действий у обучающихся 7-го класса по каждому критерию (в баллах)
|
|
Низкий уровень |
Средний уровень |
Высокий уровень |
|
КР1 |
0–4 |
5–7 |
8 |
|
КР2 |
0–3 |
4–5 |
6 |
|
КР3 |
0–2 |
3 |
4 |
Таким образом, описанная деятельность с поэтапной диагностикой сформированности определенных метапредметных умений и фиксацией достижений обучающихся позволит учителю организовать целенаправленную работу по развитию регулятивных универсальных учебных действий на уроках математики. На основе полученных результатов педагог имеет возможность осуществлять корректировку методов и приемов преподавания на уроках математики, отслеживать динамику освоения результатов каждого обучающегося, а также работать над совершенствованием каждого умения.
Заключение. Проведенное исследование позволило определить подход к структурированию регулятивных универсальных учебных действий. На основе анализа научно-методической литературы, требований федеральных государственных образовательных стандартов и результатов образовательной практики дана характеристика критериев, показателей и уровней сформированности регулятивных универсальных учебных действий. Представлены авторские методические материалы для диагностики и развития регулятивных действий в рамках учебного предмета «Математика», в которых реализованы описанные теоретические положения.
Библиографическая ссылка
Гиматдинова Г.Н., Шашкина М.Б. ДИАГНОСТИКА И РАЗВИТИЕ РЕГУЛЯТИВНЫХ УНИВЕРСАЛЬНЫХ УЧЕБНЫХ ДЕЙСТВИЙ ОБУЧАЮЩИХСЯ НА УРОКАХ МАТЕМАТИКИ В 7-9 КЛАССАХ ОБЩЕОБРАЗОВАТЕЛЬНОЙ ШКОЛЫ // Современные проблемы науки и образования. 2023. № 6. ;URL: https://science-education.ru/ru/article/view?id=33074 (дата обращения: 14.03.2026).
DOI: https://doi.org/10.17513/spno.33074




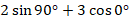 ; б)
; б) 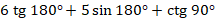
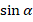 , если
, если 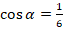
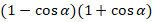 ; б)
; б) 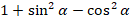 ;
; 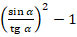
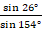 ; б)
; б) 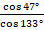 ; в)
; в) 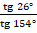 ; г)
; г) 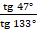
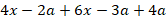 , если
, если 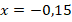 ;
;  .
.
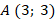 .
.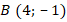 .
.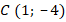 .
.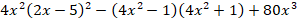
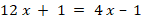
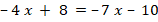
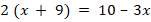
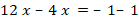
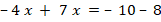
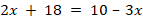
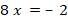
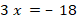
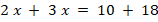
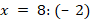
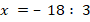
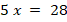
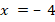
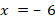
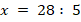
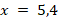
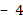 .
.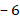 .
.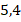 .
.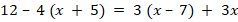
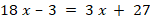
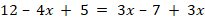
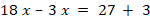
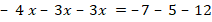
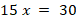
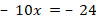
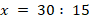
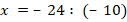
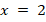
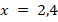
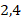 .
.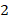
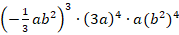
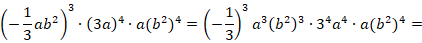
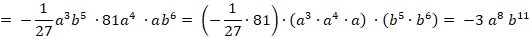
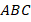 к основанию
к основанию 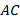 проведена высота
проведена высота 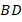 , равная 8 см. Найдите периметр треугольника
, равная 8 см. Найдите периметр треугольника 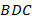 , если периметр треугольника
, если периметр треугольника 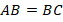
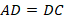
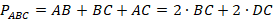
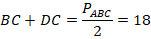
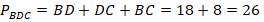 см.
см.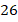
 Содержание критерия
Содержание критерия