Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

В обществе на современном этапе наблюдается возрастание роли теории вероятностей. Это объясняется тем, что знания и умения из этой области математики имеют большую прикладную направленность, помогают критически анализировать информацию и понимать вероятностный характер многих реальных событий и явлений. Начиная с 2003 года общеобразовательные учреждения поэтапно включают элементы комбинаторики, статистики и теории вероятностей в содержание учебного предмета «Математика» предметной области «Математика и информатика» уровня основного общего образования. А с 2021 года в ФГОС ООО обозначен обязательный учебный курс «Вероятность и статистика» наряду с традиционными «Алгебра» и «Геометрия». Тем не менее на сегодняшний день у преподавательского сообщества остается еще достаточно много вопросов, касающихся обучения теории вероятностей. Не исключено, что это является следствием отсутствия глубоких традиций методики преподавания, а также недостаточного количества учебных и учебно-методических материалов по этому разделу математики. Опыт преподавания показывает, что теория вероятностей остается сложным для усвоения обучающимися разделом.

Одним из возможных вариантов решения этой проблемы является, по мнению авторов, совершенствование дидактических средств путем применения визуальных моделей учебной информации.

Вопросы эффективности технологии визуализации учебной информации обсуждаются в научном сообществе с различных аспектов: различные техники визуализации и их роль в учебном процессе [1]; методы визуализации информации и их роль в формировании универсальных учебных действий при обучении математике [2]; эффективность применения приемов визуализации информации для формирования естественно-научной грамотности [3] и др. В то же время вопрос о применении визуальных моделей учебной информации в процессе обучения теории вероятностей раскрыт недостаточно полно.

Цель исследования – показать различные варианты использования визуальных моделей при обучении теории вероятностей.

Материалы и методы исследования. В основу исследования был положен теоретический анализ научных трудов в области использования средств визуализации для организации учебного процесса, сравнительный анализ учебно-методических комплектов (УМК) по алгебре и теории вероятностей, а также такие методы исследования, как абстрагирование и обобщение.

Результаты исследования и их обсуждение

В ходе изложения продемонстрируем использование визуальных моделей на примере УМК, в которых прослеживается традиционный для высшей школы способ изложения учебного материала.

В учебном пособии Г.К.Муравина и др. [4] сначала учащиеся на примере подбрасывания монеты знакомятся с равновероятными возможностями. Затем отмечается, что возможности не всегда являются равными, какие-то являются менее вероятными, а другие более вероятными. В следующем параграфе вводится классическое определение вероятности события формулой со словесным описанием. Подчеркивается, что «менее вероятные» и «более вероятные» – это очень неопределенные характеристики для сравнения вероятности различных событий. В математике у вероятности события, конечно, должна быть числовая характеристика.

Здесь, кроме определений и примеров, можно использовать графический образ рассматриваемых понятий – шкалу вероятностей (рис. 1).

Рис. 1. Шкала вероятностей

При вычислении вероятности естественным образом возникает проблема подсчета как всех возможностей, когда событие может произойти, так и общего числа всех возможностей. Решение этой проблемы – основные комбинаторные правила и формулы. В пособии Г.К.Муравина и др. [4] формулируется правило произведения, а также вводятся понятия перестановки, размещения, сочетания и формулы для вычисления их числа с общепринятыми обозначениями. Приводится также формула, определяющая число сочетаний через отношение числа размещений к числу перестановок: .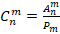

Следует отметить, что высказываются и другие точки зрения на использование традиционных комбинаторных обозначений в школьном курсе математики [5, с. 8]. Исключение предлагается сделать только для символа, обозначающего число сочетаний. Использование всех символов (а их здесь всего три) ненамного расширяет список обозначений, но не должно приводить к их путанице, если нет путаницы на уровне самих понятий, их сходства и различий. Однако авторы разделяют мнение о том, что в этой теме следует избегать других обозначений, например для числа сочетаний еще одного распространенного обозначения .

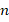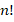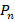Авторы УМК Ю.М.Колягина и др. [6] рассматривают вначале основные комбинаторные понятия: сочетания, размещения, перестановки для множества, состоящего из трех элементов, на примере задач с похожим содержанием. Формулы для подсчета числа различных комбинаций не приводятся, исключение делается только для числа перестановок из элементов. Вводятся обозначения и . Для организации вычисления числа комбинаций из данных элементов авторы предлагают воспользоваться таблицей вариантов и деревом вариантов, вводя при этом понятие графа.

Рассмотрим, например, классическую в теории вероятности задачу. Бросают два кубика: красный и синий. Считая все комбинации цифр на красном и синем кубике равновероятными событиями, составим таблицу всех возможных 36 исходов, изображенную на рисунке 2. В каждой ячейке таблицы находится сумма выпавших очков на обоих кубиках – от 2 до 12.

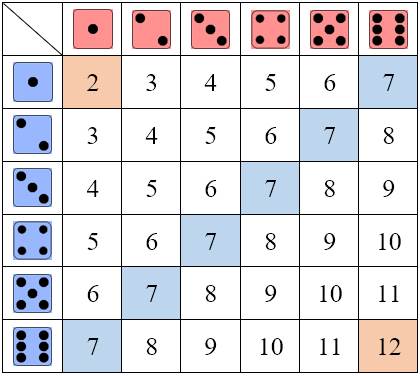
Рис. 2. Таблица всевозможных исходов

Из таблицы видно, что наименее вероятные исходы при броске двух кубиков – это 2 либо 12 (обозначены оранжевым цветом), так как для них существует только по одному варианту. Следовательно, вероятность каждого из этих событий равна 1/36. Наиболее вероятный исход – выбросить 7 (обозначены синим цветом), для него есть 6 вариантов, поэтому вероятность этого события равна 6/36 или 1/6.

Представленная таблица служит визуальной моделью множества всех возможных исходов, по которой несложно вычислить и количество комбинаций, благоприятствующих наступлению того или иного события.

С помощью таблиц возможно подсчитывать комбинации, составленные лишь из двух элементов. Для трех и более элементов целесообразнее познакомить учащихся с другой визуальной моделью – деревом вариантов, являющимся частным случаем графа. Название «дерево» отражает ветвящийся характер полученной структуры. Оно не только позволяет наглядно представить все возможные комбинации, но может пригодиться и в дальнейшем при изучении зависимых и независимых событий, условной вероятности, теоремы умножения вероятностей и формулы полной вероятности, «превратившись» в дерево вероятностей.

Рассмотрим процесс построения дерева вероятностей на конкретной задаче (урновая модель). В двух корзинах находятся шары разных цветов. В первой корзине – белые и черные шары с номерами 1, 2, 3, а во второй – красные, синие и белые с номерами 1 и 2. Найти вероятность того, что наудачу выбранный шарик будет из 2-й корзины, красного цвета, с записанным на нем номером 1.

Для построения дерева вероятностей от начальной точки графа проводят линии – рёбра, отражающие все возможные исходы события (рис. 3). Это первый этап. Каждый исход первого этапа служит новой отправной точкой, и уже от нее расходятся линии к возможным исходам следующего – второго этапа. Таких этапов или состояний может быть несколько. Над каждым ребром подписывают соответствующие вероятности, которые могут быть даны или их несложно найти из условия задачи. На примере такого графа наглядно показывается, как вероятность одного события может зависеть от предшествующего ему события – условная вероятность.

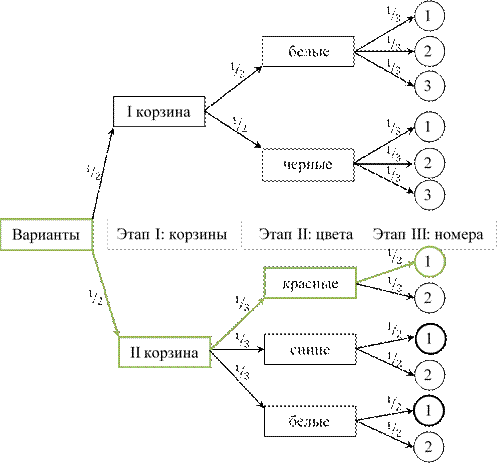
Рис. 3. Дерево вероятностей

Чтобы вычислить вероятность того, что наудачу выбранный шарик будет из 2-й корзины, красного цвета, с записанным на нем номером 1, перемножим вероятности, которые расположены вдоль выделенной зеленой линии (цепочки графа):

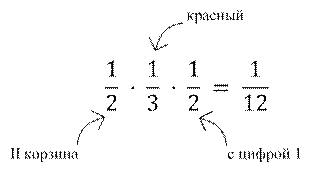В рассмотренной задаче дерево вероятностей используется в качестве опоры для поиска решения. Но оно может содержаться и в условии задачи. Так, в пособии «Математика. Вероятность и статистика. 7–9-е классы» под редакцией И.В.Ященко [7] приведены разнообразные задачи с деревом вариантов (деревом случайного опыта). Например, в задаче 113 [7, с. 42] требуется по изображению дерева некоторого случайного опыта найти вероятность события F (рис. 4).

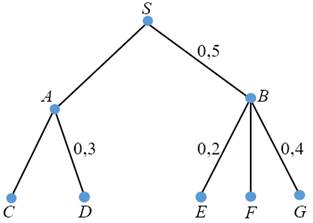
Рис. 4. Дерево случайного опыта

При решении этой задачи необходимо руководствоваться следующими правилами:

1. При построении дерева случайного опыта нужно следить, чтобы сумма вероятностей около всех ребер, выходящих из одной вершины, была равна единице (так как сумма вероятностей всех элементарных событий, образующих полную группу, равна единице).

2. Найти вероятность элементарного события можно с помощью правила умножения вероятностей: нужно найти произведение условных вероятностей вдоль соответствующей цепи.

3. Чтобы найти вероятность события с помощью дерева, нужно сложить вероятности всех цепочек, ведущих к этому событию от начальной вершины [7, с. 40-41].

Стоит обратить внимание, что разнообразие задач в указанном учебном пособии предварительно сопровождается достаточно подробным рассмотрением тем «Графы» и «Деревья».

К использованию дерева вероятностей могут приводить также задачи с условием, содержащим рисунок. Приведем пример. На рисунке 5а изображен лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может, поэтому на каждом разветвлении он выбирает один из путей, по которому еще не полз. Считая выбор дальнейшего пути чисто случайным, определите, с какой вероятностью паук приползет к выходу D.

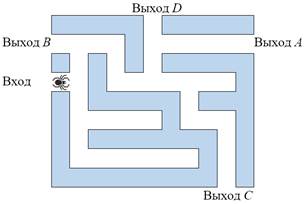
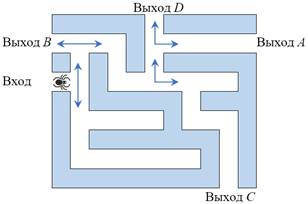
а) б)

Рис. 5. Лабиринты к задаче

Для решения задачи расставим на перекрестках стрелки, по которым может двигаться паук к выходу D (рис. 5б). Отметим на каждом из перекрестков одно направление из двух возможных, по которому будет двигаться паук. Очевидно, что вероятность в этом случае будет равна

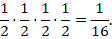
В ряду возможных визуальных моделей к задачам по теории вероятностей также можно упомянуть известные диаграммы Эйлера-Венна, которые не только отображают в виде некоторой замкнутой области множество всех элементарных исходов, но и помогают проиллюстрировать операции над событиями.

Изложенный материал будет не полным, если не отметить дидактические возможности современных цифровых технологий, которые позволяют не только создавать динамические визуальные модели, но и расширить опытно-экспериментальную часть учебного процесса, усиливающую его исследовательский характер (например, подробнее см.в [8]).

Заключение. Таким образом, визуальные модели не просто иллюстрируют математические факты из теории вероятностей, но и служат опорой при решении задач, способствуют активизации мыслительной и познавательной деятельности обучающихся. Для лучшего усвоения учебного материала визуальные модели, по мнению авторов, должны присутствовать в различных компонентах задачи (условие, решение, ответ), так как это позволяет учесть индивидуальные познавательные особенности обучающихся.