Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

В настоящее время объективной особенностью учебного процесса в техническом вузе стало значительное уменьшение времени аудиторной учебной работы студентов. Наряду с этим специалистами отмечаются слабая математическая подготовка и несформированность умений учебной деятельности у многих студентов младших курсов, поступивших в вуз [1,2]. Эти факторы негативным образом сказываются на качестве освоения обучающимися учебного материала. Вместе с тем, по мере изучения теоретического и практического содержания основных разделов курса математики студенты должны получить навыки использования прикладных компьютерных программ, поскольку это является важной основой профессиональных компетенций будущих инженеров.

Очевидно, что оптимальной можно считать такую учебную ситуацию, когда функциональные возможности программного обеспечения могут быть реализованы в ходе освоения теоретического материала и практических методов решения задач. Объективно потребности в программном сопровождении решения задач увеличиваются по мере продолжения обучения и усложнения содержания осваиваемых дисциплин. Важным является то, что многие программные математические средства, которые необходимы в будущей профессиональной работе обучающихся, например MathCAD, MATLAB и другие, обычно изучаются непосредственно на практических занятиях в учебном заведении. И именно в этом сегменте учебного процесса проявляется проблема, обусловленная недостатком времени аудиторной работы, которая ведет к формализму умений использования прикладных программ. Суть проблемы заключается в том, что обучающиеся осваивают теоретическую основу какого-либо раздела, приемы решения соответствующих задач, но при этом у них отсутствует практика осознанного применения основных функций прикладных программных пакетов. Либо, наоборот, в процессе использования программных математических пакетов обучающиеся получают возможность находить ответ в поставленной задаче, но при этом не понимают теоретических основ алгоритмов решений и выполняемых действий. Очевидно, что получение итогового значения того или иного искомого параметра с использованием встроенных программ, без представления о математической сущности теоретического и практического содержания, ведет к формальному освоению учебного материала и его быстрому забыванию.

Цель исследования ‒ обосновать основные направления методической работы преподавателя по освоению обучающимися встроенных программных пакетов математической среды MathCAD на занятиях в условиях значительного ограничения учебного времени.

Методы исследования: анализ условий учебной деятельности студентов, экспертная оценка, выполнение обучающимися экспресс-заданий на практических занятиях.

Работа проводилась во время практических занятий со студентами Уральского государственного университета путей сообщения, обучающихся по направлению подготовки «Подвижной состав железных дорог», в пределах нормативного времени, предусмотренного учебной программой: одно двухчасовое занятие аудиторной работы в две недели. Таким образом, обучающиеся имели доступ к лицензионному прикладному программному пакету MathCAD 1 раз в 2 недели. В ходе исследования наблюдалась группа студентов 2-го курса в количестве 70 человек.

Анализ выделенных выше факторов, сопровождающих учебный процесс, позволил сделать вывод о необходимости выбора небольшого по объему сегмента в изучаемом материале, понятного всем обучающимся в практическом исполнении, применительно к которому можно использовать функциональный аппарат программного пакета MathCAD.

Практика показывает, что значительный рост востребованности численных и программных методов проявляется при изучении учебного материала из раздела математической статистики. На этапе освоения способов обработки данных обучающиеся знакомятся с понятиями математических параметров и алгоритмами их нахождения. В этот период приходится выполнять большой объем «ручной», часто рутинной, работы с массивами данных [3]. Заметим, что многие программные продукты позволяют сразу извлечь необходимые математические параметры, которые описывают основные свойства выборки. Прежде всего, это статистические параметры: выборочная средняя, дисперсия, среднеквадратическое отклонение и др. [4,с.283–285]. Безусловно, такие программы являются удобным инструментом, значительно ускоряющим математическое описание изучаемых объектов. Однако, как показывает опыт, использование готовых программных функций без предварительного изучения теоретических основ процесса обработки данных нецелесообразно, так как ведет к формализму практического применения математических пакетов.

В ходе анализа учебного материала была выделена не сложная, но довольно трудоемкая промежуточная локальная задача, которую приходится решать практически всем обучающимся: составление вариационного ряда ‒ упорядоченного множества исходных данных. Отметим важные методические особенности этой промежуточной задачи. Во-первых, она функционально понятна всем обучающимся, поскольку не выходит за границы их субъективного опыта. Во-вторых, в ходе «ручной» работы нетрудно убедиться в том, что потребность машинного способа упорядочения элементов возрастает с увеличением числа данных. В-третьих, реализация функциональных возможностей математического пакета обладает значительным обучающим потенциалом, дифференцируемо реализуемым, в зависимости от уровня подготовленности обучающихся и имеющегося на его освоение времени.

Составление вариационного ряда – это первый этап обработки экспериментальных данных, как правило, представленных в некоторой таблице. Упорядоченное расположение значений измеряемой величины ‒ экспериментальных данных – значительно облегчает первоначальную оценку содержания выборки [5]. Практика показывает, что упорядочение данных обучающиеся обычно проводят вручную. Для выявления условий, способствующих более эффективному восприятию учебной задачи и результатов использования программных функций, им были предложены экспресс-задания, в которых было необходимо упорядочить по величине множество данных, представленное в произвольном виде. Результаты выполнения заданий показали, что подавляющее большинство обучающихся в случае наличия большого числа данных (10 и более) итоговый результат представляют в виде таблицы с несколькими строками и столбцами, в которой все элементы расположены в порядке сплошного возрастания их значений от столбца к столбцу или от строки к строке. Наименьшее значение измеряемой величины находится в левом верхнем углу таблицы, а наибольшее – в правом нижнем углу. Кроме того, если предложенный для сортировки исходный массив данных имел значительный объем и был представлен в виде матричной таблицы с определенным числом строк и столбцов, то практически все обучающиеся итоговый результат также представляли в аналогичной матричной форме такой же размерности. Очевидно, что такой вид привычен для обучающихся. Это позволяет сделать вывод о том, что наиболее удобной для дальнейшей работы формой упорядоченного массива данных будет его наглядное представление в виде двумерной матрицы со сквозным упорядочением всех элементов по строкам или столбцам, поочередно от ряда к ряду.

Именно здесь выявляется важная в рамках данной учебной задачи проблема. Дело в том, что в программном пакете MathCAD упорядочение элементов матрицы предполагает только сортировку столбцов по элементам выбранной строки с помощью встроенной функции rsort(A,i) или аналогичную сортировку строк по элементам выбранного столбца с помощью функции csort(A,i) [6]. Сквозного упорядочения сразу всех элементов двумерной матрицы массива данных, в привычном понимании, начиная с элемента, находящегося в верхнем левом углу и далее по чередующимся столбцам или строкам, в программной базе функций нет, и получить сразу сквозное упорядочение элементов во всей матрице не представляется возможным. Обозначенная проблема влечет за собой методическую задачу построения алгоритма упорядочения элементов посредством функциональной базы MathCAD, который является удобной и понятной альтернативой их ручной сортировке.

Анализ содержания встроенных матричных функций позволил определить порядок действий по сплошному упорядочению всех элементов двумерного массива, чтобы конечный результат был представлен в исходной форме ‒ в виде двумерной матрицы (рис.1).

Рис. 1. Алгоритм использования встроенных функций MathCAD

Рассмотрим ход реализации предложенного алгоритма. Пусть таблица исходных данных представлена в виде прямоугольной матрицы размерности 10×10 (рис.2).

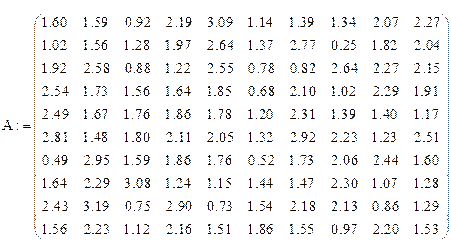Рис. 2. Листинг с исходной матрицей данных

Поскольку операция сортировки элементов может быть применена только к одномерному массиву, то на первом этапе нужно провести ряд действий, которые двумерную матрицу преобразуют в одномерную матрицу-строку, содержащую все исходные данные. Для этого, выделив каждый столбец в виде отдельной матрицы с помощью операции 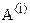, транспонируем получившиеся одномерные матрицы-столбцы операцией 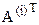и посредством встроенной функции слияния матриц augment(А,B,C,…) составим единую матрицу-строку. Затем, используя встроенную функцию сортировки столбцов rsort (A,i) (здесь i=1 для единственной первой строки), получаем упорядоченный вариационный ряд в виде одномерной матрицы-строки (рис.3).

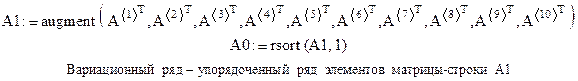Рис. 3. Формирование вариационного ряда в виде матрицы-строки

Важно, что это уже приемлемый предварительный результат, который обучающиеся в зависимости от уровня своей подготовки могут использовать в ручном режиме для дальнейшей работы. В то же время представление упорядоченного множества элементов в таком виде имеет существенный недостаток ‒ использование большого по объему массива данных в виде одной строки становится неудобным при практическом применении. На следующем этапе нужно привести одномерный массив к исходному прямоугольному виду, в котором все элементы имеют сквозную упорядоченность по строкам и столбцам. Для этого выделим из получившейся одномерной матрицы подматрицы-строки В1,В2,В3,…,В10, состоящие из десяти элементов, с помощью встроенной функции submatrix(A0,ir,jr,ic,jc). Здесь для одной и единственной строки ir=jr=1, а номера столбцов соответствуют начальному и последнему порядковому номеру каждого последующего десятка элементов матрицы, начиная с первого (рис.4).

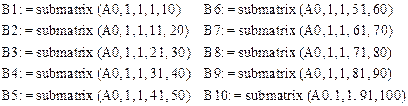Рис. 4. Разбивка вариационного ряда на подматрицы из десяти элементов

Далее, после транспонирования этих матриц в матрицы-столбцы с помощью операций 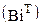, используя повторно функцию сливания матриц augment(А,B,C,…), формируем объединенную двумерную матрицу В исходной размерности 10×10 (рис.5).

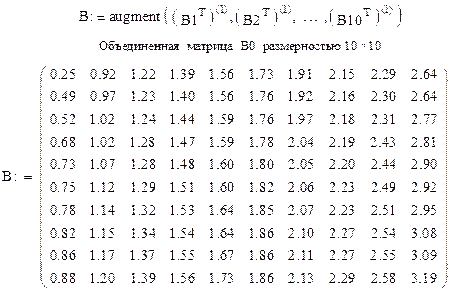Рис. 5. Итоговый вид вариационного ряда в виде матрицы размерности 10×10 (в функции augment часть упорядоченных элементов от 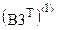до 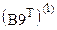не показана)

Видно, что полученный вариационный ряд представлен в удобной для восприятия форме ‒ матрицы с исходной размерностью 10×10 – и имеет сквозное упорядочение элементов по возрастанию их значений сверху вниз, от столбца к столбцу, начиная с наименьшего верхнего левого элемента. В заключение отметим, что вариационный ряд, в котором упорядочение элементов происходит по строкам, также является привычным и удобным для восприятия и практического использования. Такие вариационные ряды могут быть составлены с использованием аналогично построенного алгоритма и тех же встроенных функций. Такую задачу и ее решение при необходимости обучающиеся могут рассмотреть самостоятельно.

Выводы

В процессе освоения учебного материала, который предполагает использование программных математических продуктов в условиях серьезного ограничения учебного времени, с высокой долей вероятности может возникать ситуация непонимания и формального использования обучающимися функциональных возможностей прикладных математических пакетов. В ходе работы было установлено, что оптимальным направлением методической работы является тщательный подбор учебного материала, для сопровождения которого планируется использование программных продуктов. Объем и содержание материала должны определяться в зависимости от степени освоения обучающимися теоретического аппарата и понимания ими основ практических действий.

Подбор сложных задач, с точки зрения уровня реализации программных продуктов, когда использование имеющейся операционной базы не дает возможности напрямую получить требуемый результат, должен предполагать функционально понятную всем обучающимся схему «ручных» действий в рамках их субъективного опыта. Алгоритм использования встроенных математических функций, построенный на основе такой схемы, позволяет дифференцированно подходить к управлению учебной работой в зависимости от уровня математической подготовленности и практических умений обучающихся.