Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

В настоящее время математическая подготовка, статистическая грамотность студентов медицинских вузов является весьма актуальной. Математико-статистические методы широко применяют в диагностических целях, при решении профессионально направленных задач, вопросов, связанных с профессиональной деятельностью будущего врача, а также поиске новых закономерностей, решений для постановки новых предположений (гипотез).

Использование статистических методов в образовательном процессе студентов-медиков является важным инструментом, помогающим им понять и применить свои знания. Статистические методы предоставляют способ измерения, анализа и интерпретации данных, которые могут быть использованы для принятия решений об уходе за пациентами. Изучая статистику, студенты-медики получают ценное представление о том, как различные переменные взаимодействуют друг с другом и как они влияют на результаты лечения пациентов. Это помогает им стать более информированными медицинскими работниками, которые способны ставить более точные диагнозы на основе научно обоснованных исследований, а не только догадок или интуиции. Статистические методы также позволяют студентам-медикам выявлять тенденции в процессах заболевания с течением времени, чтобы они могли соответствующим образом разрабатывать планы лечения [1].

В настоящее время редкий исследователь проводит все вычисления, необходимые для статистического анализа данных, вручную. Большинство используют разнообразные компьютерные пакеты программ. Применение компьютера, с одной стороны, позволяет уйти от рутинной работы и сконцентрировать внимание на собственно творческой составляющей (постановка задач, выбор методов их решения, интерпретация результатов), а с другой – требует определенных знаний и навыков в области компьютерных технологий [2].

Цель исследования – описать методику применения методов математической статистики к обработке данных научно-исследовательской работы студентов медицинских вузов.

Материал и методы исследования

В исследовании Т.Н. Литвиновой, Е.И. Панченко разработан и описан вариативный модуль «Математическая статистика» в рамках блока «Математика» объединенного курса «Физика, математика», а также обозначен прогноз необходимости дополнительного пролонгированного изучения математической статистики студентами-медиками старших курсов. Данный модуль нацелен на формирование у будущих врачей общепрофессиональных, профессиональных компетенций, ориентированных на подготовку выпускника медицинского вуза к научно-исследовательской и медицинской деятельности [3]. В исследовательской работе Л.В. Янцер предлагает методику обучения математической статистики студентов-медиков на основе профессионально ориентированных проблемных ситуаций и внедрения в учебных процесс информационных технологий [4].

Учитывая вышеприведенные методики обучения студентов-медиков, рассмотрим методику применения математико-статистических методов для определения границ доверительного интервала величин динамического и пульсового давления у студентов некоторой группы. Для вычисления параметров будем использовать статистические функции электронной таблицы Excel. Табличный процессор Excel не является профессиональным математическим пакетом, но имеет ряд преимуществ для использования в учебных целях. Во-первых, студенты знакомы с данной программы из школьного курса информатики, во-вторых, эта программа может использоваться в разных режимах – от элементарных табличных вычислений до применения сложных функций и надстроек [5]. Несомненно, табличный процессор Excel – это невероятно мощный инструмент, который может быть использован для улучшения учебного процесса студентов-медиков. Программа Excel позволяет осуществлять сбор и анализ медико-биологических данных, что помогает обучающимся быстро и эффективно понимать сложные концепции. Применяя статистические пакеты Microsoft Excel, студенты-медики могут лучше визуализировать свои данные, чтобы получить более глубокое понимание изучаемого материала. Также данная программа дает возможность студентам медицинских специальностей создавать модели, которые упорядоченно отображают важную информацию, такую как истории болезни пациентов или результаты лабораторных исследований. Благодаря этим визуализациям им становится легче выявлять закономерности в данных и делать значимые выводы на основе этих данных.

Результаты исследования и их обсуждение

Рассмотрим методику (методические пути, методические основы) преподавания дисциплины «Применение метода математической статистики к обработке данных научно-исследовательской работы» в учебном процессе лечебного факультета Астраханского ГМУ.

Согласно учебному плану данная дисциплина изучается на шестом семестре третьего курса специальности «Лечебное дело», что, в свою очередь, имеет некоторые преимущества. Во-первых, студенты третьего курса более осознанно подходят к процессу обучения, и у них уже формируется некоторая профессиональная направленность; во-вторых, на лабораторных занятиях по данной дисциплине они решают статистические задачи с использованием информационных технологий; в-третьих, это цикловые занятия, когда на процесс обучения отводится определенный отрезок времени, в течение которого при ежедневных занятиях студенты медицинского вуза должны освоить данную дисциплину.

В процессе освоения дисциплины «Применение метода математической статистики к обработке данных научно-исследовательской работы» у студентов медицинских специальностей должны быть сформированы следующие компетенции:

– универсальные компетенции УК-2: «Способен управлять проектом на всех этапах его жизненного цикла» – студент должен уметь проверять, анализировать проектную документацию, рассчитывать качественные и количественные показатели проектной работы с применением современных средств информационных технологий;

– профессиональные компетенции ПК-7: «Способность к анализу научной литературы и официальных статистических обзоров, участию в проведении статистического анализа и публичному представлению полученных результатов» – студент должен владеть алгоритмом и методиками проведения научно-практических исследований с применением современных средств информационных технологий и уметь проводить анализ научной литературы и электронных научных баз.

Основные разделы данной дисциплины: краткий курс теории вероятностей, элементы математической статистики, методы статистического анализа медицинских данных, анализ данных с помощью табличного процессора Excel.

Согласно учебному плану на освоение дисциплине студентам отводится всего 72 часа, из них на аудиторную работу – 48 часов, это предполагает 16 часов лекционных занятий и 32 часа лабораторных занятий, на самостоятельную работу студентам выделяется 24 часа.

Приведем перечень разработанных лабораторных работ для реализации практикума по дисциплине «Применение метода математической статистики к обработке данных научно-исследовательской работы»:

Лабораторная работа № 1 «Моделирование случайных величин».

Лабораторная работа № 2 «Графическое представление статистического распределения».

Лабораторная работа № 3 «Точечное и интервальное оценивание параметров распределения».

Лабораторная работа № 4 «Проверка статистических гипотез».

Лабораторная работа № 5 «Проверка гипотез о равенстве дисперсий и математических ожиданий».

Лабораторная работа № 6 «Статистическое исследование зависимостей».

Лабораторная работа № 7 «Создание математических моделей медико-биологических систем».

В качестве примера остановимся на выполнении студентами-медиками лабораторной работы № 3 «Точечное и интервальное оценивание параметров распределения».

Целью данной лабораторной работы является изучение математико-статистических методов медико-биологических данных, которые подчиняются нормальному закону распределения случайных величин.

Требуется определить доверительные границы среднего уровня величин динамического и пульсового давления у студентов медицинского вуза с 95%-ной вероятностью безошибочного прогноза.

В начале лабораторного практикума студенты-медики знакомятся с теоретической информацией, необходимой для применения ее на практике.

Разница между систолическим и диастолическим давлениями, известная как пульсовое давление, или среднее артериальное давление, отражает, с какой силой сердце выталкивает кровь при каждом ударе. Пульсовое давление вычисляется по формуле: .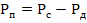

Студентам важно понять концепцию среднего динамического давления как меры энергии для непрерывного кровотока. Среднее динамическое давление можно использовать для расчета всех переменных, связанных с сердечным циклом, и соотнесенных с ними циклических изменений состояния артериальных сосудов и периферического сосудистого сопротивления. Расчет среднего динамического давления можно приближенно рассчитать по формуле Хикаама: 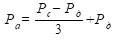, где Ра – среднее динамическое давление, Рс – систолическое давление; Рд – диастолическое давление.

Эта формула помогает нам получить приблизительное значение средней силы, действующей на сосуды в течение определенного периода, в данном случае одного сердечного цикла, которое затем используется в качестве показателя общего состояния здоровья сердечно-сосудистой системы. Знание того, как точно рассчитать среднее динамическое давление, дает нам ценные сведения о функционировании собственного организма, к которым мы, возможно, не имели бы доступа.

После изложения преподавателем теоретического материала студенты приступают к выполнению лабораторной работы, строго придерживаясь разработанного пошагового алгоритма.

1. Студенты определяют величины артериального давления, измерения повторяют по три раза, полученными результатами обмениваются друг с другом. Будущим врачам стоит напомнить, что в клинике в историю болезни записывают только одно значение артериального давления из трех – минимальное. Полученные при измерении артериального давления данные студенты записывают на лист Excel, числовые величины располагают либо по строчкам, либо по столбцам.

2. Используя вышеприведенную формулу Хикама, вычисляют величины динамического и пульсового давления. Для этого студенты ставят курсор в ячейку С3 и вводят формулу вычисления динамического давления: =((А3-В3)/3)+В3, затем автозаполняют данную формулу на С3-С15, перемещая нижний правый угол С3 до ячейки С15. Для вычисления пульсового давления студенты ставят курсор в ячейку D3, вводя формулу: =А3-В3, аналогично перемещая нижний правый угол D3 до ячейки D15 автозаполняют формулу на ячейки D3 по D15.

3. Для того чтобы воспользоваться статистической функцией определения доверительного интервала, необходимо рассчитать среднее арифметическое значение, стандартное отклонение величин динамического и пульсового давления. Для вычисления среднего арифметического значения динамического и пульсового давления студенты используют формулу точечного оценивания параметра распределения:

а) вычисление среднего значения величин динамического давления: =СРЗНАЧ(C3:C15);

б) вычисление среднего значения величин пульсового давления: =СРЗНАЧ(D3:D15).

Для вычисления стандартного отклонения величин динамического и пульсового давления студенты используют формулу точечного оценивания параметра распределения:

а) вычисление стандартного отклонения величин динамического давления: =СТАНДОТКЛОН(C3:C15);

б) вычисление стандартного отклонения величин пульсового давления: =СТАНДОТКЛОН(C3:C15).

4. По полученным данным электронная таблица Excel, содержащая встроенные статистические функции, позволяет быстро определить границы доверительного интервала исследуемой величины. Для этого используют функцию из категории «Статистические» «ДОВЕРИТ» с тремя параметрами: «Альфа» – уровень значимости 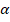=1 – p , «Станд_откл» – среднеквадратическое отклонение S, «Размер» – объем выборки п. Данные параметры приведены на рисунке 1.

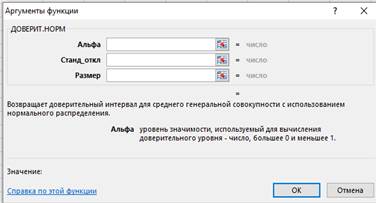
Рис. 1. Статистическая функция для вычисления доверительного интервала

5. Вычисление доверительных границ величин динамического давления:

Левая граница: =B19-ДОВЕРИТ(B18;B20;15)

Правая граница: =B19+ДОВЕРИТ(B18;B20;15)

Вычисление доверительных границ величин пульсового давления:

Левая граница: =D19-ДОВЕРИТ(B18;D20;B17)

Правая граница: =D19+ДОВЕРИТ(B18;D20;B17)

2. Проведя все необходимые вычисления, обучающиеся интерпретируют полученные результаты исследования и в заключение отмечают: установлено с вероятностью безошибочного прогноза: 95%-ный средний уровень динамического давления в генеральной совокупности находится в пределах от 88 мм рт. ст. до 93 мм рт. ст.; аналогично и для пульсового давления студенты определяют границы доверительного интервала от 46 мм рт. ст. до 52 мм рт. ст.

Доверительный интервал динамического и пульсового давления является важным показателем при определении общего состояния сердечно-сосудистой системы пациента. Он дает представление о функционировании сердца, а также о любых потенциальных проблемах, которые могут присутствовать. Определение этого доверительного интервала требует тщательного рассмотрения и анализа для обеспечения точности, что может помочь врачам принимать более обоснованные решения относительно планов ухода за своими пациентами. Совместное использование этих двух измерений позволяет клиницистам рассчитать доверительный интервал между ними и предоставляет ценную информацию о том, насколько точно они отражают друг друга с течением времени и имеются ли какие-либо отклонения, требующие дальнейшего обследования или соответствующего изучения вариантов лечения. Окончательно электронная таблица Excel представлена на рисунке 2.

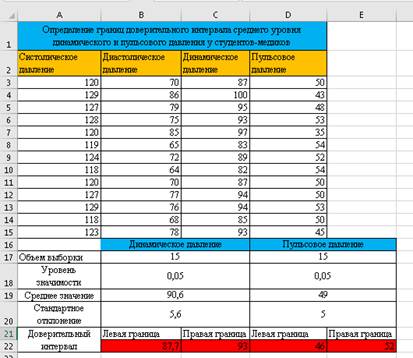
Рис. 2. Окончательная таблица вычисления доверительного интервала

Заключение

Проведение лабораторного практикума на основе описанной выше методики применения методов математической статистики при определении границ доверительного интервала величин динамического и пульсового давления имеет ряд преимуществ. Во-первых, оно развивает познавательную деятельность студентов медицинских специальностей; во-вторых, применение информационных технологий формирует и развивает алгоритмическое мышление студентов-медиков, освобождая их от рутинных вычислений; в-третьих, формирует навыки самостоятельной научно-исследовательской деятельности будущего врача. В заключение следует отметить, что математика является бесценным инструментом для студентов, обучающихся в медицинских университетах, которые хотят получить дальнейшее представление о том, как делать более точные прогнозы в своей профессиональной деятельности.