Качество – это степень соответствия присущих характеристик требованиям [1]. Любое отклонение рабочей характеристики от заданного значения приносит потери потребителю, которые могут повлечь за собой финансовый или физический ущерб.
Предлагается произвести анализ размера потерь потребителя с помощью модели организации (рисунок 1), полученной путём доработки графической модели, приведённой в [3].
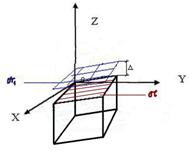
Рисунок 1. Модель организации
Пусть 0X – ось времени, 0Y – ось внутренних факторов, влияющих на внутреннюю среду организации, 0Z – ось внешних факторов, рассмотренных в [2].
Куб, построенный в трёхмерной системе координат, иллюстрирует положение компании на рынке.
Рассмотрим частный случай построенной модели с точки зрения философии Тагути.
Плоскость π символизирует возможности организации, максимальный уровень технического развития, который имеет компания.
Плоскость π1 характеризует уровень современных требований потребителей к качеству, возможно невысказанных (для выпускаемой компанией продукции).
Расстояние между плоскостями π и π1 обозначим через Δ. Оно характеризует разницу между возможностями производителей и потребностями потребителей в данный момент.
В плоскости Y0Z (рисунок 2) прямые р (совпадает с осью 0Y) и р1 символизируют линии прохождения плоскостей π и π1 через рассматриваемую плоскость.
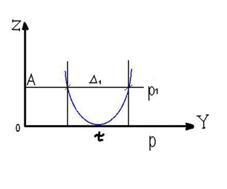
Рисунок 2. Плоскость Y0Z.
Пусть 0Z – ось, которая характеризует потери потребителя, которые он может понести вследствие того, что 
. Ось 0Y – ось значений какой-либо непрерывно измеряющейся рабочей характеристики изделия. Заданное значение которой обозначим τ. Положим, что 
- заданный заказчиком допустимый интервал значений рабочей характеристики (Δ1).
Пусть Z(Y) – функция потерь (в условных единицах) некоторого заказчика в произвольный момент времени в процессе эксплуатации при неотработанном ресурсе вследствие отклонения Y от τ.
Обычно трудно определить действительную форму функции Z(Y). Часто квадратичная аппроксимация Z(Y) адекватно представляет экономические потери [4].
Простейшей квадратичной функцией потерь считается 
, где κ – некоторая константа.
Неизвестную константу можно определить при известном значении функции Z(Y) для конкретного значения аргумента Y.
Допустим, что при выходе параметра Y за установленные пределы Δ1, затраты на ремонт и списание продукта составляют А условных единиц.
Тогда 
и 
.
Средняя величина потерь потребителя, обусловленных отклонением рабочей характеристики, получается статистическим усреднением функции потерь.
В случае квадратичной функции потерь среднее значение потерь пропорционально среднему квадрату ошибки Y по отношению к заданной величине τ. Поэтому основным показателем изменчивости является квадрат ошибки, а не дисперсия.
Рассмотренный случай может быть распространён на множество ситуаций.
Например, если Y – это содержание загрязнений с заданным значением – нуль, то получаем случай «чем меньше, тем лучше».
Если же Y характеризует прочность, тогда имеет место случай «чем больше, тем лучше».
Кроме того, концепция усреднённой потери, обусловленной отклонением рабочей характеристики, может применяться для описания возможностей технологических процессов.
В связи с важностью вышесказанного, следует отметить, что при планировании мероприятий по повышению качества необходимо учитывать вопросы непрерывного уменьшения отклонений рабочих характеристик продукции от заданных величин.
СПИСОК ЛИТЕРАТУРЫ
1. ГОСТ Р ИСО 9000-2001 Системы менеджмента качества. Основные положения и словарь.
2 Гимпельсон Л.В. Иллюстрация качества менеджмента на модели организации//Фундаментальные исследования. – 2006. – № 1. – с. 54-55.
3. Тарушкин В. О современной парадигме диссертационных работ применительно к проблемам агропромышленного комплекса России //Стандарты и качество. – 2003. – № 4. с. 28-33.
4. Философия качества по Тагути. Серия «Всё о качестве. Зарубежный опыт». Выпуск 6, 2000/Пер. с англ. – М.: НТК «Трек», 2000. – 17 с., ил.
Библиографическая ссылка
Гимпельсон Л.В. ОЦЕНКА ПОТЕРЬ ПОТРЕБИТЕЛЕЙ // Современные проблемы науки и образования. 2006. № 3. ;URL: https://science-education.ru/ru/article/view?id=322 (дата обращения: 03.04.2025).